쇄파가 수중 수평판의 고립파 제어에 미치는 영향
Effects of Wave Breaking over Submerged Horizontal Plate on Solitary Wave Control
Article information
Trans Abstract
A numerical analysis was performed to analyze the solitary wave control mechanism of a submerged horizontal plate (SHP). A two-dimensional numerical wave tank (NWT), which uses a wave generation method that generates a stable solitary wave, was employed for the numerical analysis. To verify the effectiveness of the NWT, the waveform measured around the SHP was compared to the calculated waveform. Moreover, the approximate and the calculated waveforms were compared in order to examine whether the solitary wave was stably generated. The results of comparison and verification showed that the deformation of the solitary wave by SHP was reproduced with high accuracy in the calculation, while the calculated waveform of NWT also showed a high degree of matching with the approximate waveform. The solitary wave breaking on the SHP satisfied the existing threshold condition A0/hc > 0.827-0.833, but breaking did not occur even under the condition A0/hc=1.2 when the width of the SHP was small. Accordingly, the wave height attenuation of the solitary wave occurred rapidly in a breaking condition. In a non-breaking condition, the energy gradually decreased due to the vorticity and turbulence around the boundary of the SHP, resulting in a gradual attenuation of the solitary wave.
1. 서 론
최근 국내에서는 미관상의 이유로 잠제가 많이 설치되고 있다. 그러나 잠제 배후의 수위상승은 이안류를 발생시킬 뿐 아니라(Hur et al., 2019a), 조위차가 큰 해역에는 설치가 사실상 불가능하다(Hur et al., 2019b). 이 문제들을 해결하기 위한 신형식 잠제가 개발되기도 하였으나(Hur et al., 2017; Hur et al., 2019c; Lee et al., 2019a), 현장에 적용하기 위해서는 극복해야 할 문제가 많다.
수중 수평판(SHP, Submerged horizontal plate)은 위⋅아래로 자유롭게 흐름이 통과할 수 있는 구조이다. SHP는 해빈류, 조류, 해류와 같은 흐름은 큰 저항 없이 흘려보내고, 파랑만 제어할 수 있다는 의미이기도 하다. 또한, 흐름이 원활한 SHP는 잠제에서 발생하는 배후 수위상승, 이안류 등의 문제에 대해 자유롭다. 그러한 까닭에 Ijima et al.(1970)는 SHP의 방파제 사용 가능성을 언급하였다.
과거에는 주로 포텐셜 이론에 기초해 수평판에 의한 파랑의 반사계수와 전달계수를 해석하였다. Siew and Hurley (1977)는 일정한 마루수심을 가진 SHP, Linton(2001)는 수면 위에 설치된 수평판에 의한 파랑 반사와 전달에 관한 해석해를 구하였다. Wu et al.(1998)는 SHP의 유공이 반사파를 크게 줄일 수 있음을 해석적 연구를 통해 밝혀내었다. 그리고 Patarapanich and Cheong(1989)는 파동수조에서 다양한 SHP 폭과 마루수심을 고려한 실험을 수행하였다. Neelamani and Gayathri(2006)는 규칙/불규칙 파동장에서 이중 불투과성 수평판에 의한 반사계수와 전달계수를 측정하였다. Cho and Kim(2008)은 유공 SHP의 유공율과 기울기에 따른 소파 성능을 실험 및 해석이론을 통해 조사하였다. 이 실험적 연구들에서 밝혀진 몇 가지 주요 사항은 다음과 같다. 파랑 전달율을 줄이기 위해서는 SHP의 폭은 입사파장의 0.5-0.7배, 마루수심은 쇄파를 유도할 수 있는 깊이가 바람직하다(Patarapanich and Cheong, 1989). 이중 SHP의 간격을 적절히 조절하면, 단일 SHP보다 파랑제어 성능이 향상된다(Neelamani and Gayathri, 2006). 유공 SHP는 유공율이 0.1, 기울기가 10°일 때 소파성능이 가장 우수하다(Cho and Kim, 2008). 그 밖에 경계요소법(Cho et al., 2013)과 유한차분법(Kweon et al., 2014)을 이용하여 SHP의 수리성능을 분석하기도 하였다.
2011년 동일본 대지진에 의한 쓰나미는 하구지역 교량에 큰 피해를 주었다. 이를 계기로 고립파-SHP 상호작용에 관한 연구들이 활발히 진행되고 있다. 고립파 내습시에 수평판(Seiffert et al., 2014) 교량(Hayatdavoodi et al., 2014)에 작용하는 하중을 실험과 OpenFoam을 이용한 수치모의에서 측정하였다. Lo and Liu(2014)는 PIV(Particle image velocimetry)와 COBRAS(Cornell breaking waves and structures) 모델(Lin and Liu, 1998)의 결과로부터 SHP 주변의 유동과 와동구조를 조사하였다. 또한 GN(Green-Naghdi) 방정식, CIP(Constrained interpolation profile) 기반의 다상류 해석모델, MPS(Moving particle semi-implicit)법을 적용해 고립파-SHP 상호간섭에 따른 수리특성을 분석하였다(Hayatdavoodi et al., 2017; You et al., 2019; Xu et al., 2019).
SHP의 소파성능은 수중에 설치되는 잠제와 같이 강제 쇄파 유도에 달려 있다. 이에 Yu et al.(1995)은 부분 중복파 쇄파에 관한 경험식(Iwata and Kiyono, 1983)으로부터 SHP상에서의 쇄파 한계조건를 제안하였다. 일반적으로 쇄파 한계에 대해서는 규칙파 실험을 통해 제안된 Goda(1970)의 조건식이 대표적이나, 고립파의 쇄파 한계와는 차이가 있다. 고립파의 쇄파 한계에 대해서는 Yamada(1957)가 파고와 수심 비 0.827, Witting(1975)과 Wu et al.(2005)이 0.833을 제안하였다. 따라서 SHP 상에서 고립파의 쇄파 한계조건뿐 아니라, 쇄파 발생 유무에 따른 SHP의 고립파 제어효과에 관한 논의가 필요하다.
본 연구에서는 SHP 상에서 고립파의 쇄파 발생조건을 조사하고, 쇄파 유무가 고립파의 반사, 전달, 에너지 감쇠에 미치는 영향을 분석한다. 이를 위해 다양한 연구를 통해 신뢰도가 확인된 Navier-Stokes(N-S) 방정식 기반의 Numerical wave tank(NWT; Lee et al., 2016a)를 이용한다. 또한, SHP를 통과하는 고립파의 파동장, 유동장, 와동장, 난류에너지를 도시하여 고립파의 에너지소산 메커니즘을 분석한다.
2. 수치모델
본 연구에서는 수중 수평판의 파랑제어 성능을 분석하기 위한 수치해석을 수행한다. 수치해석에서는 PBM(Porous body model)을 적용한 수정된 N-S 방정식 모델(Hur et al., 2011)에 기초하여 Lee et al.(2016a)이 개발한 2차원 NWT를 이용한다. 이 NWT의 정확도와 안정성은 기존 수치연구(Lee et al., 2016b; Lee et al., 2018; Lee et al., 2019b; Lee et al., 2019c)에서 여러 검증을 통해 확인된 바 있다.
2.1 지배방정식
NWT의 지배방정식은 비압축성⋅점성유체에서 안정적으로 파랑을 생성할 수 있게 소스항이 추가된 연속방정식, PBM에 기초하여 수정된 2차원 N-S 운동량 방정식으로 구성된다.
여기서 ui는 x, z방향의 유속, q*는 소스의 유량밀도, γv는 체적 공극률, γi는 x, z방향의 면적 공극률, t는 시간, ρ는 유체 밀도, p는 압력, νT는 유체의 동점성계수(ν)와 와동점성계수(νt)의 합, Dij는 변형률속도텐서, Sij는 Continuum surface force(CSF) 모델(Brackbill et al., 1992)에 기초한 표면장력항, Qi는 파랑 생성항, Ri는 투과매체의 유체저항항, gi는 중력가속도항, Ei는 스폰지층의 에너지 감쇠항이다.
비압축성⋅점성유체에 기초한 연속방정식에 PBM 개념을 적용한 Volume of fluid(VOF) (Hirt and Nichols, 1981)함수는 다음과 같다.
여기서 F는 각 격자에서 유체 체적비이고, F = 1는 물만 존재하는 격자, F = 0는 공기만 존재하는 격자, 0 < F < 1는 자유수면 격자를 나타낸다.
2.2 고립파 조파방법
NWT에서 고립파를 안정적으로 생성하기 위해 Brorsen and Larsen(1987)의 무반사 조파강도식에 근거를 둔 Lee et al.(2016c)의 방법을 이용한다. 그리고 입사파와 반사파가 중첩될 경우, 목표파형을 정확하게 조파하기가 어렵다. 이에 강도조절을 통해 안정적 파랑생성이 가능한 Ohyama and Nadaoka(1991)의 빙법을 적용한다.
여기서 V0는 근사이론에 의한 수평유속성분, 2는 NWT에서 파랑이 양방향으로 전파됨에 따른 상수값, Sw는 조파 강도(= (η0 + h)/(ηs + h); η0는 근사파형, ηs는 생성파형, h는 수심)를 각각 나타낸다.
Lee et al.(2016)은 Dean and Dalrymple(1984)의 근사식 (5)-(6)에 기초한 고립파를 NWT에서 안정적으로 조파하였다. 고립파의 시간파형과 유속의 이론식은 다음과 같다.
여기서 A0는 고립파의 진폭, C는 파속(=
2.3 NWT의 검증
Lo and Liu(2014)는 길이 32m, 폭 0.6m의 2차원 파동수조에서 SPH를 적용한 고립파 실험을 수행하였다. NWT의 유효성 및 수치결과의 타당성을 입증하기 위하여 Lo and Liu(2014)의 수리모형실험과 비교⋅검토한다. 이 검증에서는 Fig. 1처럼 실험수조의 양쪽에 설치된 조파기와 1:20 경사면을 제외한 길이 22m를 고려한 NWT를 구성한다. 그리고 실험과 비교⋅검증을 위해 NWT에 설치된 5개 파고계로 부터 계산된 시간파형을 얻는다.
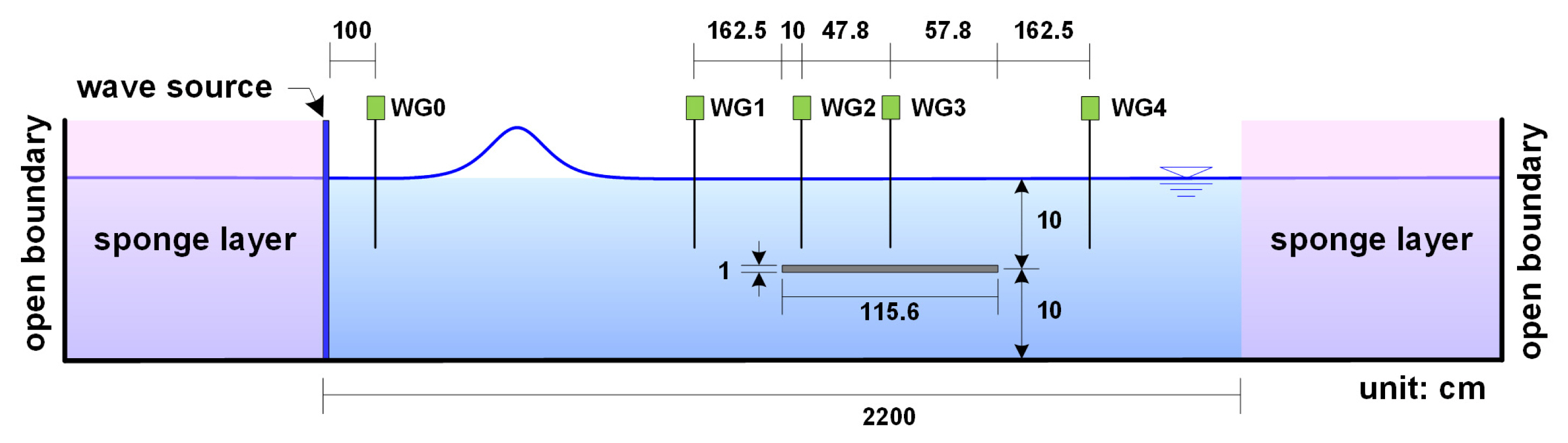
Schematic diagram of a NWT based on Lo and Liu (2014)’s experimental one
Fig. 2는 Lo and Liu(2014)의 실험수조에서 생성된 고립파의 입사파형과 NWT의 WG0으로부터 얻은 계산파형을 비교하여 나타낸 것이다. NWT의 계산파형이 실험수조의 측정파형보다 조금 넓게 분포하나, 고립파의 진폭을 비롯한 시간파형의 전반적 분포를 잘 재현한다.
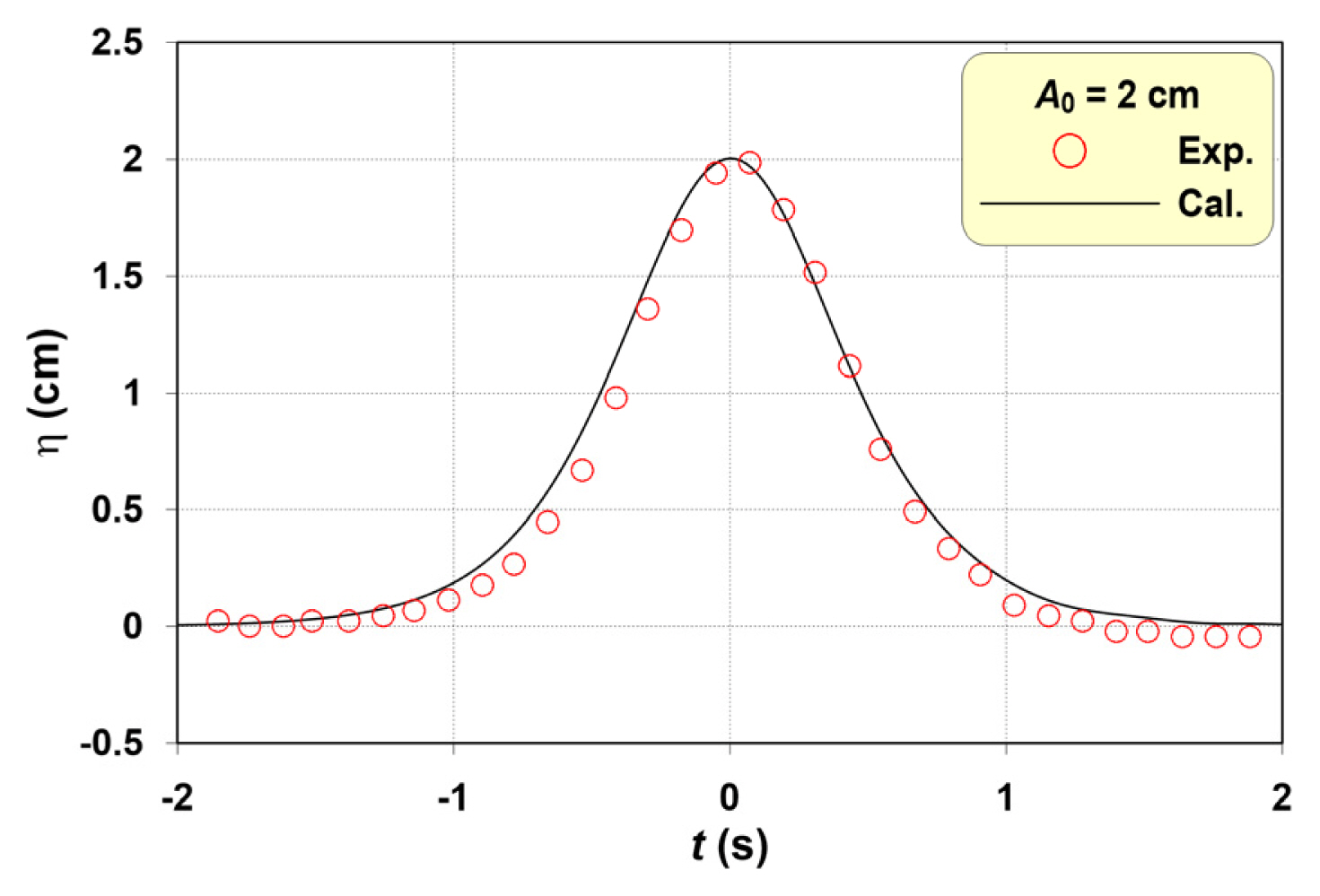
Comparison of incident waveform with the measured free surface elevation in the experimental wave flume
Fig. 3은 NWT에서 계산된 수면변위를 Lo and Liu(2014)의 실험값과 비교한 것으로 (a) WG1은 SHP 전면, (b) WG2와 (c) WG3는 SHP 위, (d) WG4는 SHP 배후의 수면파형을 각각 나타낸다. 고립파가 SHP를 통과하면서 전면의 WG1에서는 입사파형과 반사파형, WG2와 WG3에서는 파형변형 그리고 WG4의 전달파형을 각각 확인할 수 있다. 이 같은 일련의 고립파 전파과정에서 계산값과 실험값을 비교하면, 높은 일치도를 나타낸다.
Comparison between the measured and calculated free surface elevation at offshore (left) and onshore (right)
이로써 NWT에 도입한 고립파 조파방법의 타당성 및 유효성뿐 아니라, 본 연구의 수치해석결과에 대한 신뢰도가 어느 정도 검증되었다고 판단된다.
2.4 NWT의 구성
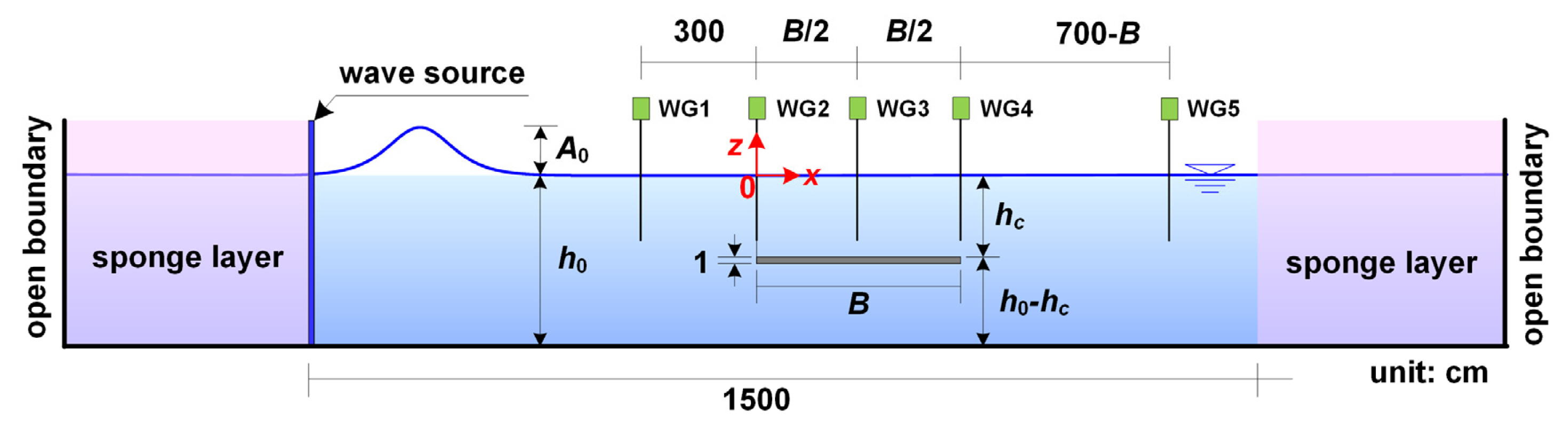
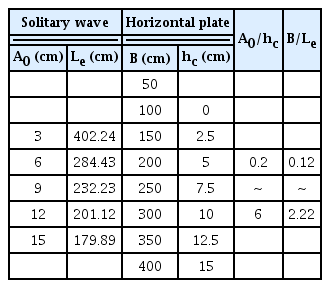
본 연구에서는 SHP의 고립파 제어기능을 분석할 목적으로 Fig. 4와 같은 NWT를 구성한다. 수치해석조건은 Table 1과 같으며, 고립파의 입사진폭(A0)는 3-15cm이고, 두께 1cm의 SHP 폭(B)은 50-400cm, 마루수심(hc)은 0-15cm이다. 따라서 hc=0cm를 제외하고, 입사진폭과 마루수심과의 비(A0/hc)는 0.2-6, SHP 폭과 고립파의 유효파장과의 비(B/Le)는 0.12-2.22이다. 여기서 유효파장은 고립파의 95% 체적에 해당하는 값으로 Dean and Dalrymple(1984)가 제안한 방법으로 산정하였다.
Definition sketch of a NWT including a SHP used in this study
Initial and incident conditions used for numerical simulations
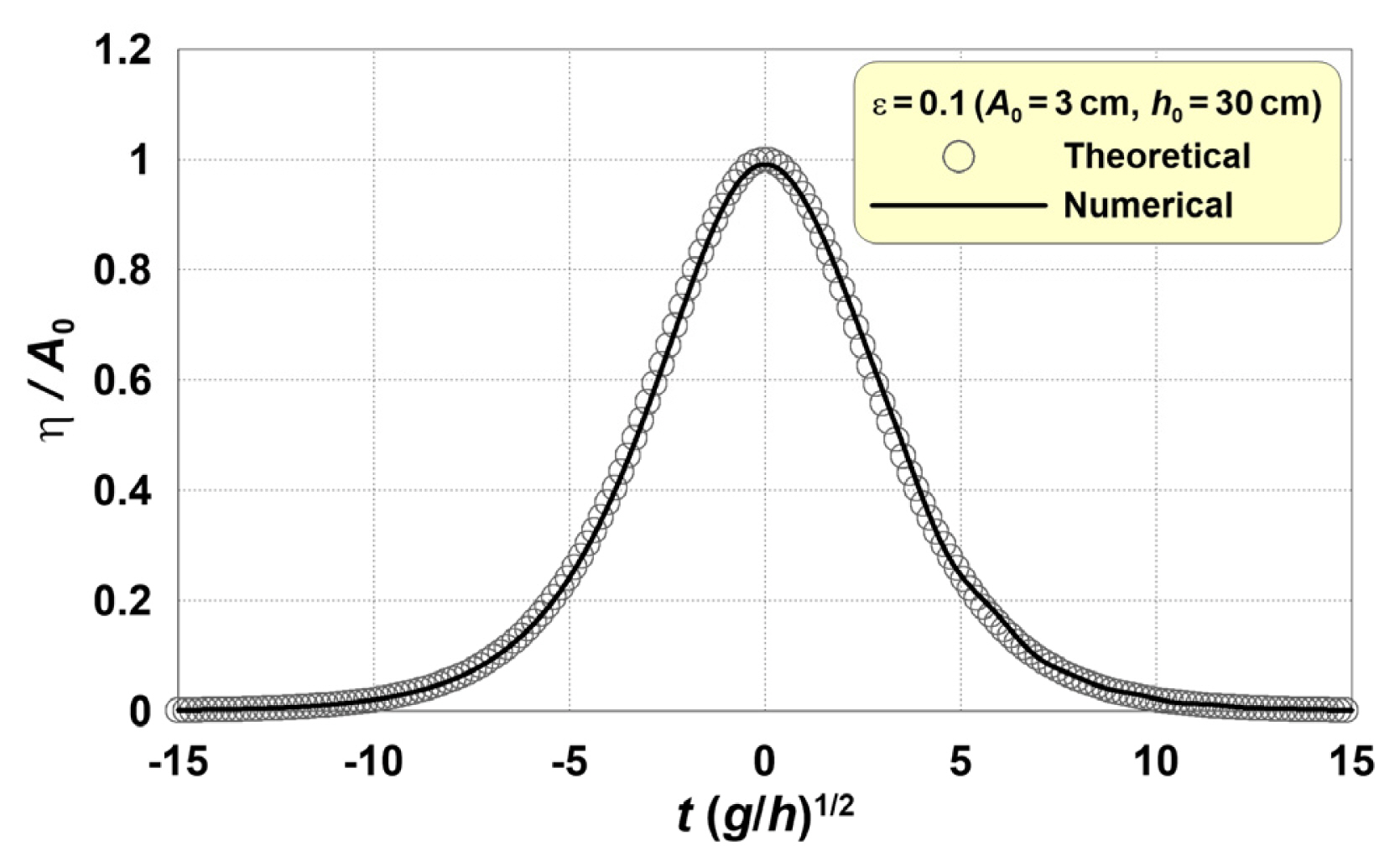
NWT에서는 Dean and Dalrymple(1984)의 근사이론에 기초하여 고립파를 생성한다. 고립파 조파의 신뢰성을 확인하기 위해 Fig. 5에 NWT의 수치모의를 통해 얻은 수면변위와 근사이론의 시간파형을 비교하여 나타낸다. Fig. 5로부터 근사파형과 계산파형이 거의 일치하는 것을 확인할 수 있다. 도시하지 않은 나머지 입사진폭에서도 유사한 결과를 나타낸다. 따라서 본 연구에서 이용하는 NWT와 조파방법이 고립파의 전파해석에 적합한 것으로 판단된다.
Comparison of incident waveform with the theoretical value at wave source
3. 수치모의결과
3.1 유동/와동장
Fig. 6에는 고립파가 통과하면서 SHP의 시작지점, 중앙, 끝지점에 위치한 WG1, WG2, W3에서 최대수위가 발생하는 시점의 유속과 와도의 공간분포를 각각 나타낸다. 최대 수위 발생지점(WG1, WG2, W3)가 위치한 지점)은 (a)는 x/Le=0, (b)는 x/Le=0.35, (c)는 x/Le=0.7을 기준으로 한다. Fig. 6에서 벡터는 수평과 수직유속의 합벡터이고, 고립파의 파속으로 무차원 하였다. 그리고 색으로 표현된 와도(ω)는 Raffel et al.(2007)의방법으로 산정하였으며, 음의 값은 시계방향, 양의 값은 반시계 방향의 와도를 각각 의미한다.
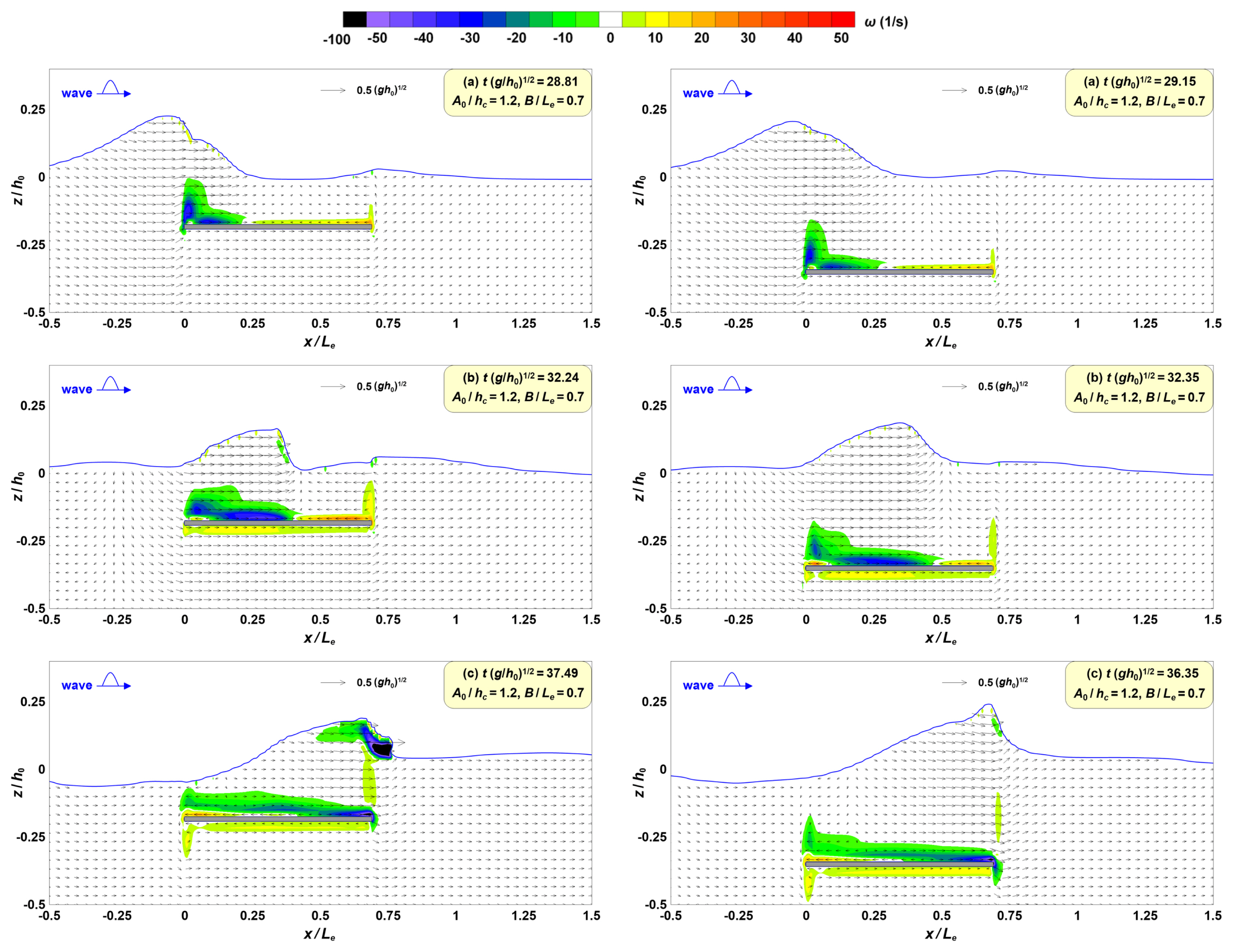
Spatial distribution of velocity and vorticity due to the propagation of a solitary wave for ɛ = 0.2, B/Le = 0.7 (left: A0/hc = 1.2, right: A0/hc = 0.4)
Fig. 6에서 A0/hc=1.2 조건(왼쪽 그림)에서는 쇄파가 발생하고, A0/hc=0.4 조건(오른쪽 그림)에서는 쇄파가 나타나지 않음을 알 수 있다. 그리고 고립파의 전파과정에서 SHP 상⋅하 유속의 위상차로 인해 와도가 형성되고, 특히 파봉 작용 하에서 SHP의 상부, 쇄파로 인한 수면부근의 와도가 강하게 발생한다.
3.2 난류에너지
Fig. 7은 Fig. 6처럼 고립파 전파과정에서 SHP의 시작지점, 중앙, 끝지점에서 최대수위가 발생하는 시점의 유속과 난류에너지(k)의 공간분포를 각각 나타낸 것이다. Fig. 6에 색으로 표현된 k는 계산격자 스케일과 아격자 스케일의 난류 에너지의 합이며, Christensen(2006)의 방법으로 추정하였다.
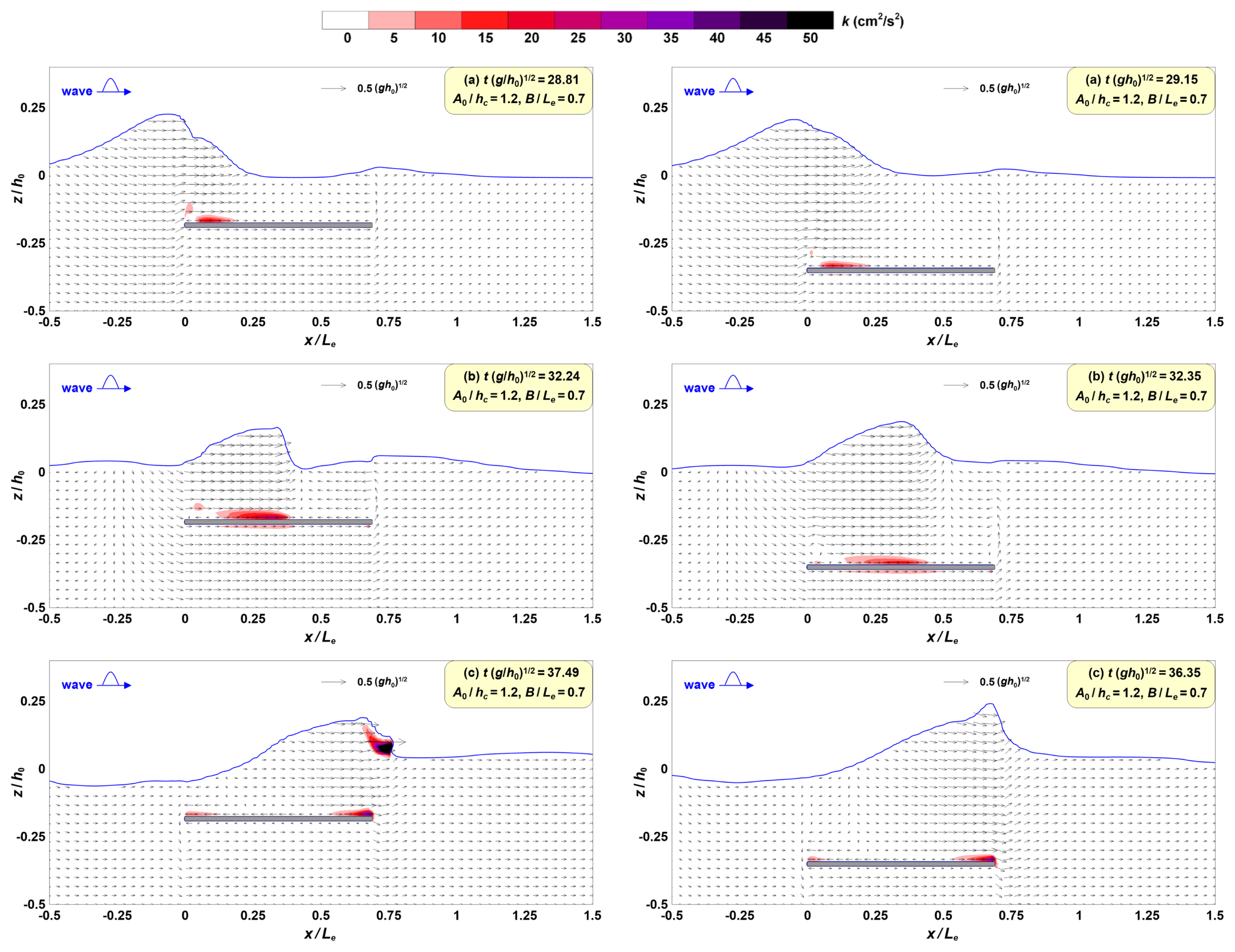
Spatial distribution of velocity and turbulent kinetic energy due to the propagation of a solitary wave for ɛ = 0.2, B/Le = 0.7 (left: A0/hc = 1.2, right: A0/hc = 0.4)
파봉이 통과할 때, SHP의 상부에 k가 강하게 나타나는 것을 Fig. 7에서 확인할 수 있다. 특히, A0/hc=1.2조건(왼쪽 그림)에서 쇄파 발생 시에 자유수면 뿐만 아니라, SHP 표면에도 강한 k가 형성된다.
SHP의 유체저항에 기인한 유동변화는 와도를 발생시키고, SHP 경계에서 발생하는 난류는 고립파의 에너지감쇠를 유발한다. 또한, 쇄파가 발생하는 경우에 나타나는 자유수면 부근의 강한 와도와 난류에너지는 파랑에너지를 더욱 감쇠시킬 것이다.
3.3 쇄파특성
SHP를 통과하는 고립파의 변형 및 쇄파 유무를 확인하기 위하여 Fig. 8과 Fig. 9에 자유수면의 시⋅공간분포를 각각 나타낸다. Fig. 8은 B/Le=0.7 고정조건에서 A0/hc, Fig. 9는 A0/hc=1.2 고정조건에서 B/Le에 따른 파동 변화를 비교한다. Fig. 8과 Fig. 9에 도시된 자유수면의 시간간격은 t(g/h0)1/2=2.86이다.
Temporal and spatial distribution of free surface elevation by solitary wave propagating over a SHP for ɛ = 0.2, B/Le = 0.7: (a) A0/hc = 1.2; (b) A0/hc = 0.4
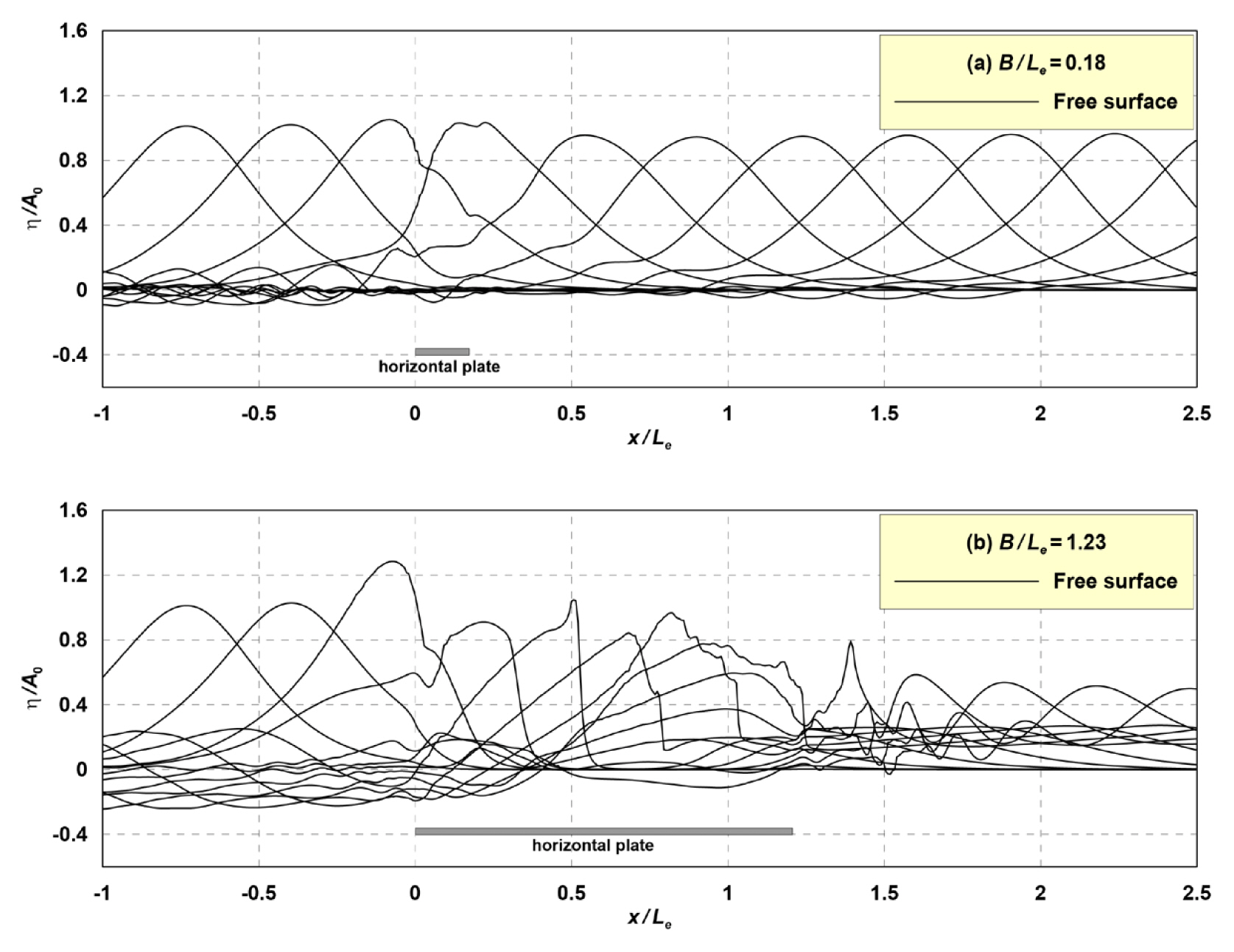
Temporal and spatial distribution of free surface elevation by a solitary wave passing over a SHP for ɛ = 0.2, A0/hc = 1.2: (a) B/Le = 0.18; (b) B/Le = 1.23
Fig. 8의 (a) A0/hc=1.2 조건에서는 쇄파가 발생하고, (b) A0/hc=0.4 조건에서는 쇄파가 발생하지 않는다. 이것은 기존 연구의 고립파 쇄파기준 A0/hc>0.827-0.833에 부합하는 결과이기도 하다. 또한, 쇄파가 발생하지 않는 (b) A0/hc=0.4 조건에서도 고립파-SHP 상호간섭에 의한 에너지 소산으로 파고감쇠와 파형변형이 나타난다.
한편, Fig. 9에서 쇄파가 발생한 A0/hc=1.2 조건에서 SHP폭이 작은 (a) B/Le=0.18 조건에서는 쇄파가 발생하지 않는다. 그리고 SHP 폭이 긴 (b) B/Le=1.23에서는 강한 쇄파와 더불어 파고감쇠가 크게 일어난다.
SHP 상에서 고립파의 쇄파 발생조건을 Table 2에 나타낸다. Table 2에서 A0/hc에 따른 결과는 B/Le=0.7, B/Le에 따른 결과는 A0/hc=1.2가 각각 고정된 조건이다. 여기서 ‘×’는 해당하는 모든 계산조건에서 쇄파가 발생하지 않았고, ‘○’는 모두 쇄파가 발생하였다. 이 결과는 고립파 쇄파기준 A0/hc>0.827-0.833에 대체적으로 부합하나, SHP 폭이 작은 경우에는 A0/hc>0.827-0.833 조건에서도 쇄파가 발생하지 않았다.
Critical conditions for wave breaking
앞서 논의한 유동, 와동, 난류특성과 함께 살펴보면, SHP로 인해 쇄파가 발생하고, 그 영향으로 생성된 강한 와도, 난류가 고립파를 감쇠시킨다. 그리고 쇄파가 발생하지 않더라도 SHP 주변에 형성되는 와도와 난류가 고립파의 에너지를 서서히 감쇠시킨다.
3.4 파고분포
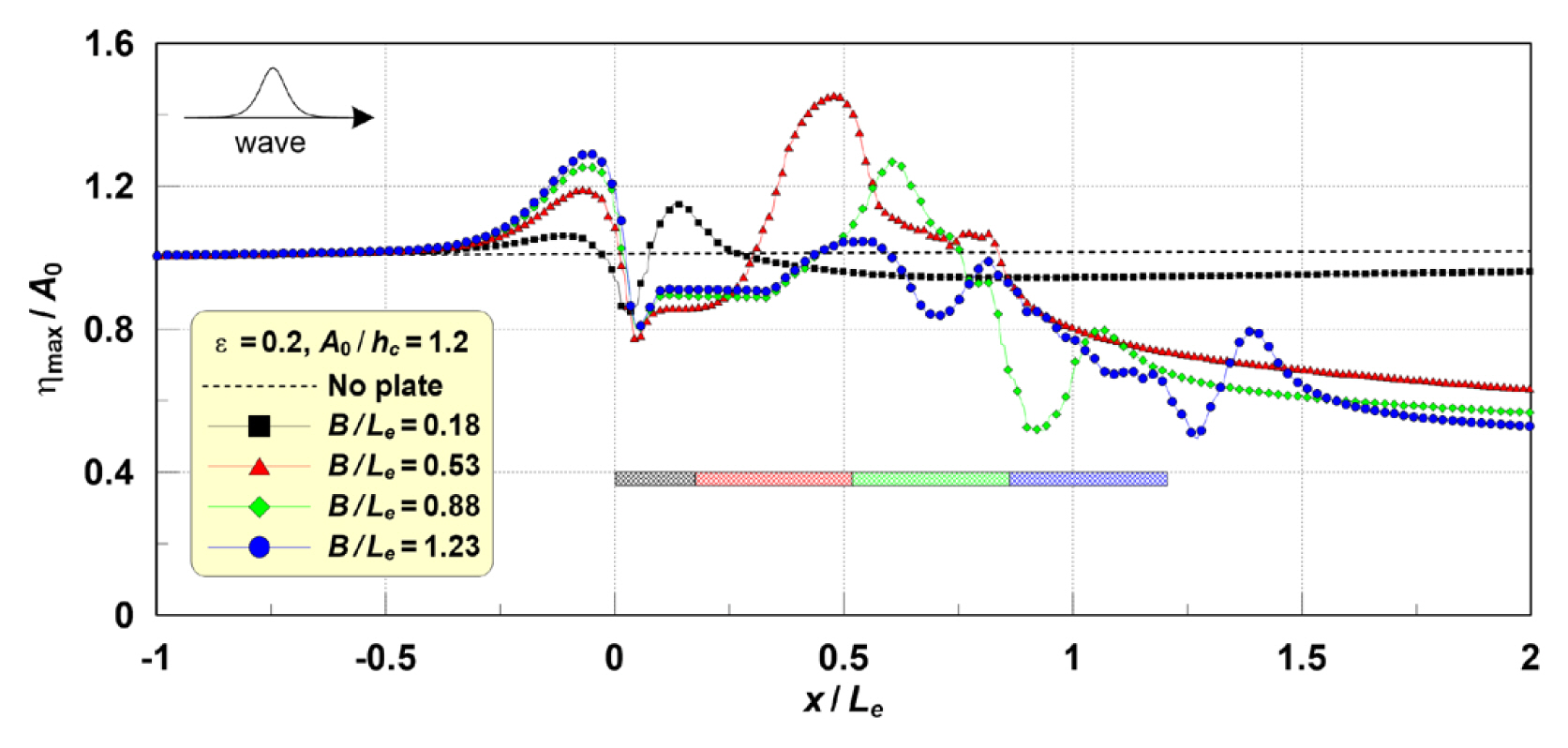
고립파와 SHP의 상호작용에 의한 에너지 소산이 파고 감쇠에 미치는 영향을 이해하기 위한 최대수위와 입사진폭의 비의 분포를 Fig. 10과 Fig. 11에 각각 나타낸다. Fig. 10은 B/Le=0.7 고정조건에서 A0/hc, Fig. 11은 A0/hc=1.2 고정조건에서 B/Le에 따른 고립파 감쇠현상을 비교한다.
Spatial distribution of maximum surface elevation according to A0/hc for ɛ = 0.2, B/Le = 0.7
Spatial distribution of maximum surface elevation according to B/Le for ɛ = 0.2, A0/hc = 1.2
앞에서 확인한 쇄파가 발생하는 경우, SHP 상에서 고립파의 최대수위가 급격히 하강할 뿐 아니라, 배후로 전달되는 진폭 또한 작아진다. 반면, 쇄파가 발생하지 않는 경우에는 SHP 상에서 상승한 최대수위가 서서히 하강하는 것을 볼 수 있다. 그리고 SHP 전면에서는 모든 계산조건에서 최대수위가 상승하는 경향을 보이고, A0/hc와 B/Le가 클수록 강하게 나타난다. 이 현상은 SHP에 의한 고립파의 반사에 큰 영향을 미칠 것으로 판단된다.
3.5 반사, 전달, 감쇠특성
Fig. 12는 SHP 설치 유무에 따른 전면(WG1)과 배후(WG5)의 시간파형을 각각 나타낸 것이다. SHP가 없는 경우에도 바닥마찰의 영향으로 WG5에서 파형변형이 발생함과 더불어 최대수위가 조금 감소하는 것을 확인할 수 있다. SHP가 설치됨에 따라 WG1에서는 입사파형과 반사파형이 시간차이를 두고 나타나고, WG5에서는 전달파형이 확인된다.
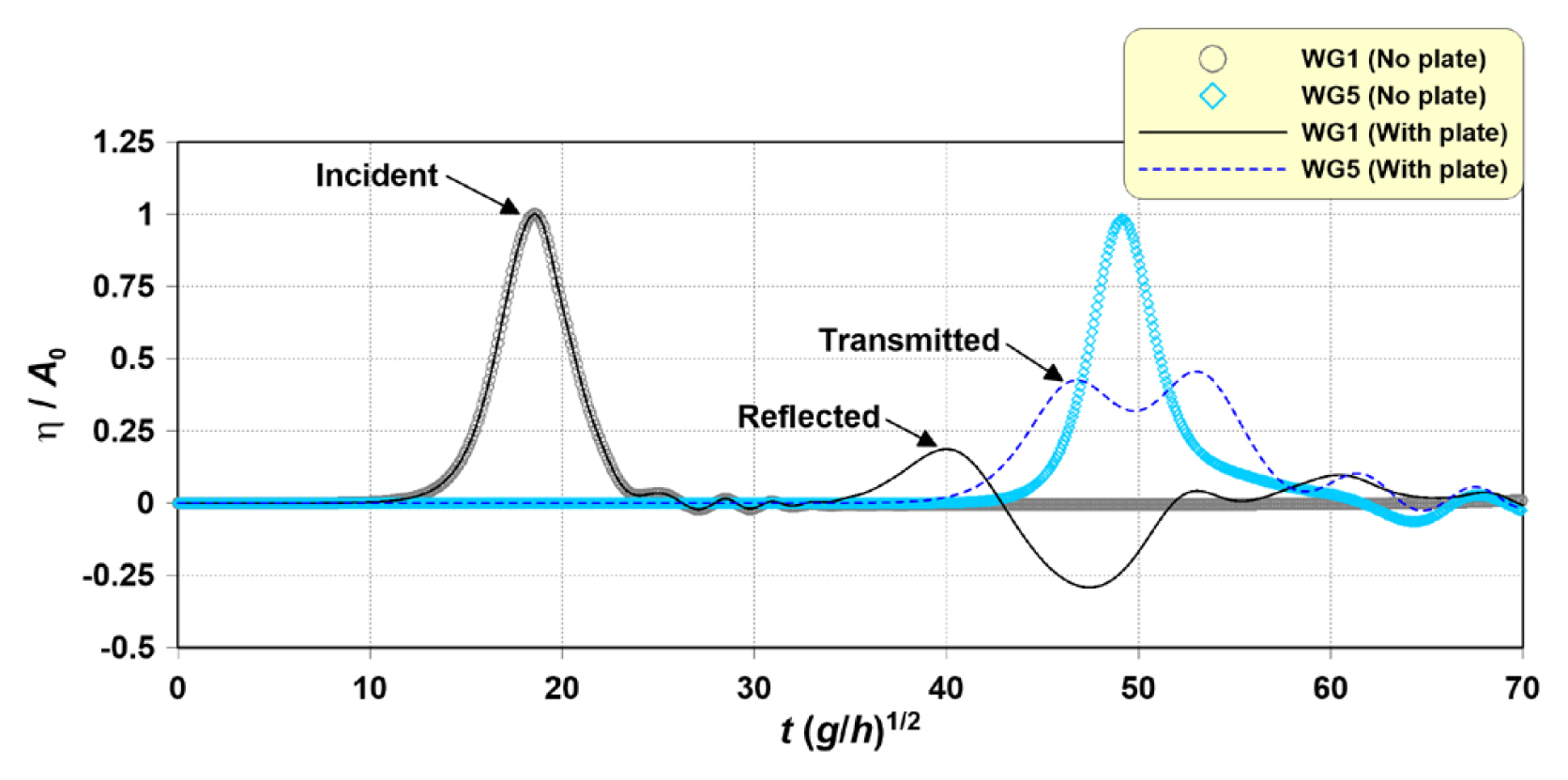
Time-domain waveform by a solitary wave propagation in the front (WG1) and rear (WG5) of SHP for ɛ = 0.3, A0/hc = 1.8, B/Le = 0.86
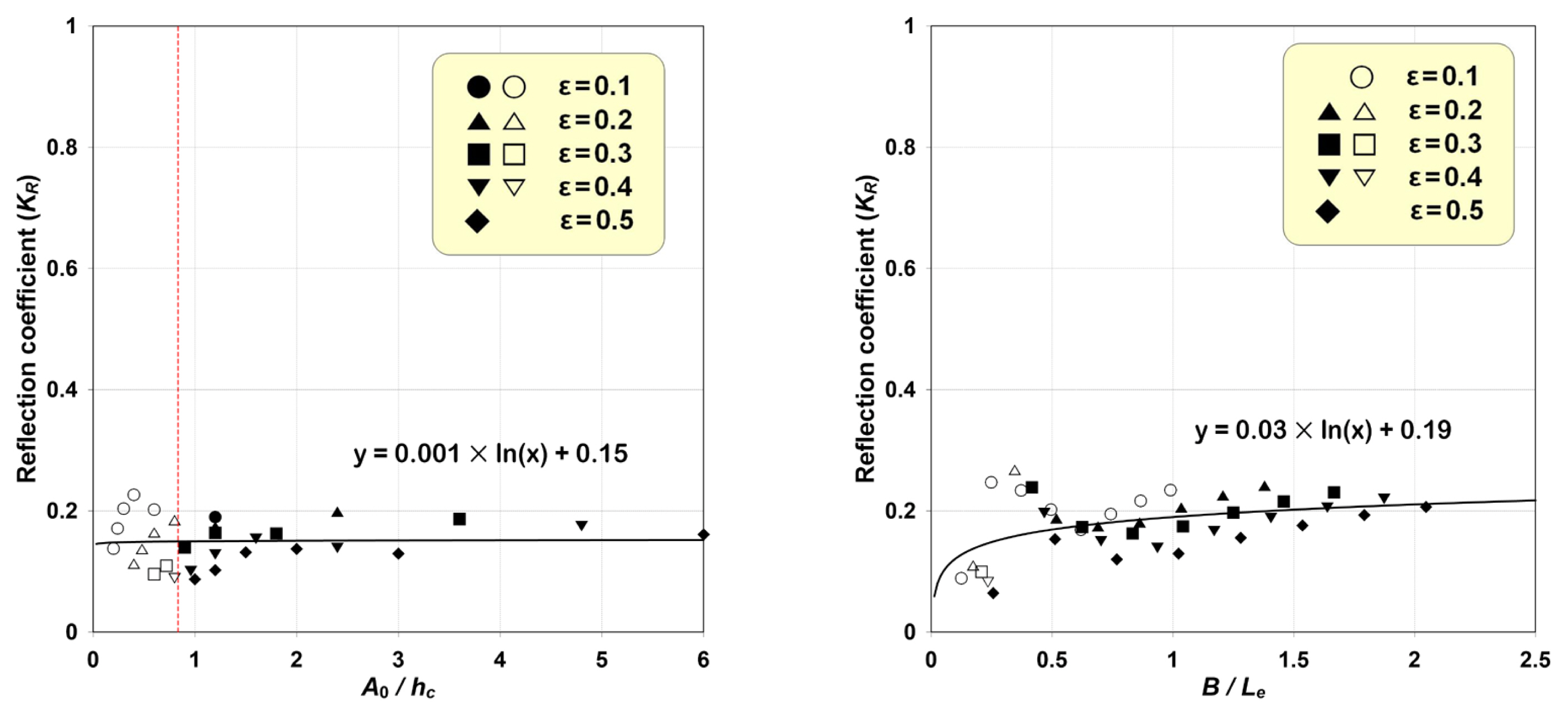
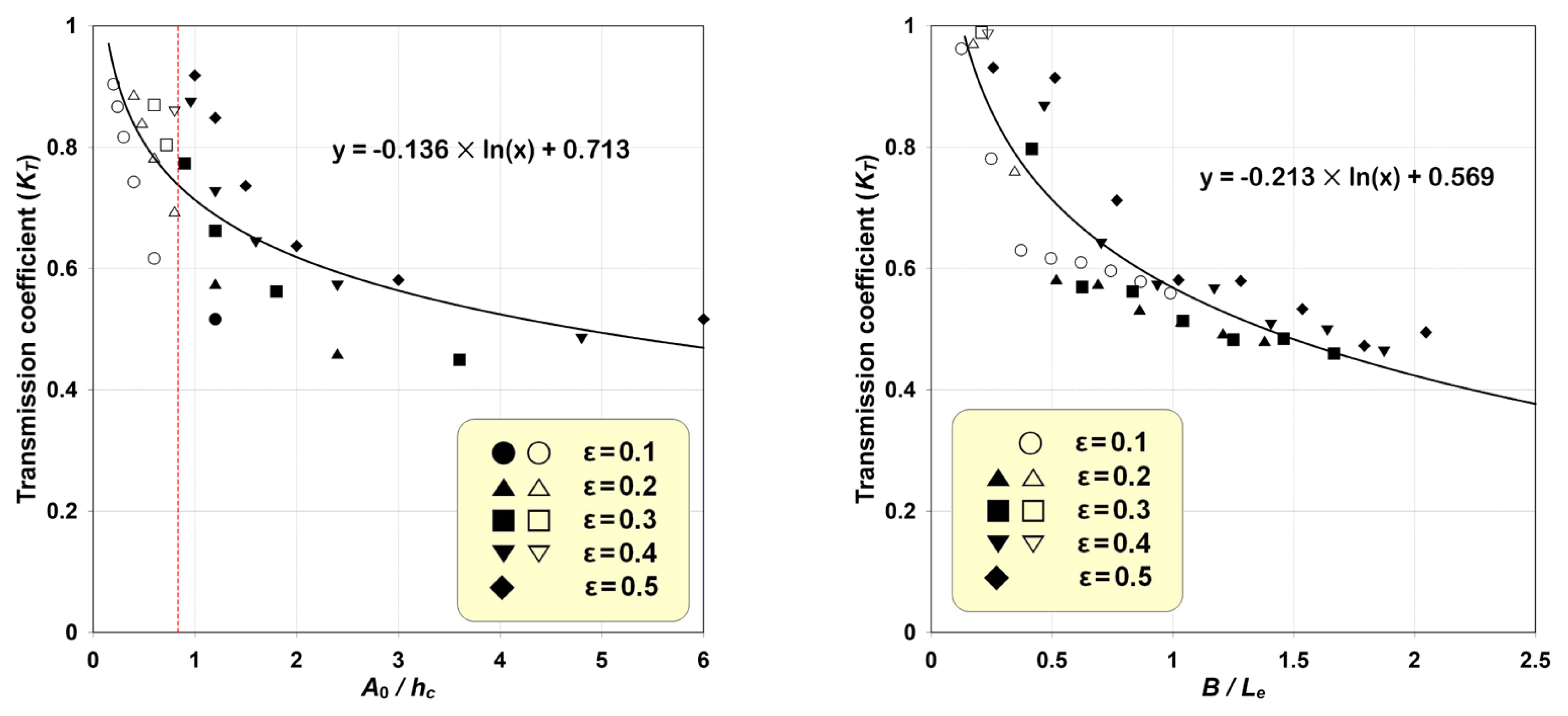
WG1과 WG5에서 확인할 수 있는 입사파, 반사파, 전달파를 분리한 후, 고립파의 반사계수(KR), 전달계수(KT), 에너지 감쇠계수(KD)를 각각 구하여 Figs. 13-15의 그래프에 나타낸다. Figs. 13-15에서 왼쪽 그래프는 B/Le=0.7 고정조건에서 A0/hc 변화, 오른쪽 그래프는 A0/hc=1.2 고정조건에서 B/Le 변화에 따른 계수들을 각각 나타낸다. 그리고 그래프에서 속이 찬 기호는 쇄파조건, 속이 빈 기호는 비쇄파조건에 해당한다. 붉은 수직 점선은 Witting(1975)과 Wu et al.(2005)의 고립파의 쇄파한계 A/h=0.833를 표시한 것이다.
Reflection coefficient according to A0/hc (left: B/Le = 0.69) and B/Le (right: A0/hc = 1.2)
Transmission coefficient according to A0/hc (left: B/Le = 0.7) and B/Le (right: A0/hc = 1.2)
Energy dissipation coefficient according to A0/hc (left: B/Le = 0.7) and B/Le (right: A0/hc = 1.2)
고립파-SHP 상호작용에 의한 고립파의 반사는 ε가 작을수록 조금 증가하는 경향을 보이나, 전반적으로 KR이 작아 큰 차이를 나타내지 못한다. 그리고 A0/hc에 따른 KR 분포는 뚜렷한 경향이 없으나, B/Le가 증가할수록 SHP의 유체저항이 증가함으로 KR의 완만한 상향 곡선이 나타나기도 한다. 한편, 고립파의 쇄파 유무에 따른 KR의 차이가 미소할 뿐 아니라, 이것으로부터 쇄파와 반사의 상관관계를 분석할 수 없다. 결과적으로 SHP 상에서 발생하는 고립파의 쇄파는 반사에 큰 영향을 미치지 않는 것으로 이해될 수 있다.
Fig. 14로부터 SHP 배후로 전달되는 고립파의 KT는 A0/hc와 B/Le가 커질수록 작아진다. A0/hc에 따른 KT 특성은 쇄파가 발생하지 않은 경우가 전반적으로 크고, 각 ε조건에서 일관된 경향을 나타낸다. ε조건별 A0/hc에 따른 KT 특성을 살펴보면, 비쇄파조건에서 커지고, 쇄파조건에서 작아지는 경향이 뚜렷이 구분된다. 이 결과는 SHP의 유체저항에 의한 고립파의 반사, 와류와 난류 생성에 따른 에너지소산, 쇄파로 의한 급격한 에너지 감쇠가 복합적 요인으로 작용하기 때문이다. 이 중에서 쇄파 유무가 고립파의 전달에 가장 큰 영향을 미치는 것으로 판단된다.
와류 및 난류 생성과 쇄파에 의한 에너지 감쇠를 정량적으로 나타낸 Fig. 15의 KD 특성을 살펴보면, A0/hc와 B/Le가 증가할수록 상향 분포를 나타낸다. KT 분포처럼 ε조건별 A0/hc와 B/Le에 따른 증가하는 유사한 경향을 나타낸다. 그리고 고립파의 쇄파 유무에 따라 KD 변화는 크게 구분된다. 한편, Fig. 15의 왼쪽 그래프에서 ε=0.1 조건에서는 쇄파가 발생하지 않는다. 이것은 B/Le>0.5 조건에서 SHP 경계 부근의 와류 및 난류의 발생시간과 거리가 늘어나 에너지 소산이 크게 나타나기 때문이다.
4. 결론 및 고찰
본 연구에서는 SHP의 고립파 제어 메커니즘을 분석하기 위한 수치해석을 수행하였다. 수치해석에는 2차원 NWT(Lee et al., 2016a)을 이용하였고, 고립파를 안정적으로 생성하기 위해 Lee et al.(2016c)의 조파방법을 도입하였다. 이용한 NWT의 타당성 및 유효성을 검증하기 위하여 Lo and Liu(2014)가 SHP 주변에서 측정한 파형과 계산파형을 비교하였다. 또한, 안정적으로 고립파가 생성되는지 확인할 목적으로 Dean and Dalrymple(1984)의 근사파형과 계산파형을 비교하였다. 비교⋅검증결과, SHP에 의한 고립파의 변형을 계산결과가 높은 정확도로 재현하였고, NWT의 입사파형 역시 근사파형과 거의 일치하였다. 고립파-SHP 상호작용에 관한 주요 수치해석결과는 다음과 같다.
1) 고립파의 전파과정에서 SHP 상⋅하의 유속 위상차로 인한 와도가 파봉 아래의 SHP 경계 부근에 강하게 발생하였다. 또한, SHP 상에서 발생한 쇄파로 인해 수면 부근에서도 강한 와도가 나타났다.
2) 고립파의 파봉 아래의 SHP 경계 부근의 난류에너지가 증가하였고, 쇄파시에는 수면 부근의 난류에너지가 매우 강하게 형성되었다.
3) SHP 상의 고립파 쇄파는 기존 한계조건 A0/hc>0.827-0.833에 부합하였으나, SHP의 폭이 좁은 경우에는 A0/hc=1.2 조건에서도 쇄파가 발생하지 않았다.
4) SHP 상의 고립파 쇄파로 인한 급격한 파고감쇠가 나타났다. 반면, 쇄파가 발생하지 않는 경우, SHP 경계 부근에 형성되는 와도 및 난류의 영향으로 고립파 에너지가 서서히 감소함으로 점진적 파고감쇠가 확인되었다.
5) 쇄파 유무 및 A0/hc 변화는 SHP에 의한 고립파 반사에 큰 영향을 미치지 못하였다. 그리고 B/Le에 따른 KR도 큰 차이를 나타내지 않았다.
A0/hc와 B/Le가 증가할수록 KT는 커지고, KD는 작아지는 경향을 나타내었다. 그리고 같은 ε조건에서 쇄파 유무에 따라 KT와 KD의 증가/감소폭이 뚜렷이 구분되었다. 향후, 수치모델의 신뢰성을 높이기 위한 추가검증을 수행할 뿐 아니라, 실제처럼 넓은 파형의 지진해일(Lee et al., 2017; Lee et al., 2018)에 대한 SHP의 파랑제어 효과를 검토할 예정이다.
Acknowledgements
이 성과는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2018R1C1B6007461).