1. 서 론
먼바다에서 여러 가지 기작에 의해 생성된 파랑은 인근 연안으로 전파되며, 이 과정에서 해양환경에 내재한 변동성으로 파랑은 불규칙한 모습을 지닌다. 이렇게 불규칙한 파랑 무리가 천해역에 진입하면 천수, 굴절, 회절 등으로 파랑 무리는 변화를 겪으며, 천수 최종단계에서 쇄파되며 긴 여정이 마무리된다 (Choi and Cho, 2019). 항 외곽시설은 이처럼 불규칙하고 거친 해양환경에 거치되기 마련으로 거친 해양환경에서도 충분한 내구성을 담보할 수 있도록 설계되어야 하나, 기존 호안 구조물의 피복석은 대부분 Hudson 식(SPM, 1984)에 의존한 결정론적 설계기법에 따라 설계됐다. 이러한 선호도는 Hudson 식이 갖는 편의성에 기초하나, Hudson 식은 그 유도과정을 살펴보면 적용 범위에 상당한 제약이 따른다는 사실을 쉽게 확인할 수 있다. 이러한 한계는 Hudson 식이 규칙 파, 소규모 수리모형실험에서 얻은 관측자료로부터 제시되었으며, 내습하는 파랑의 주기 혹은 폭풍 지속시간이 간과되었으며, 월파와 구조물의 투수 특성이 누락 된 사실 등에서 확인할 수 있다.
이러한 결정론적 해석의 한계를 해결할 수 있는 대안은 신뢰성 설계로 보이며, 신뢰성 설계는 방파제 내구성과 파력에 내재한 불확실성을 통계적으로 기술함으로써 안전도를 체계적으로 산정할 수 있다. 또한, 적절한 파괴확률을 수용함으로써 결정론적 설계기법에서 불필요하게 보수적으로 운영될 수 있는 부분들을 특정할 수 있어 상당한 비용 절감 효과를 얻을 수 있다. 파랑에 내재한 불규칙성을 고려하는 경우 전술한 신뢰성 설계는 장기 파랑 관측자료에 기초하여 진행되어야 하나, 우리나라의 경우 현재 장기간에 걸쳐 연속해서 관측된 파랑 자료가 가용하지 않는 경우가 대부분으로 이 경우 유럽 혹은 미국에서 선호되는 확률모형을 단순 수용하여 신뢰성 설계가 수행되는 것으로 보인다 (Kim et al., 2005; Kim et al., 2009; Suh et al., 2003). Van der Meer 식에 기초하는 경우 사석방파제 피복석 파괴 여부를 결정하는 확률변수는 파형 경사와 파고로 보이며, 파고의 경우 현재 가용한 확률모형으로는 단기 파랑 자료의 경우 먼바다를 대상으로 한 Rayleigh 분포, 천해역를 대상으로한 복합 Weibull 분포(Battjes and Groenendijk, 2000), 수정 Glukhovskiy 분포(Klopman and Stive, 1989) 등이, 장기 파랑 자료의 경우 삼 변량 Weibul 분포 등이 현재 문헌에서 가장 빈번하게 언급된다 (Forristall, 2008; Choi and Cho, 2019; Cho et al., 2019).
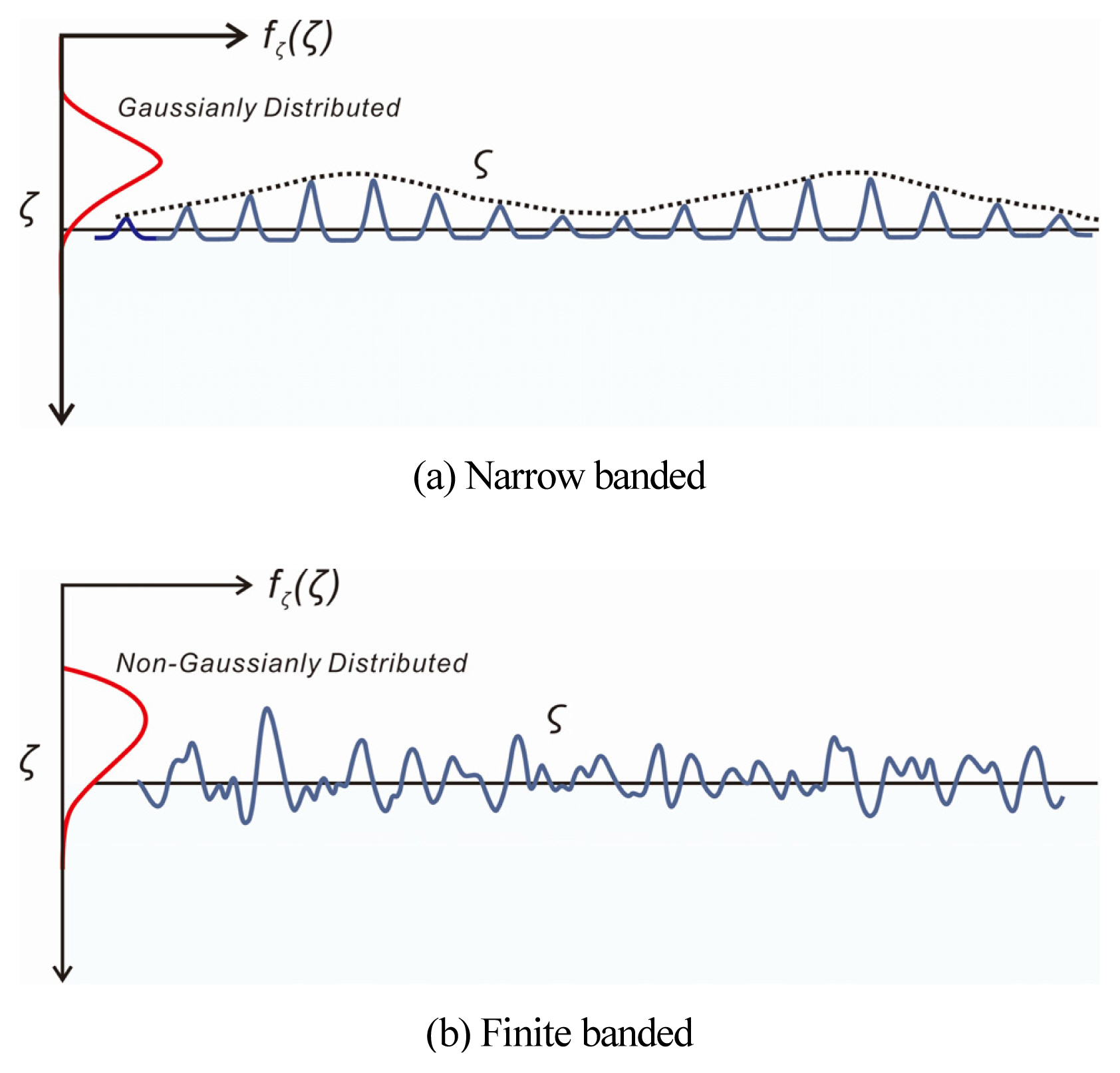
이렇듯 연구성과가 상당한 파고 분포와 달리 파형 경사분포는 소홀히 다루어져, 국내의 경우 먼저 파고를 전술한 확률모형에 기초한 Monte Carlo simulation으로부터 모의하고, 이어 간단한 경험식을 활용하여 모의 된 파고로부터 주기를 산출하고, 이렇게 산출된 파고와 주기로부터 파형 경사를 추정하는 경험적 방법이 주류를 이룬다. 이 과정에서 우리나라의 경우 주기는 파고에 선형 비례하는 것으로 간주되어 왔으나(Kim et al., 2005; Kim et al., 2009; Suh et al., 2003), Cavanie et al. (1976), Longuet-Higgins (1983), Park and Cho (2019), Cho (2021)의 연구성과에 따르면, 파고가 상대적으로 큰 경우 파고와 주기는 상관관계가 옅어져 상호 독립적인 무작위 과정으로 거동한다. 이러한 거동은 전술한 주기가 파고에 선형 비례한다는 회귀식에 기반한 경험적 방법은 상당한 오류가 초래될 수 있음을 의미한다. 이에 반해 유럽 혹은 미국의 경우 파형 경사는 Gaussian 분포를 따르는 것으로 추정되어왔으나 (PIANC, 1992), Gaussian 분포는 음의 파형 경사에도 작지 않은 발생확률을 부과하는 등의 한계를 지닌다. 또한, 최근 Cho and Kim(2019), Cho et al.(2019)의 연구성과에 따르면 유럽 혹은 미국의 파랑과 우리나라 동해안에서 관측되는 파랑 사이에는 상당한 구조적 차이가 존재하며, 이러한 구조적 차이는 미국의 경우 태평양에 직접 노출되어 상당한 방위에서 파랑 발달에 필요한 취송거리가 확보되나, 우리나라 특히 동해안의 경우 반시계 방향으로 틀어진 모양의 동해에 노출되어 파랑 발달에 필요한 충분한 취송거리가 제한적인 방위에서만 확보되는 지형 특성에 기인한다. Cho and Kim(2019), Cho et al. (2019)에 따르면 이러한 추론의 논거는 상대적으로 긴 전파과정에서 단주기의 파랑은 느린 파속으로 인해 파랑 무리로부터 분리되어 미국의 경우 장주기의 너울이 우월하나, 우리나라 특히 동해안에서는 다양한 주기의 너울이 관측된다는 사실 등에서 찾을 수 있다.
최근 Cho (2021)의 연구성과에 따르면 공진성 wave-wave interaction에 의해 파랑 무리에 외중력파가 출현하는 경우 파형 경사분포는 상당한 변화를 겪으며 파형 경사분포에는 확률 고원[probability plateau]이 생성된다. 이 연구에서는 Cho (2021)는 온화한 해양환경에서 내습하는 너울 무리에 혼재하는 외중력파가 황천시 일시적으로 침식된 해빈의 점진적 복원과정을 주도한다는 사실에 준거하여, 전술한 확률 고원[probability plateau]은 해안선 전진 혹은 후퇴와 밀접하게 연계된다는 가설을 세우고 우리나라 동해안 맹방해변에서 일 년에 걸쳐 수집된 해안선 관측자료를 토대로 전술한 상관관계를 특정한 바 있다. 이렇듯 파형 경사는 불규칙 파랑에 관한 가장 포괄적인 정보를 제공하나, 구주에서 선호하는 Gaussian 파형경사 분포는 단순 선형모형으로 천수 과정에서 상당한 변화를 겪는 파랑 무리의 비선형 역학 특성을 반영할 수 있는 어떠한 기제를 지니고 있지 않다. 이 밖의 파형경사 분포로는 Cox and Munk (1954a, 1954b, 1956)가 제시한 Gram Charlier distribution를 문헌에서 찾아볼 수 있으나 Gaussian 파형경사 분포 대비 개선되는 정도는 미미하며 파형 경사가 급하거나 해수면 변위가 큰 경우 음의 발생확률을 제시하는 등의 오류를 지닌다.
이러한 인식에 기초하여 본연구에서는 Non-Gaussian 파형 경사분포가 항외곽시설 피복석 안전에 미치는 영향을 수치 모의를 활용하여 살펴보려 한다. 수치 모의는 Van der Meer 식과 Monte Carlo simulation을 활용한 Level III 신뢰성 설계기법을 활용하여 수행되며, 이 과정에서 확률모형으로는 파고 분포의 경우 Choi and Cho(2019)가 JMA(Japan Meteorological Agency), NOAA(National Oceanic and Atmospheric Administration) 해상풍 자료와 SWAN에 기초하여 2003년 1월 1일부터 2017년 12월 31일까지 한 시간 간격으로 역 추산된 울산 전면해역에서의 유의 파고와 첨두 주기 시계열 자료로부터 유도한 수정 Glukhovskiy 계열 파고 분포, 울릉도 전면해역에서 1979.1.1.~2019.12.31. 사이에 수집된 파고 관측자료가 활용된다 (Jeong et al., 2018).
파형경사의 경우 최근 Cho (2021)가 Longuet-Higgins(1983)의 진폭⋅주기 결합 확률분포로부터 확률변수 변환기법(Papoulis, 1984)을 활용하여 해석적으로 유도한 파형 경사분포가 가장 수월성을 지니는 것으로 보인다. 이 연구에서 Cho(2021)는 전술한 파형 경사분포가 천수과정에서 공진성 wave-wave interaction으로 파동계에 외중력파가 출현하는 경우 주기가 긴 외중력파의 성정으로 인해 파형 경사분포에 형성되는 확률고원의 기술이 가능함을 situ wave data로 부터 예증하여 모형의 수월성을 확인된 바 있다.
전술한 Non-Gaussian 파형경사 분포를 신뢰성 설계에 적용하기 위해서는 황천 시 내습하는 파랑의 스펙트럼 bandwidth parameter에 대한 정량적 평가가 선행되어야 하나, 우리나라의 경우 아직 이루어지지 않아 적용이 어렵다. 이러한 어려움을 해결하기 위해 맹방 해빈 전면해역 수심이 26.5m인 지점[129° 13′ 34.56″ E 37° 24′ 11.22″ N]에서 초음파식 파고계[Nortek]를 활용하여 2017.4.26. ~2018.4.20 사이에 실측된 파랑 관측자료 (Cho and Kim, 2019; Cho et al., 2019)로부터 파형경사 분포를 산출하였다. 이 과정에서 외중력파 출현시 파형 경사분포에 생성되는 확률고원[probability plateau]를 확인하고 이 경우 여러 확률분포를 기저 분포로 활용한 검증 과정에서 가장 우월한 적합도를 보인 Tri-modal Gaissuian 분포를 활용하였으며 Tri-modal Gaussian분포의 확률모수는 Matlab 기반 Statistics and Machine Learning Toolbox 중 MLE [Maximum Likehood Estimates]를 활용하여 산출하였다.
2장에서는 이해를 돕기 위해 현재 가용한 Level I, II 피복석 신뢰성 설계를 정리하였으며, 3장에서는 현재 가용한 파고와 파형 경사 확률모형을 정리하였다. 3장에서는 우리나라 해양환경에 최적화된 파고 확률모형과 Non-Gaussian 분포 파형 경사분포를 같이 다루었다. 4장에서는 확률변수 변환기법을 활용하여 우리나라 해양환경에 최적화된 확률모형 유도과정과 Van der Meer 식에 기초한 호안 구조물 피복석 파괴확률 수치 모의 결과를 정리하였으며, 5장에서는 수치 결과를 다룬다.
2. 피복석 설계
2.1 결정론적 설계 - Van der Meer식
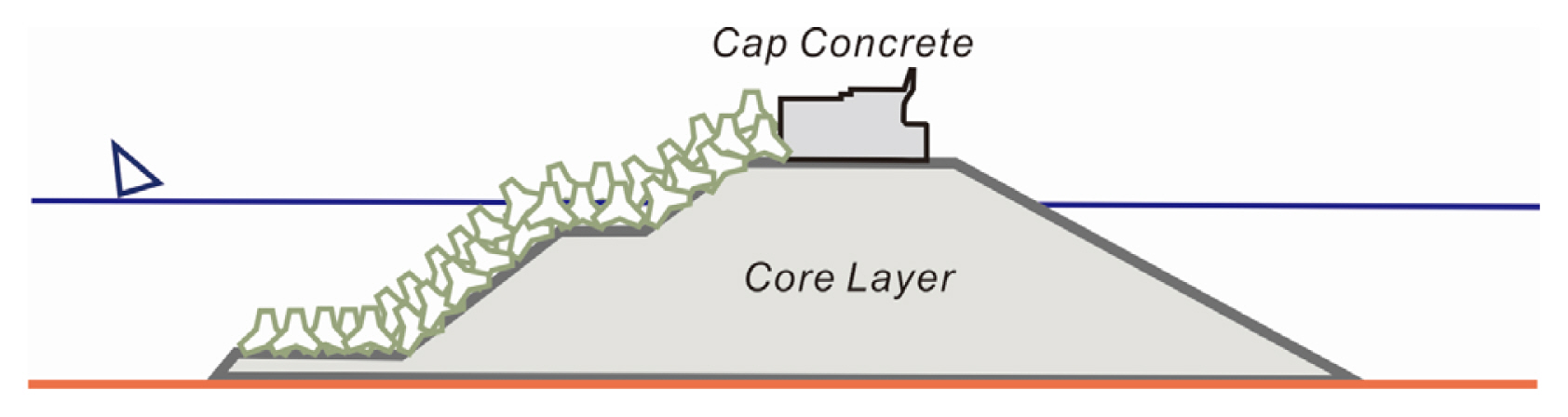
Van der Meer(PIANC, 1992)는 Thompson and Shuttler(1975)의 초기 작업을 토대로 일련의 수리모형 실험을 Delft Hydraulics에서 수행한 바 있다. 이 실험은 다양한 파랑 조건과 피복층/중심부 투수특성을 포함한 가장 광범위하게 수행되었으며 수행과정에서 축적된 자료를 토대로 Van der Meer는 권파와 쇄기파를 대상으로 경험식을 제안하였으며, Tetrapod로 구성된 사면 경사 1:1.5인 피복 층의 경우 Tetrapod의 크기는 다음과 같이 산출된다[Fig. 1 참조].
식(1)에서 △는 ρrock/ρwater -1로 정의되는 상대밀도, Dn50 = (WTTP/ρrock)1/3는 공칭지름[Nominal Diameter], WTTP는 피복석 무게, Nod는 평균 해수면 인근의 침식 면적을 공칭지름으로 나눈 침식 계수[Relative Damage Level], Som은 파형 경사, Nz는 내습하는 파랑 수, ρrock는 ρwater는 각각 피복석과 해수의 밀도를 나타낸다.
Van der Meer 식의 물리적 의미를 더욱 확연히 드러내기 위해 각 항을 세분하는 경우 다음과 같이 기술할 수 있으며
여기서 확률변수는 굵은 체로 표기하였다. 따라서 피복층 강도 R이 파력 S보다 작은 경우 사석방파제 피복층은 불안정하며 반대의 경우 안정적이라 할 수 있다.
2.2 신뢰성 설계
2.1절에서 다룬 결정론적 설계법은 신뢰성 설계법에서는 Level 0으로 분류되며, Van der Meer (1988)는 식(2)에 근거하여 파고의 피복석 공칭지름에 대한 비율이 구조물의 내 구성을 결정한다고 보았으며 이러한 시각은 다음에 기술되는 Level I 부분 안전계수 법으로 이어진다.
2.2.1 부분안전계수 법[Level I]
Van der Meer (PIANC, 1992)는 방파제 피복석 파괴여부를 결정하는 Nod, Nz, ∆, Dn50, Hs, Som 등과 같은 확률변수에 내재한 불규칙성을 각 확률변수에 대한 확률모형을 도입하여 설명하기보다는 해석의 편의를 위해 Nod, Nz, ∆, Dn50, Hs, Som라는 상호 독립적인 6개의 무작위 과정을 먼저 피복층 내구성과 파력으로 구분하고, 이어 내구성과 파력에 내재한 불규칙성을 총괄하는 강도 감소계수 γZ 와 하중 증가계수 γHs를 도입하여 설명하려고 시도하여 부분적인 성과를 거둔 것으로 보인다.
이 경우 방파제 신뢰성은 다음과 같이 기술될 수 있다.
식(3)에서 강도 감소계수 γZ 와 하중 증가계수 γHs는 각각 다음과 같이 정의되며 (Burcharth and Sorensen, 1999),
여기서 T는 설계내용 년 수, Pf는 내용기간 중 목표 파괴확률, FHs는 Hs의 단기 오차 변동성을 설명하기 위해 도입된 계수로 확률변수로 다루어지며, σFHs ′는 FHs의 정규화 분산계수(PIANC, 1992), HsT 는 내용 년 수 T의 조우 확률에 해당하는 유의 파고, Hs3T 는 내용 년 수 T의 3배에 해당하는 기간의 조우 확률에 해당하는 유의 파고, HsTPf는 재현 기간 TPf에 상응하는 유의 파고, TPf 는 목표 파괴확률 Pf에 해당하는 재현 기간, N는 극치 분포의 모수 추정에 사용된 자료의 수, kα, kβ, ks 는 각각의 파괴확률로부터 최적화된 계수를 나타낸다.
2.2.2 Level II
Level II 신뢰성 설계는 각 확률변수의 평균과 분산 그리고 분포형태만을 이용하여 파괴확률의 간접 지표인 신뢰도 지수를 근사적으로 산정하는 방법으로 모멘트 법이라고도 한다. 확률변수들의 확률분포를 직접 이용하지 않고도 각 변수의 불확실성을 고려할 수 있으며 근사 방법에 따라 FMA와 AFDA로 분류된다.
- FMA[First order Mean value Approach]
신뢰성 함수 Z(한계상태식)가 정규분포 확률변수의 비선형식으로 주어졌을 경우 각 확률변수의 기대평균치 주변에서 Taylor Series로 전개하여 선형 한계상태 식으로 근사시켜 1차 항만을 고려하는 방법이다. 확률변수의 상호독립과 정규분포를 가정하며, 확률변수의 선형 근사 식에서 신뢰성 지수 β를 구한다. 이때, β는 신뢰성 함수[Z]의 평균에서 한계상태[Z=0]까지의 상대적 거리를 의미한다.
- AFDA[Approximate Full Distribution Approach]
정규분포를 따르지 않는 변수들 사이의 상관관계를 고려하여 신뢰성을 해석하는 방법이다. 그러나 이 방법에서도 각각의 확률변수들 사이의 상관관계가 가정되든지 아니면 관련 자료로부터 미리 구하여 입력 자료로 주어져야만 한다. 즉, 상관계수와 관련된 고유치와 고유벡터를 구하여 그에 따른 영향들을 해석하는 방법으로(Ang and Tang, 1990), FMA와 유사하나 신뢰성 함수의 선형화를 기대평균치가 아닌 MPFP(Most Probable Failure Point or Design Point)의 주변을 중심으로 전개하는 차이가 있다.
3. 확률모형
3.1 파고 분포
Rayleigh 파고 분포함수 FH(h)는 현재 해안공학 계에 가장 널리 알려진 확률모형으로, 선형모형임에도 불구하고 심해 불규칙 파랑의 경우 일치도가 상당하나(Longuet-Higgins, 1952), 항 외곽시설이 거치되는 유한 수심의 경우 천수, 굴절 등과 같은 변형으로 인해 파랑의 비선형성은 무시할 수 없을 정도로 증가하며 파고 분포는 상당한 변화를 겪는다. 이러한 유한 수심에서의 파고 분포는 Glukhovskiy(1966)에 의해 처음 제시된 이래, 초기 모형이 지니는 모수 산정 과정의 불확정성(Battjes, 1986)이 Klopman and Stive(1989), Klopman (1996) 등에 의해 개선되는 등 꾸준히 진화되어 현재 수정 Glukhovskiy 분포는 대표적인 천해 역 파고 분포로 선호도가 상당하다(Choi and Cho, 2019).
그러나 수정 Glukhovskiy 분포는 천수의 마지막 단계인 쇄파역에서는 상당히 보수적인 값을 주는 것으로 알려졌으며(van Vledder et al., 2013), Battjes and Groenendijk(2000)는 이러한 단점을 개선하기 위해 파고 표본공간을 두 개로 분리하여 쇄파에 따른 파고 감쇄를 설명한 복합 Weibull 파고 분포를 제시하였다. 이후 Battjes and Groenendijk의 복합 Weibull 분포는 대표적인 쇄파역 파고 분포로 선호된다(Choi and Cho, 2019). 이 밖에 장기 유의 파고 확률분포함수로 문헌에서 가장 선호되는 모형으로는 삼 변량 Weibull 분포함수 등이 있다.
이해를 돕기 위해 3.1.1, 3.1.2, 3.1.3절에는 Rayleigh 파고 분포, Glukhovskiy 파고 분포, 복합 Weibull 파고 분포를 정리하였으며, 3.1.4, 3.1.5절에는 삼 변량 Weibull 분포함수, 우리나라 해양환경에 최적화된 파고 확률 모형을 각각 정리하였다.
3.1.1 Rayleigh 분포
Rayleigh 파고 분포 FH (h)를 유의 파고 HS를 중심으로 기술하면 다음과 같으며(Longuet-Higgins, 1952),
여기서 P[H <h]는 불규칙 파고 H가 h보다 작은 확률을 나타낸다.
3.1.2 수정 Glukhovskiy 분포
수정 Glukhovskiy 파고 분포함수 FH (h)를 기술하면 다음과 같으며,
여기서 A와 κ는 수정 Glukhovskiy 파고 분포함수의 모수로 d ~
식(7)에 정의된 수정 Glukhovskiy 파고 분포함수는 먼바다[d→∞]에서는 Rayleigh 분포로 수렴되는 것을 알 수 있다.
3.1.3 복합 Weibull 분포
정규화된 파고 h ~ F H ~ ( h ~ )
파고분포함수의 미분으로 정의되는 확률밀도함수 F H ~ ( h ~ )
여기서 H ~ 1 H ~ 2 H ~ t r
식(12)에서 d는 수심, α는 해저면 경사를 각각 나타낸다. 식(10)에서 알 수 있듯 복합 Weibull 분포함수의 구체적 형태를 결정하는 것은 k1, k2, H ~ 1 H ~ 2 H ~ t r
3.1.4 삼 변량 Weibull 분포
장기 유의 파고 확률분포함수로 문헌에서 가장 선호되는 모형은 삼 변량 Weibull 분포함수 FH (h)로 이를 기술하면 다음과 같으며(Forristall, 2008),
여기서 μh, HL, κL는 삼 변량 Weibull 분포함수의 모수로 회귀분석에 의해 결정된다.
3.1.5 우리나라 해양환경을 반영한 파고 확률모형
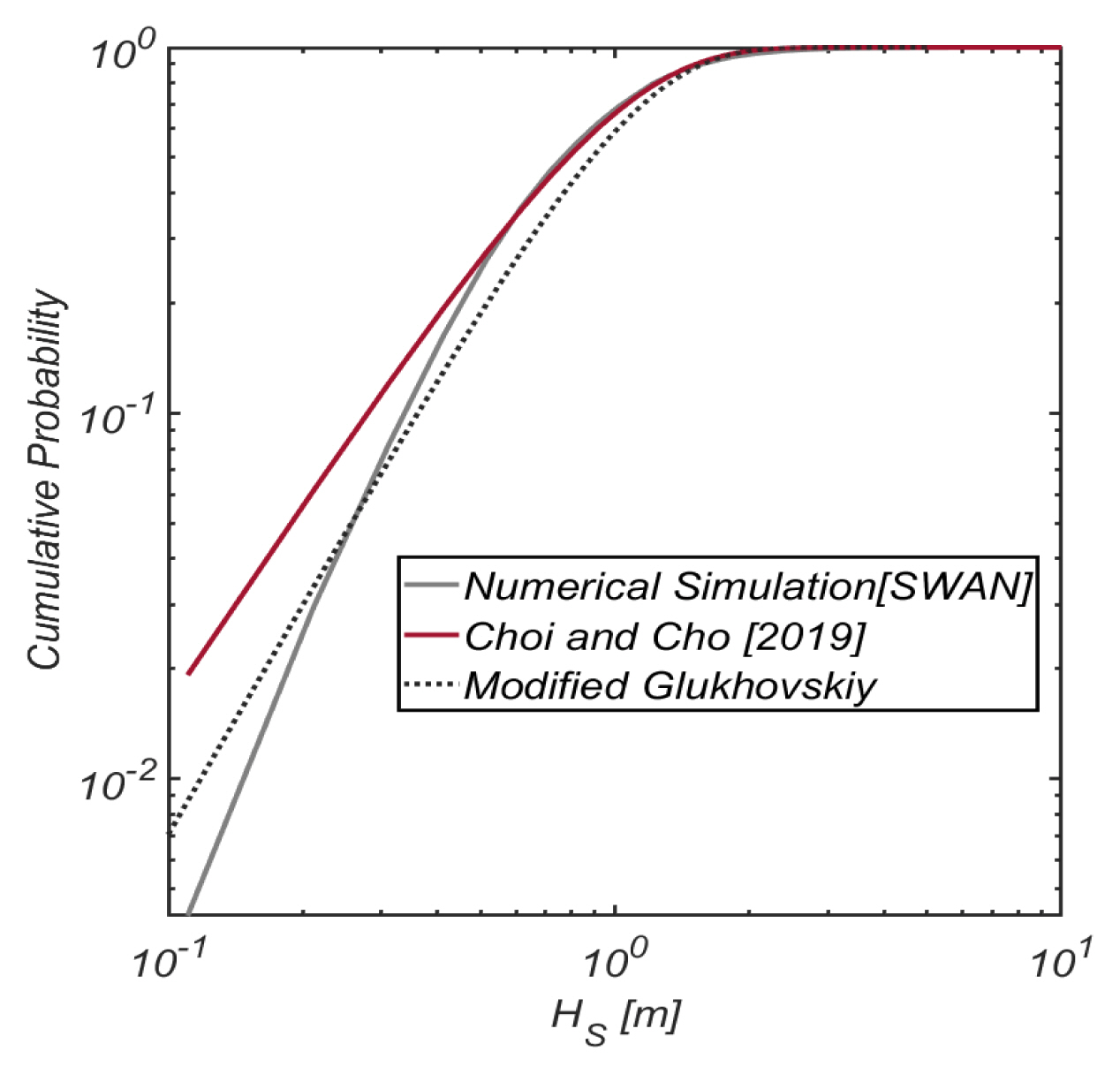
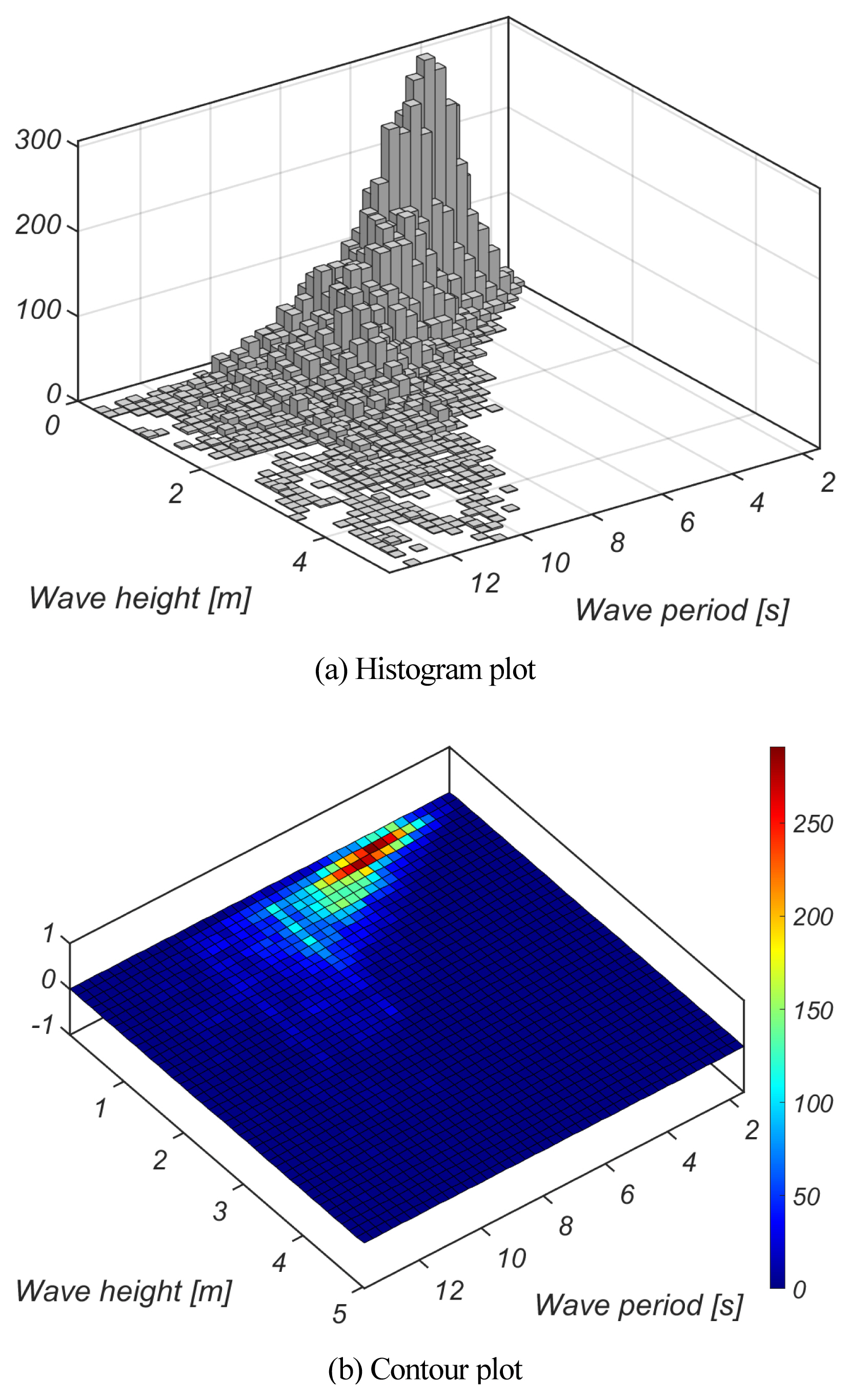
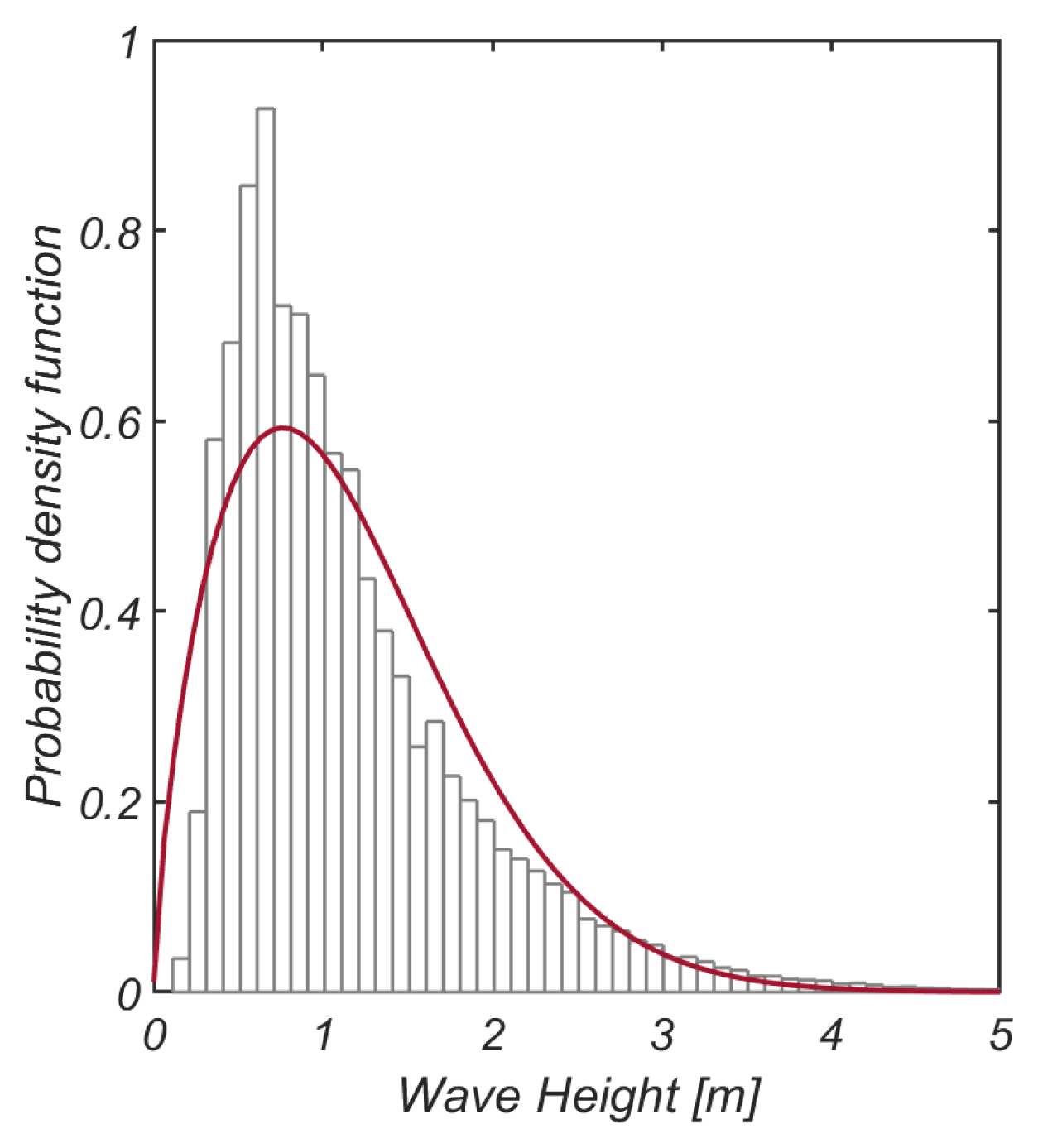
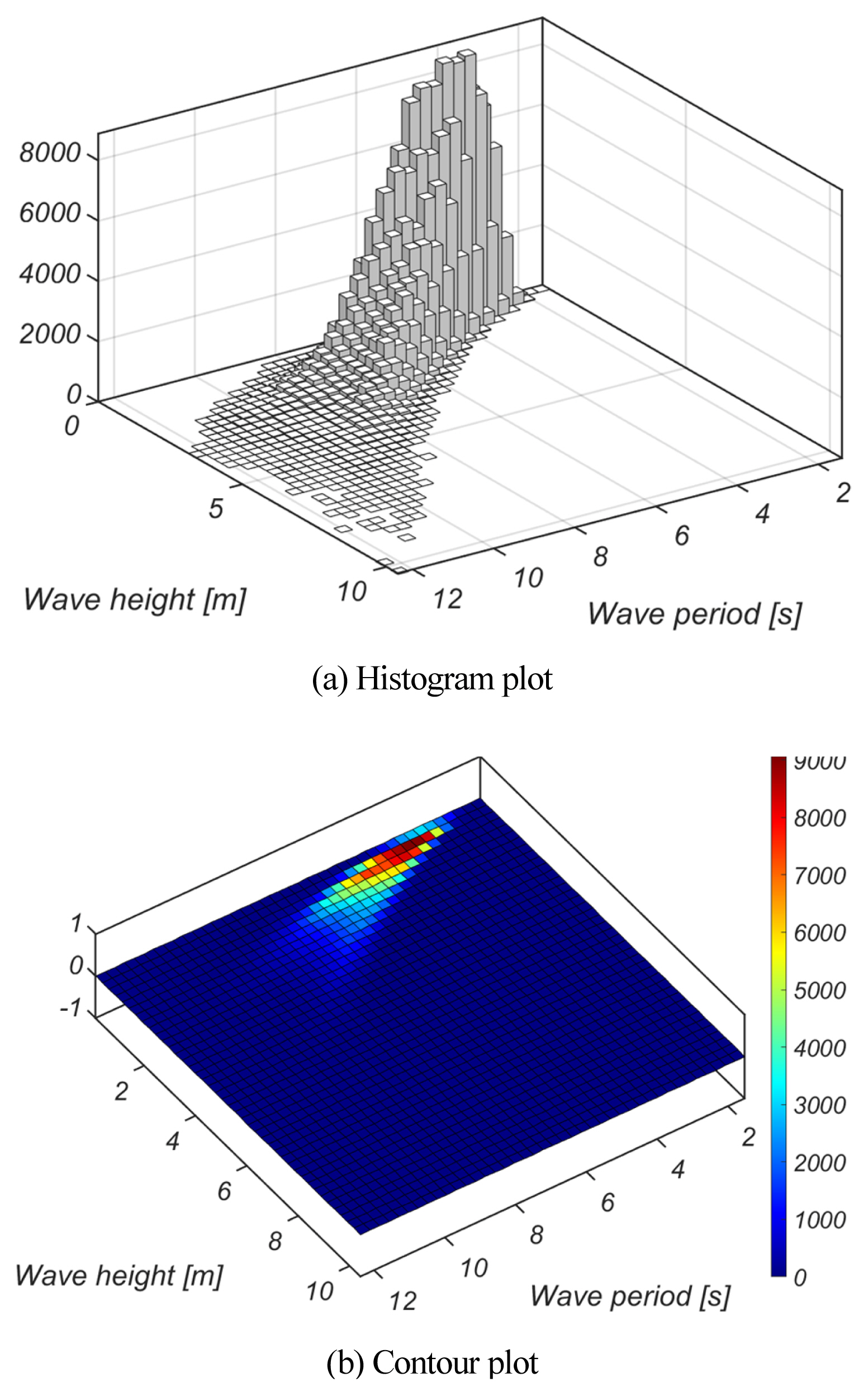
최근 Choi and Cho(2019)는 JMA[Japan Meteorological Agency]와 NOAA[National Oceanic and Atmospheric Administration]의 해상풍 자료와 SWAN에 기초하여 2003년 1월 1일부터 2017년 12월 31일까지 한 시간 간격으로 역 추산된 울산 전면해역에서의 유의파고와 첨두 주기를 활용하여 우리나라 해양환경에 최적화된 확률모형을 유도한 바 있다. 이 연구에서 Choi and Cho(2019)는 전술한 유의 파고 시계열 자료로부터 Matlab 기반 Statistics and Machine Learning Toolbox 중 MLE[Maximum Likehood Estimates]를 활용하여 산출하였다. 모의 결과 그동안 선호되던 삼 변량 Weibull 분포보다는 수정 Glukhovskiy 분포 계열에서 일치도가 가장 우월한 것으로 드러났다[Fig. 2, 3 참조].
Choi and Cho(2019)에 의해 유도된 수정 Glukhovskiy 분포계열 파고 확률밀도함수 fH(h)는 다음과 같이 정의되며,
이를 분포함수로 기술하는 경우 다음과 같다.
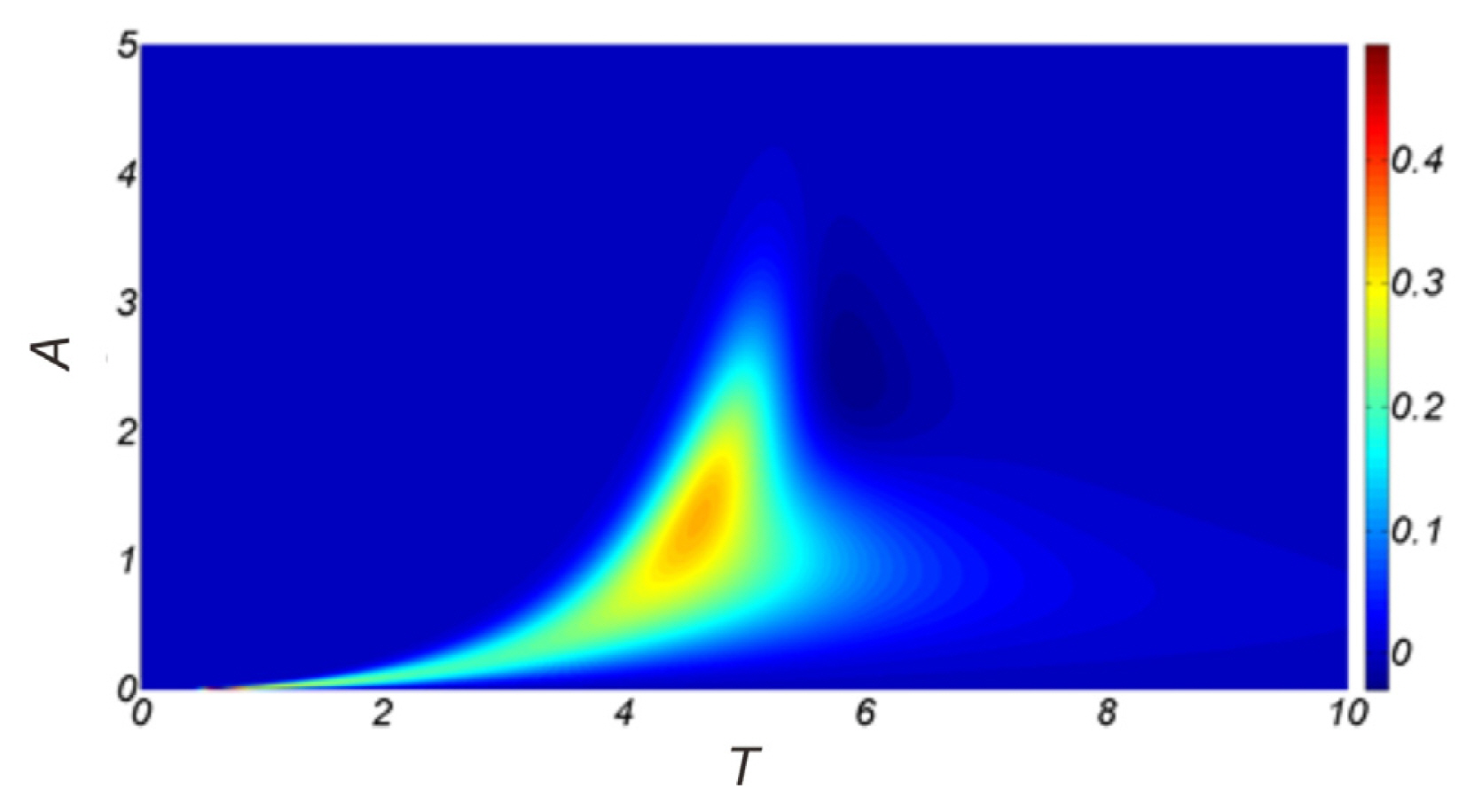
Choi and Cho(2019)에 의하면 식(15)에 정의된 수정 Glukhovskiy 분포의 모수 Ap, Hp, κp는 신뢰수준 95%에서 각각 Ap = 15.92, Hp = 4.374 m, κp = 1.824의 값을 지닌다. Fig. 4에는 울산 전면해역에서의 파황 특성을 드러내기 위해 파고와 주기의 결합확률분포를 정리하였다.
3.2 파형 경사분포
3.2.1 Gaussian 분포
사석방파제 피복층 강도를 결정하는 무작위 과정인 파형경사의 경우 유럽 혹은 미국에서는 Gaussian 분포를 선호하며(PIANC, 1992), 이를 기술하면 다음과 같다(CUR, 1998).
3.2.2 Non-Gaussian 파형 경사분포
본 절에서는 이해를 돕기 위해 전술한 Gaussian 분포의 대안을 제시하기 위해, Cho (2021)가 문헌에서 가장 빈번하게 언급되는 진폭과 주기의 결합 확률분포인 Longuet-Higgins(1983) 모형과 확률변수 변환기법(Papoulis, 1984)을 활용하여 해석적으로 유도한 파형 경사 확률분포 유도과정을 소개하고, 전술한 Gaussian 분포 대비 개선 정도를 살펴보고자 한다.
Non-Gaussian 분포 파형 경사 확률모형 유도과정을 정리하면 다음과 같다:
Longuet-Higgins(1983)이 제시한 진폭 A과 주기 T 결합 확률분포를 기술하면 다음과 같으며,
여기서 v는 bandwidth parameter를 나타내며 다음과 같이 정의된다(Longuet-Higgins, 1983).
식(18)에서 mi는 파랑 스펙트럼 Sζζ(ω)의 i차 모멘트를 나타내며 이를 기술하면 다음과 같으며,
여기서 ω는 angular frequency를 나타낸다.
무작위 파형 경사 Som 는 심해라는 가정을 수행하는 경우 다음과 같이 기술될 수 있으며,
여기서 Lo는 먼바다에서의 파장을 나타낸다.
Mapping에 필요한 관계식이 부족한 ill-posed 문제를 해결하기 위해 먼저 다음과 같이 정의되는 보조 확률변수를 도입하는 경우,
Som 와 SD 의 결합확률분포 fSomSD (Som, SD)는 확률변수 변환기법 (Papoulis, 1984)을 활용하는 경우 식(17)에 정의된 fAT(A, T) 로부터 해석적으로 유도할 수 있으며 이 과정을 기술하면 다음과 같다.
식(22)에서 Jacobian J는 [A, T] → [Som, SD] mapping에 해당하는 면적비를 나타낸다.
최종적으로 파형 경사 확률분포는 ill-posed 문제를 해결하기 위해 도입한 보조 확률변수 SD가 지닐 수 있는 모든 값을 대상으로 적분을 수행하여 얻게 되며[marginal integration], 이렇게 얻은 fSom (Som)를 기술하면 다음과 같다.
식(23)에서 f(SD)는 다음과 같이 정의된다.
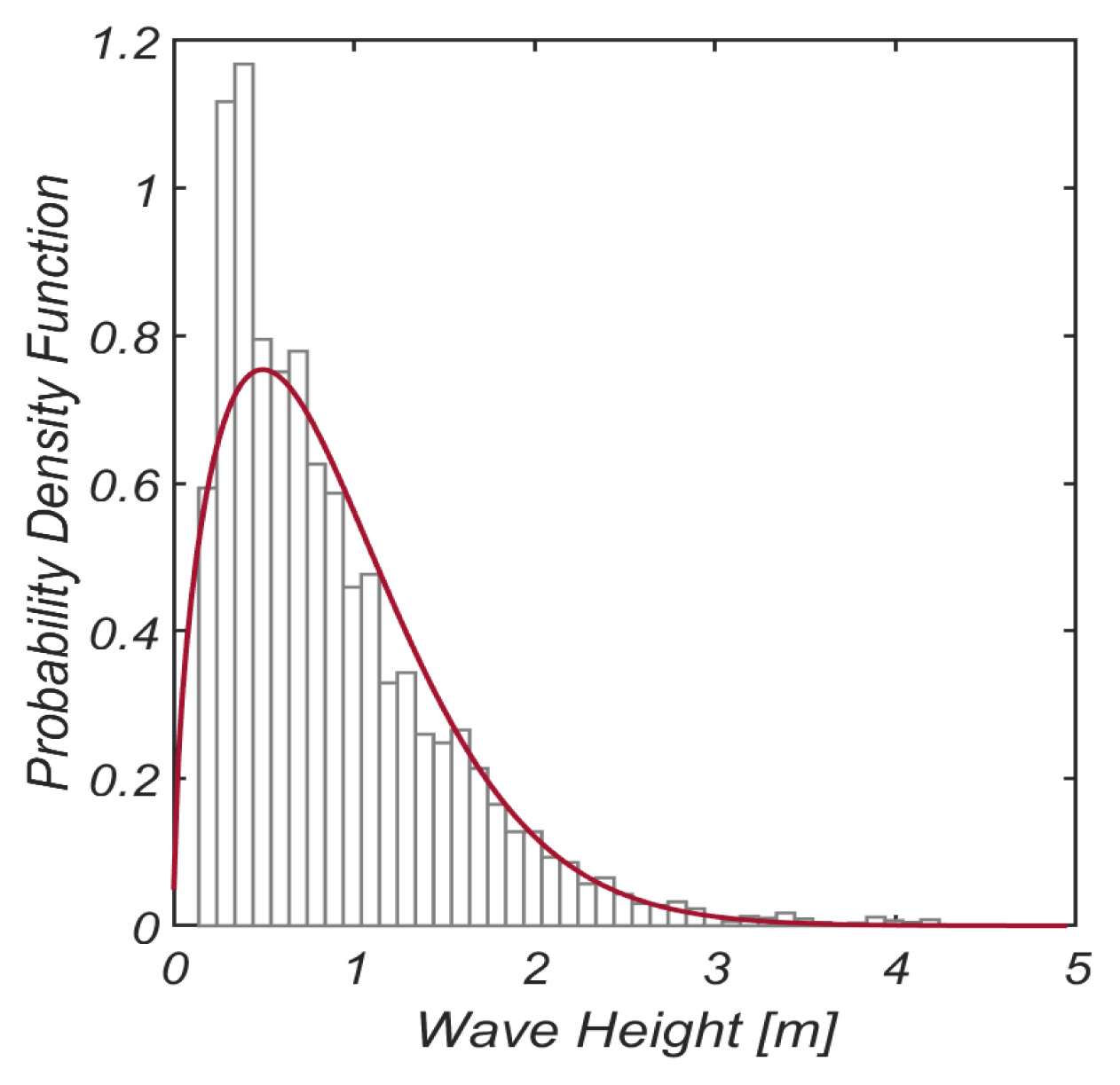
Fig. 5에는 v = 0.2, 0.3, 0.4에 대해서 수치 모의 된 fSom (Som)을 도시하였으며, Fig. 6에는 비교를 위해 본 논문에서 제시된 Non-Gaussian 파형 경사 확률분포와 같은 표준편차와 평균을 지니는 Gaussian 분포도 함께 도시하였다. Fig. 5에서 파랑 스펙트럼 bandwidth v의 증가는 거친 해양 환경과 이로 인해 파동계에 출현하는 성분 파랑 수가 증가하는 것을 의미한다. 이 경우 성분 파랑 간의 공진성 상호작용으로 파랑 에너지는 상대적으로 짧고, 긴 주기 대역으로 이동하며 이러한 경향은 Fig. 5에서 확연하게 찾아볼 수 있다[Fig. 7, 8 참조].
전술한 성분 파랑 간의 공진성 상호작용으로 해양환경이 거칠수록[v→1.0], 적지 않은 확률 질량이 상대적으로 급하고, 완만한 파형 경사 대역으로 이동하는 것을 Fig. 5, 6에서 확인할 수 있다. 이에 반해 Gaussian 분포의 경우 평균 파형 경사 인근과 극치 파형 경사에서 overshooting 하며, 음의 파형 경사에도 작지 않은 발생확률을 부과하는 등의 오류를 찾아볼 수 있다.
Non-Gaussian 파형 경사 확률분포에서 파형 경사가 작은 경우 발생확률이 영에서 급격히 증가하다 다시 완만해지는 거동이 흥미로우며 이러한 추이는 v가 증가할수록 더욱 확연해진다[Fig. 5, 6 참조]. 전술한 확률분포 변화추이는 풍성파 성장 과정을 다룬 Hasselmann(1967), Phillips(1977) 연구성과 이후 해안공학 계에서 널리 알려진 비선형 sub-harmonic 공진성 상호작용으로 파동계에 출현하는 장주기 파랑에 기인하는 것으로 판단된다. v 증가는 비선형성 증가를 함의하며 이 경우 공진성 상호작용으로 장주기 파랑의 발생확률이 현저하게 증가한다. 이렇게 장주기 파랑이 출현하는 경우 긴 주기로 인해 상대적으로 작은 파형 경사 발생확률은 증가한다. Fig. 4, 5에서 확인되는 확률분포 거동 추이는 비선형 불규칙 파동계의 sub-harmonic 공진성 상호작용에 기인하며 전술한 확률분포 거동 추이는 Fig. 7에 도시된 진폭 A와 주기 T의 결합 확률분포에서도 예단할 수 있다.
Van der Meer 식에 비추어보면 공진성 상호작용으로 인한 파형 경사 분포 변화는 피복석 강도와 파괴확률에 상당한 영향을 미치는 것으로 보이며, 따라서 전술한 기작을 설명할 수 있는 Non-Gaussian 파형 경사 확률분포[식(23) 참조]는 합리적 피복석 신뢰성 설계 구현에 상당한 역할을 할 것으로 기대된다.
3.2.3 Tri-modal Gaussian 파형 경사분포
3.2.2절에서 다룬 Non-Gaussian wave slope 분포는 현재 가용한 확률모형 중 가장 우월성을 지닌다. 전수한 Non-Gaussian 파형 경사 분포를 활용하기 위해서는 황천 시 내습하는 파랑의 스펙트럼 bandwidth parameter에 대한 정량적 평가가 선행되어야 하나, 우리나라의 경우 아직 이루어지지 않아 적용이 어렵다.
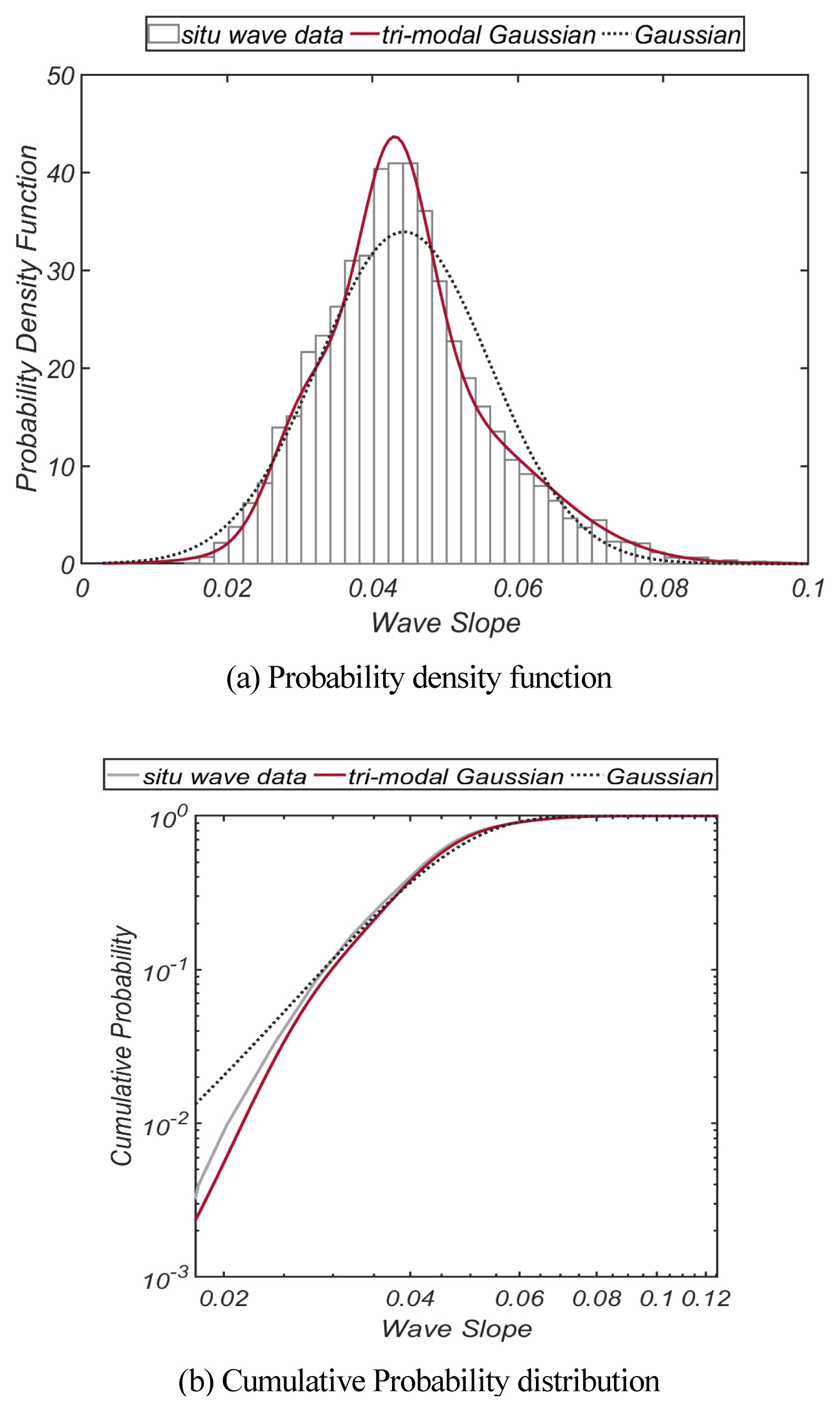
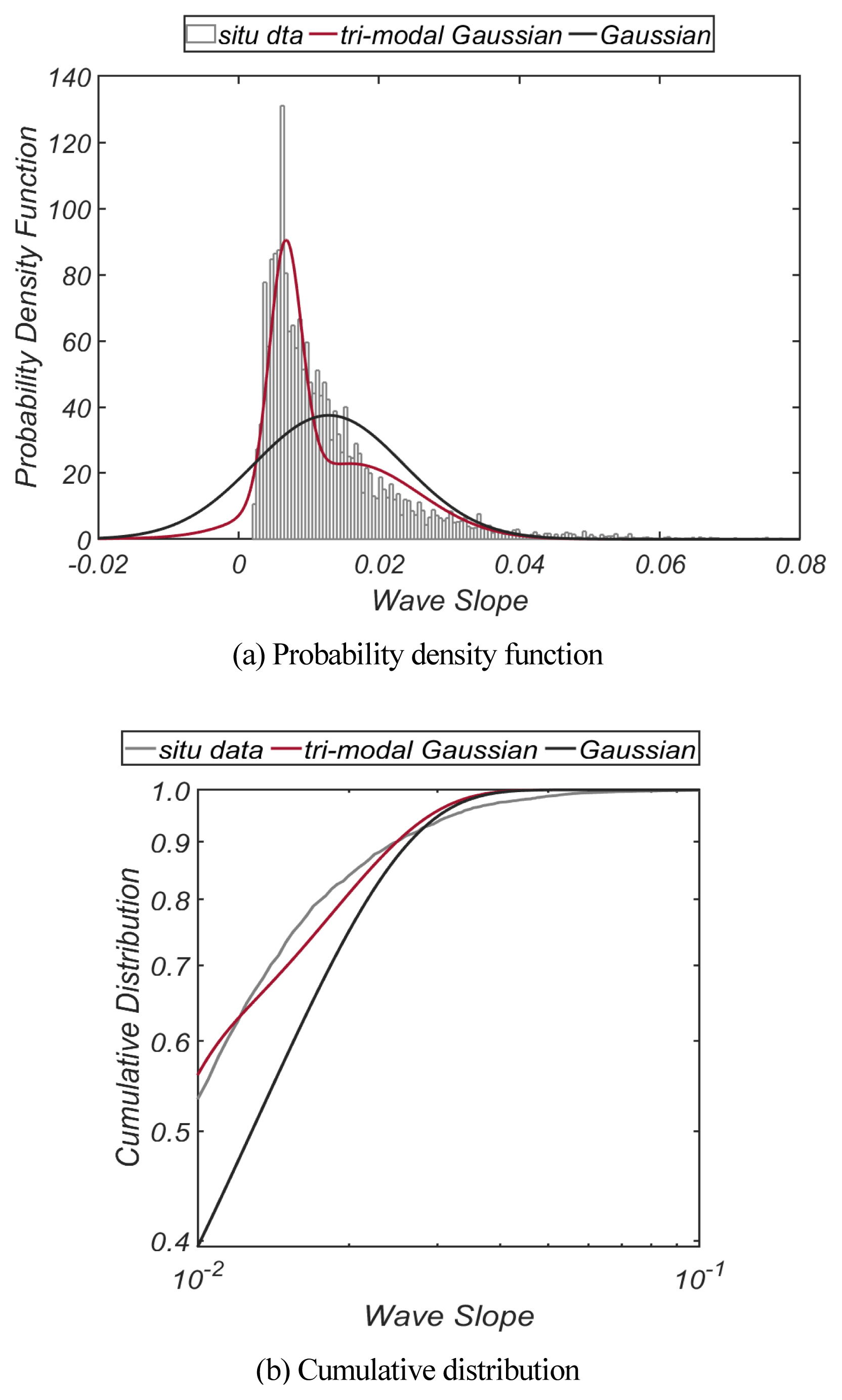
본 절에서는 이러한 어려움을 해결하기 위해 맹방 해빈 전면 해역 수심이 26.5m인 지점[129° 13′ 34.56″ E 37° 27′ 11.22″ N]에서 초음파식 파고계[Nortek]를 활용하여 2017.4.26. ~2018.4.20 사이에 실측된 파랑 관측자료(Cho and Kim, 2019; Cho et al., 2019)로부터 실무에서 더욱 쉽게 활용할 수 있는 확률모형을 제시하려 한다.
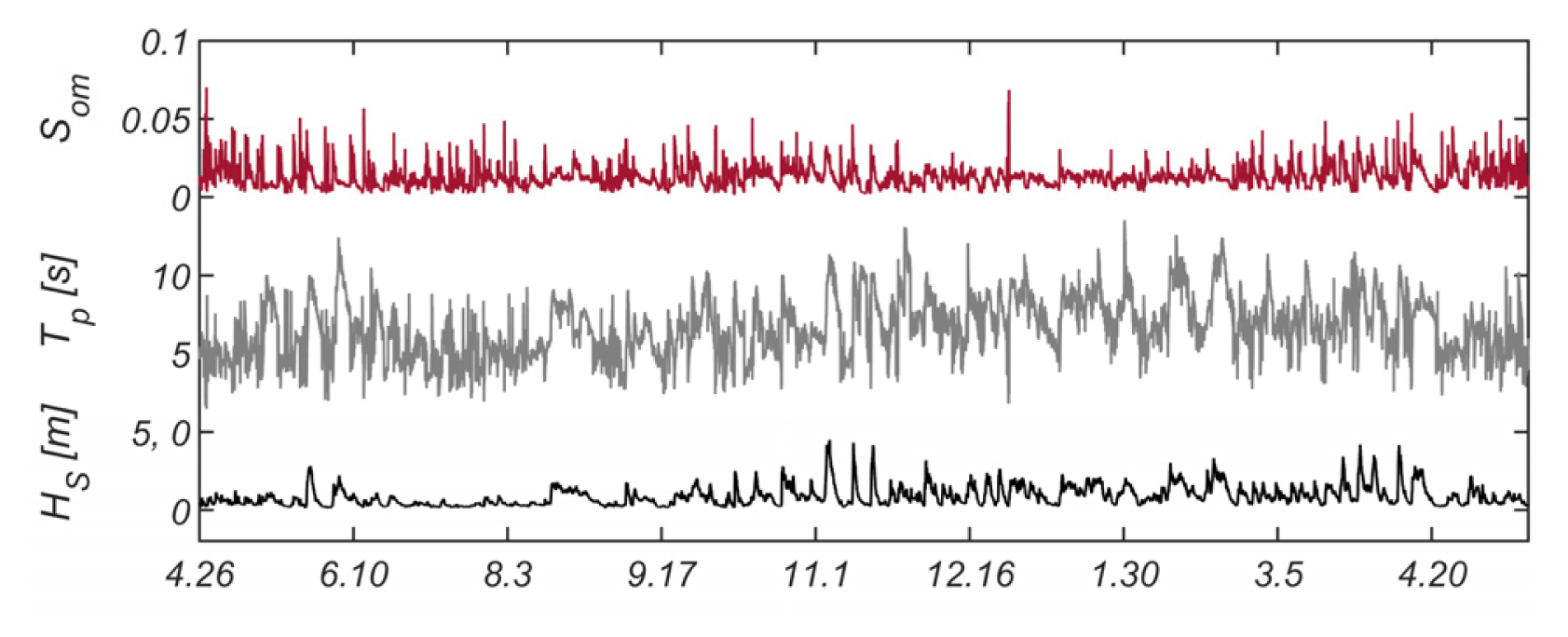
Fig. 9에는 첨두 주기 Tp, 유의 파고 Hs, 파형 경사 Som 의 2017.4.26.부터 2018.4.20.까지의 시계열 자료를 도시하였다.
Fig. 10에는 파형 경사 Som 의 빈도해석 결과를 정리하였으며, 비교를 위해 관측치와 같은 평균과 표준편차를 지니는 Gaussian 분포도 함께 수록하였다. Som = 0.03 인근에 형성되는 확률 고원을 확인할 수 있으며, tri-modal Gaussian 분포를 기저 확률분포로 활용하는 경우 전술한 확률 고원이 상당한 정도로 모의 되는 것을 확인할 수 있다[Fig. 10(a) 참조].
Tri-modal Gaussian 분포는 다음과 같이 정의되며,
여기서 Pi는 weighting coefficient, μi와 σi는 각각 ith 성분 분포의 평균과 표준편차를 나타낸다.
4. Non-Gaussian 파형경사 분포와 Van der Meer 식에 준거한 호안 구조물 피복석 Level III 신뢰성 설계
Van der Geer 식에 기초하여 사석방파제 피복석 강도 R과 파력 S의 차이로 신뢰 함수 Z를 정의하면 Z는 다음과 같이 기술될 수 있으며,
구조물의 신뢰도는 다음과 같이 분류할 수 있다.
엄밀하게 말하면 신뢰 함수 Z는 Nod, Nz, ∆, Dn50, Hs, Som라는 상호 독립적인 6개의 무작위 과정에 종속하나 해석의 편의상 파고 HS과 파형경사 Som 에만 종속하는 것으로 가정하였다.
수치모의는 우리나라 해역별 파랑특성이 피복석 안전에 미치는 영향을 살펴보기 위해, 울산 전면해역, 맹방 전면해역, 울릉도 전면해역을 대상으로 수행하였다[Fig. 12 참조].
4.1 Numerical simulation
4.1.1 울릉도
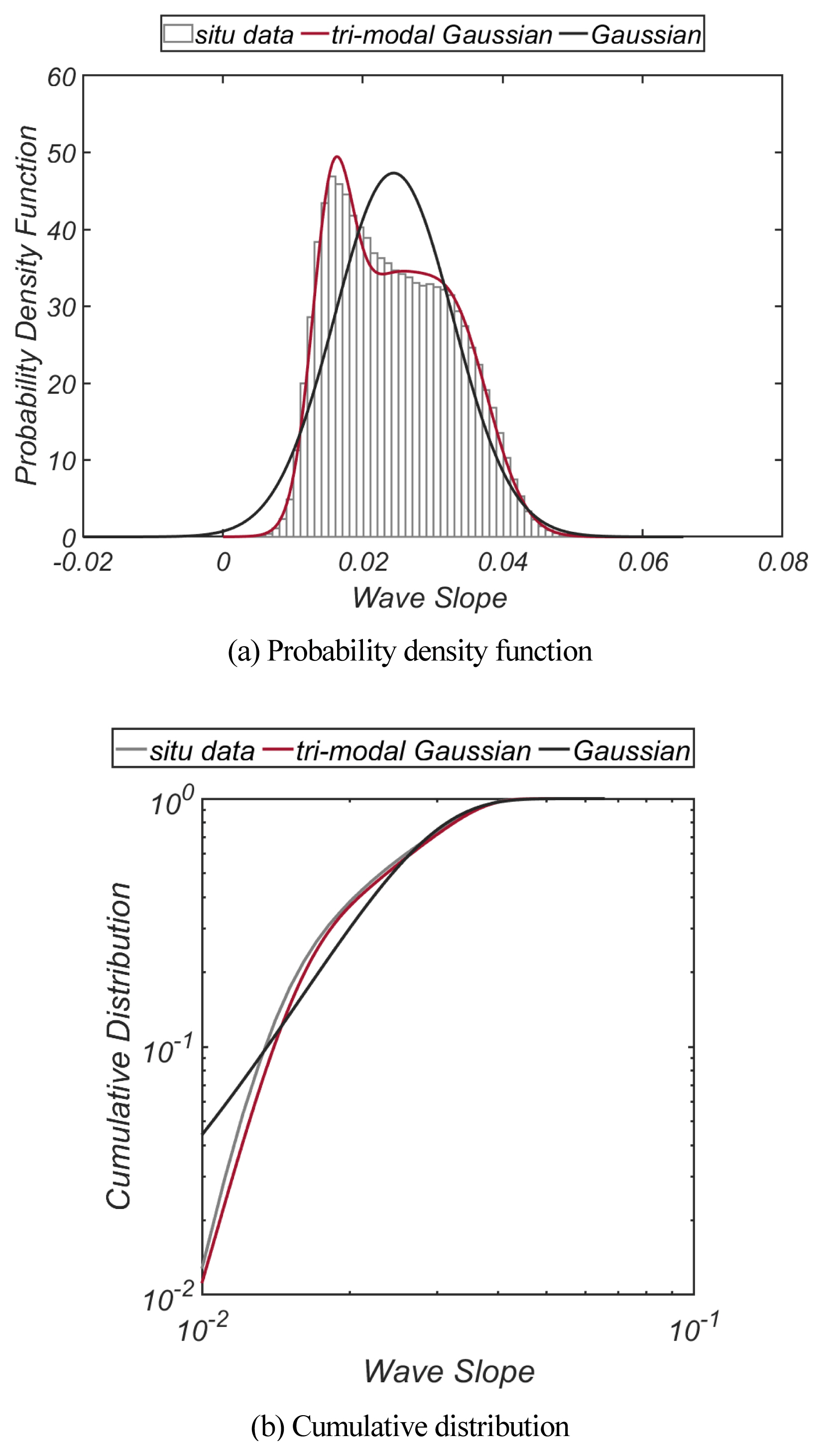
Fig. 13에는 첨두 주기 Tp, 유의 파고 Hs, 파형 경사 Som 의 1979.1.1.부터 2019.12.31까지의 시계열 자료를 도시하였으며, Fig. 14, 15에는 Level III 신뢰성 설계에 필요한 파고 분포와 파형경사 분포를 각각 정리하였다. Fig. 16에는 울릉도 파랑 특성에 대한 이해를 돕기 위해 파고⋅주기 결합분포를 도시하였으며, 을릉도 전면해역의 경우 온화한 해양환경에서 발생하는 외 중력파의 발생확률이 눈에 띄게 낮아 흥미로우며, 이렇게 사라진 외중력파로 인해 파형 경사분포에서 확률 고원은 찾아볼 수 없다. 이러한 현상은 을릉도의 경우 도서 지역의 특성상 자연 해빈에서 흔히 관측되는 tidal terrace가 형성되지 않아 생기는 것으로 보이며[Fig. 17 참조], 이러한 추론은 tidal terrace에서 진행되는 천수과정과 이 과정에서 공진성 wave-wave interaction으로 파랑무리에 출현하는 외중력파의 생성기작을 고려하면 수용 가능해 보인다[Fig. 17 참조].
파고 분포의 경우 two parameter Weibul 분포에서 가장 높은 적합도를 보였으며 two parameter Weibul 분포는 다음과 같이 기술될 수 있다[Fig. 14 참조].
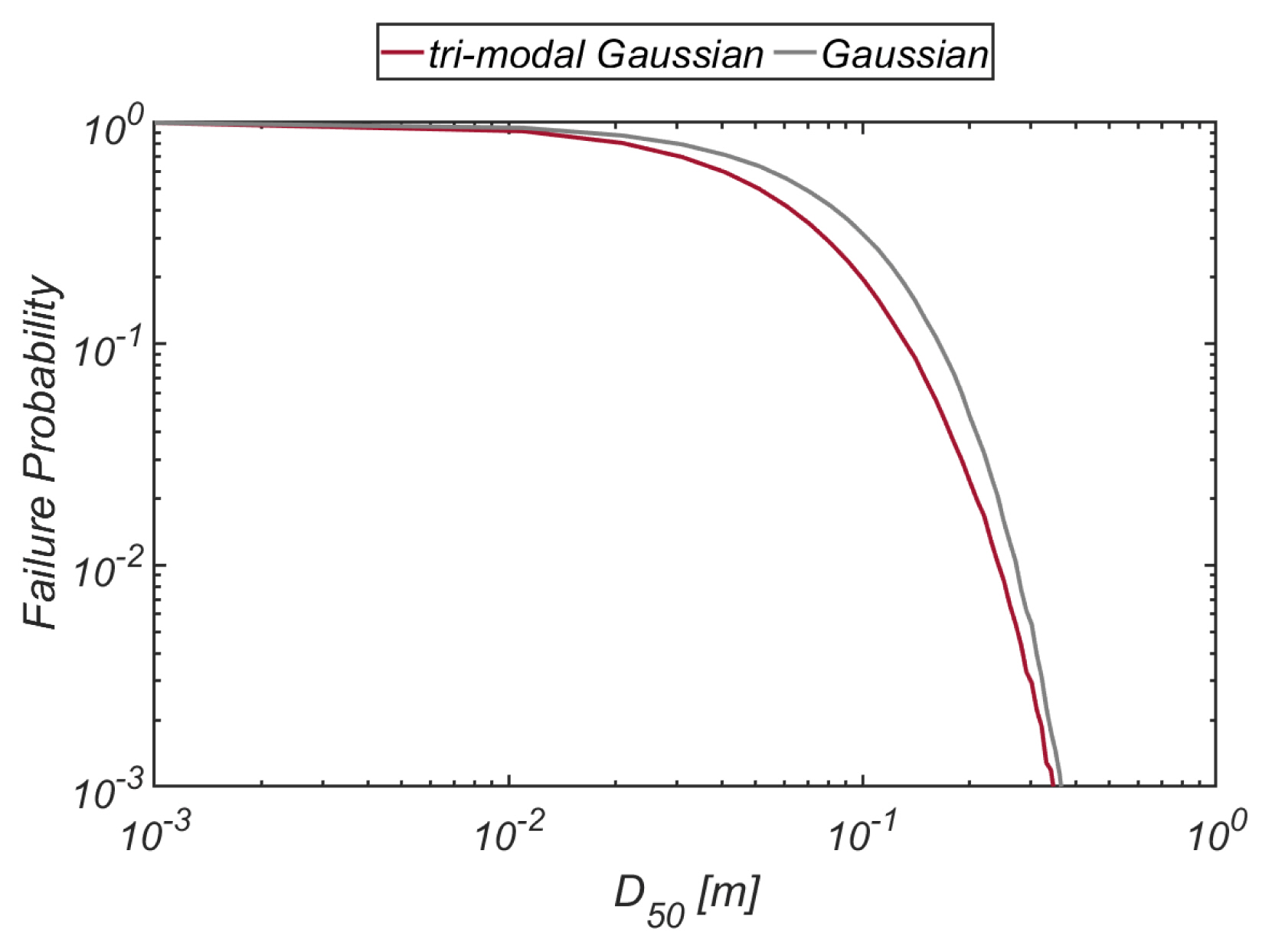
4.1.2 맹방
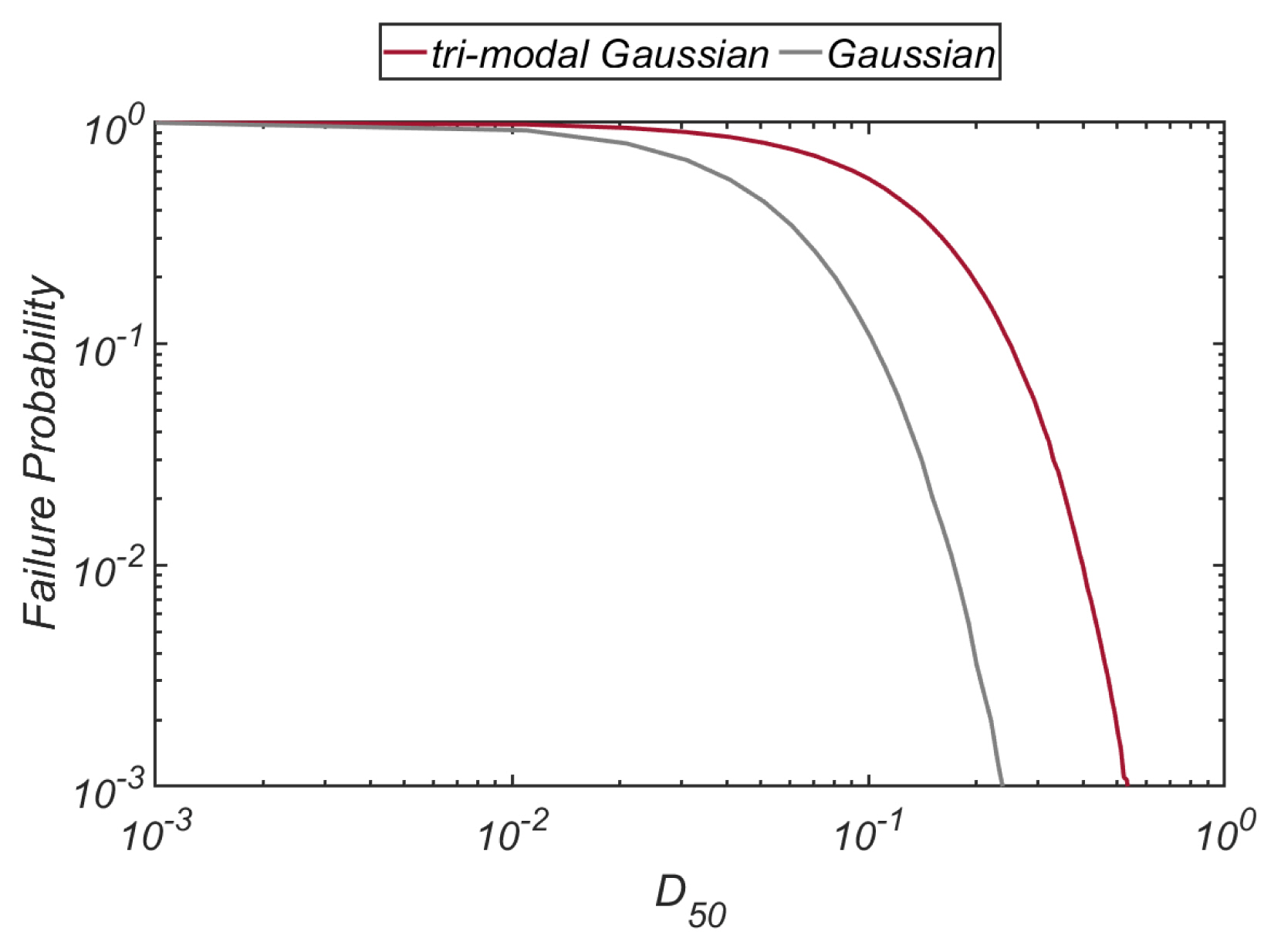
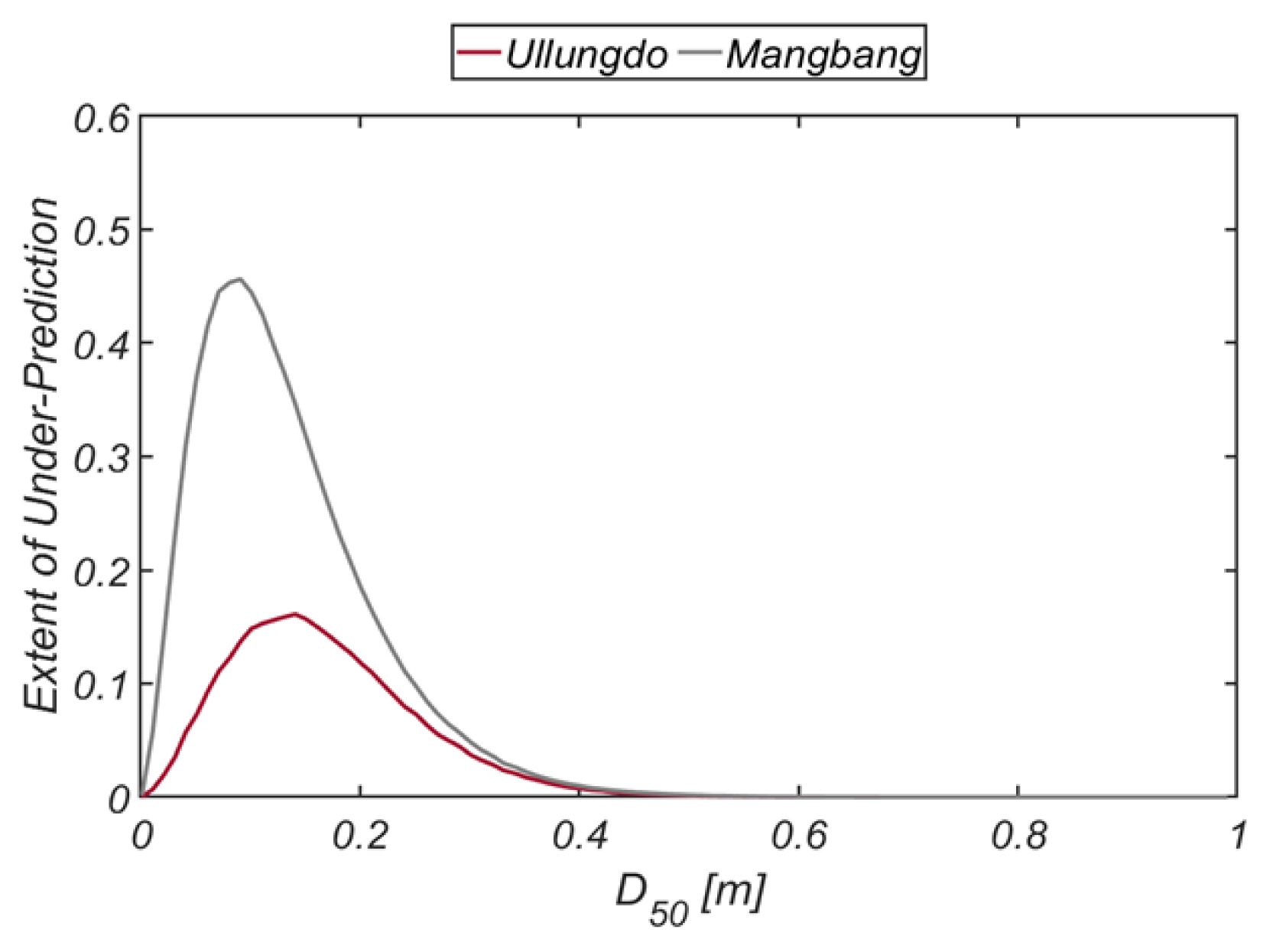
Fig. 19에는 Level III 신뢰성 설계에 필요한 파고 분포를 정리하였으며, Fig. 20에는 피복석 직경에 따른 파괴확률 변화를 정리하였다. 비교를 위해 파형경사가 Gaussian 분포를 추종하는 경우에 대해 모의 된 파괴확률도 함께 수록하였다. Gaussian 분포의 경우 울릉도의 경우와 유사하게 파괴확률이 과소하게 산출되었으며, 과소하게 산출되는 정도는 울릉도보다 증가하는 것이 이채롭다[Fig. 21 참조]. 이러한 현상은 공진성 wave-wave interaction에 의해 파랑 무리에 출현하는 외중력파와 외중력파 출현시 파형경사분포에 형성되는 확률고원의 유무에 따른 차이로 판단되며, 따라서 확률고원은 피복석 파괴확률에 상당한 영향을 미치는 것을 알 수 있다.
이상의 논의를 종합하면, 향후 방파제 외곽시설 신뢰성 설계과정에서 확률고원의 재현이 가능한 tri-modal Gaussian 분포는 상당한 역할을 수행할 것으로 기대된다.
4.1.3 울산
Fig. 22에는 Level III 신뢰성 설계에 필요한 파형경사 분포를 정리하였으며, Fig. 23에는 피복석 직경별 파괴확률을 정리하였다. Fig. 22에서 알 수 있듯 전 절에서 다룬 울릉도, 맹방의 경우와는 매우 다른 파형경사 분포를 확인할 수 있으며, 이러한 차이는 피복석 파괴확률에더 상당한 영향을 미치는 것을 알 수 있다. 울릉도, 맹방의 경우와는 다르게 tri-modal Gaussian 분포가 파괴확률을 과소하게 예측하였다. 이러한 차이는 울산의 경우 Choi and Cho(2019)가 JMA (Japan Meteorological Agency), NOAA(National Oceanic and Atmospheric Administration) 해상풍 자료와 SWAN에 기초한 수치모의 결과로 SWAN 모형에 내재 된 한계에 기인하는 것으로 판단된다.
5. 결 론
불규칙한 해양환경에 거치되는 사석방파제는 거친 해양환경에서도 충분한 내구성을 담보할 수 있도록 설계되어야 하나, 기존 호안 구조물의 피복석은 대부분 Hudson 식 [SPM, 1984]에 의존한 결정론적 기법에 따라 설계됐다. 이러한 설계 관행은 현재 우리나라 항 외곽시설이 지나치게 보수적으로 운영된다는 외부의 평가에서 벗어날 수 없는 결과를 초래하게 된다. 이렇듯 주관적 판단을 강제하는 결정론적 해석의 한계를 해결할 수 있는 대안은 신뢰성 설계로 보이며, 파랑에 내재한 불규칙성을 고려하는 경우 신뢰성 설계는 장기간 관측된 파랑 자료에 기초하여 진행되어야 하나, 우리나라의 경우 현재 장기간에 걸쳐 연속해서 관측된 파랑 자료가 가용하지 않는 경우가 대부분으로 이 경우 유럽 혹은 미국에서 선호되는 확률모형을 단순 수용하여 신뢰성 설계가 수행되는 것으로 보인다 (Kim et al., 2005; Kim et al., 2009; Suh et al., 2003). Van der Meer 식에 기초하는 경우 사석방파제 피복석 파괴 여부를 결정하는 확률변수는 파형 경사와 파고로 보인다. 전술한 확률변수 중 파고의 경우 Rayleigh 분포, 복합 Weibull 분포(Battjes and Groenendijk, 2000), 수정 Glukhovskiy 분포(Klopman and Stive, 1989), 삼 변량 Weibul 분포 등 연구성과가 상당하나, 파형 경사분포는 소홀히 다루어져 현재 Gaussian 분포 (PIANC, 1992), Gram Charlier distribution (Cox and Munk, 1954a; Cox and Munk, 1954b; Cox and Munk, 1956) 등이 가용하나, 파형 경사가 급하거나 해수면 변위가 큰 경우 음의 발생확률을 제시하는 등의 한계를 지닌다. 그러나 최근 Cho (2021)의 연구성과에 따르면 파형 경사는 불규칙 파동 계에 대한 가장 포괄적인 정보를 제공하며, 특히 wave-wave interaction에 의해 파랑 무리에 외중력파가 출현하는 경우 파형 경사분포에는 확률 고원이 형성된다. 이 연구에서 Cho (2021)는 관측자료를 통해 전술한 확률 고원[probability plateau]은 해안선 전진 혹은 후퇴와 밀접하게 연계됨을 예증한 바 있다.
이러한 인식에 기초하여 본연구에서는 Non-Gaussian 파형경사 분포가 항 외곽시설 피복석 안전에 미치는 영향을 수치 모의를 활용하여 살펴보았다. 수치 모의는 Van der Meer 식과 Monte Carlo simulation을 활용한 Level III 신뢰성 설계기법을 활용하여 수행하였다. 이 과정에서 확률모형으로는 파고 분포의 경우 수정 Glukhovskiy 계열 파고 분포, 울릉도 전면해역에서 1979.1.1.~2019.12.31. 사이에 수집된 파고 관측자료를 활용하였다 (Jeong et al., 2018). 파형 경사의 경우 최근 Cho (2021)가 확률변수 변환기법(Papoulis, 1984)을 활용하여 Longuet-Higgins(1983)의 진폭⋅주기 결합 확률분포로부터 해석적으로 유도한 파형 경사분포가 가장 수월성을 지니는 것으로 보인다. 전술한 Non-Gaussian 파형경사 분포를 피복석 신뢰성 설계에 적용하기 위해서는 황천 시 내습하는 파랑의 스펙트럼 bandwidth parameter에 대한 정량적 평가가 선행되어야 하나, 우리나라의 경우 아직 이루어지지 않아 적용을 어렵게 한다. 이러한 어려움을 해결하기 위해 맹방 해빈 전면해역 수심이 26.5m인 지점[129° 13′ 34.56″ E 37° 24′ 11.22″ N]에서 초음파식 파고계[Nortek]를 활용하여 2017.4.26.~2018.4.20 사이에 실측된 파랑 관측자료(Cho and Kim, 2019; Cho et al., 2019)로부터 파형경사 분포를 산출하였다. 이 과정에서 천수과정에서의 공진선 wave-wave interaction으로 인해 파동계에 외중력파가 출현하는 경우 파형경사 분포에는 확률 고원[probability plateau]이 생성되는 것을 확인하였다.
이처럼 확률 고원[probability plateau]이 생성되는 경우 여러 확률분포를 기저 분포로 활용한 검증 과정에서 Tri-modal Gaissuian 분포가 가장 우월한 적합도를 보였다. 이 과정에서 Tri-modal Gaussian분포의 확률모수는 Matlab 기반 Statistics and Machine Learning Toolbox 중 MLE[Maximum Likelihood Estimates]를 활용하여 산출하였다. 모의 결과 Gaussian 분포는 음의 파형경사에도 작지 않은 확률 질량을 부과하는 등 한계를 보였으며, 길고 짧은 파랑 대역에서의 under-shooting, 중간규모 파랑 대역에서의 over-shooting 등의 오류도 확인하였다. 사석방파제 피복석 파괴확률의 경우 Gaussian 분포는 파괴확률이 과소하게 산출되는 것으로 모의 되었으며, 과소하게 산출되는 정도는 울릉도보다 수심이 낮고 완만하게 변하는 tidal terrace가 발달한 맹방에서 증가하였다. 이러한 현상은 공진성 wave-wave interaction에 의해 파랑 무리에 출현하는 외 중력파와 외중력파 출현 시 파형 경사분포에 형성되는 확률 고원의 유무에 따른 차이로 판단되며, 따라서 확률 고원은 피복석 파괴확률에 상당한 영향을 미치는 것을 알 수 있다.
이상의 논의를 종합하면, 먼저 파동계에 내재한 비선형성을 설명할 수 있는 어떠한 기제도 지니지 못한 단순 선형모형인 Gaussian 파형경사 분포(PIANC, 1992)는 우리나라 해양환경과는 상당한 거리가 존재하는 것을 알 수 있다(Cho, 2021). 또한 situ wave data에서 확인되듯 반시계 방향으로 틀어져 풍성파 발달에 필요한 취송거리가 미국 혹은 유럽과는 달리 제한적인 방위에서만 확보되는 동해에 노출되는 우리나라 동해안의 경우 상당한 다양한 성격의 파랑이 관측된다. 따라서 전술한 해양환경을 담아낼 수 있는 기제를 지닌 Tri-modal Gaussian 파형 경사분포는 괜찮은 대안으로 판단된다. 전술한 Tri-modal Gaussian 파형경사 모형의 수월성은 천수과정에서 파동무리에 외중력파가 출현하는 경우 주기가 긴 외중력파의 성정으로 인해 파형 경사분포에 형성되는 확률고원의 기술이 가능하다는 사실에서 확인할 수 있다.
전술한 사실에 비추어보면 향후 방파제 외곽시설 신뢰성 설계과정은 파랑에 내재한 비선형성을 기술할 수 있는 Tri-modal Gaussian 파형 경사분포가 방파제 외곽시설 신뢰성 설계과정에 활용되는 경우 보다 효율적인 설계가 가능하리라 판단된다.










 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print