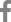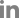1. ņä£ ļĪĀ
15ņäĖĻĖ░ ņżæņŚĮņŚÉ ļīĆĒĢŁĒĢ┤ ņŗ£ļīĆĻ░Ć ņŗ£ņ×æļÉĀ ļ¼┤ļĀĄ Ļ▒░ņ╣£ ĒĢ┤ņ¢æĒÖśĻ▓Įņ£╝ļĪ£ļČĆĒä░ ņ×Éņ£ĀļĪ£ņÜ┤ ņĀĢņś©ĒĢ£ ĒĢ┤ņŚŁņØä ņ¢╗ņ£╝ļĀżļŖö ņØĖļźśņØś ļģĖļĀźļÅä ĒĢ©Ļ╗ś ņŗ£ņ×æļÉÉņ£╝ļ®░, ņØ┤ļ¤¼ĒĢ£ ļģĖļĀźņ£╝ļĪ£ ņ×ÉņŚ░ņŚÉņä£ ņēĮĻ▓ī ņ¢╗ņØä ņłś ņ׳ļŖö ņé¼ņäØņØä ĒÖ£ņÜ®ĒĢ£ ņ┤łĻĖ░ĒśĢĒā£ņØś ņé¼ņäØ ļ░®ĒīīņĀ£Ļ░Ć ņÖäņä▒ļÉ£ļŗż. Ēł¼ņäØņ£╝ļĪ£ ņĪ░ņä▒ļÉ£ ņé¼ņäØ Ļ▓Įņé¼ņĀ£ļŖö Ēīīļ×æ ņŚÉļäłņ¦ĆĻ░Ć ņ¦æņżæļÉśļŖö ĒÅēĻĘĀĒĢ┤ņłśļ®┤Ļ│╝ ņØ┤ņøāĒĢ£ ņé¼ļ®┤ņŚÉņä£ ņ¦äĒ¢ēļÉśļŖö ņćäĻĄ┤ļĪ£ ļ│ĆĒśĢļÉśļ®░ ņóģĻĄŁņŚÉļŖö ĒÅēĻĘĀĒĢ┤ņłśļ®┤ ņØĖĻĘ╝ņŚÉ ļŗ©ņØ┤ ĒśĢņä▒ļÉ£ļŗż. ņØ┤Ēøä ņé¼ņäØ Ļ▓Įņé¼ņĀ£ļŖö ņĢłņĀĢĒÖö ļŗ©Ļ│äņŚÉ ņ¦äņ×ģĒĢśņŚ¼ ņāüļŗ╣ ĻĖ░Ļ░ä ņČöĻ░ĆņĀüņØĖ ļ│ĆĒśĢņŚåņØ┤ ļ░®ĒīīņĀ£ļĪ£ ĻĖ░ļŖźĒĢśņŚ¼ ņÖöļŗż. ņØ┤ļŖö Ēīīļ×æņŚÉ ļīĆĒĢ£ ļé┤ĻĄ¼ņä▒ņØ┤ ņłśņøöĒĢ£ ļ░®ĒīīņĀ£ ļŗ©ļ®┤ ĒśĢĒā£ļź╝ ņÜ░ļ”¼ņŚÉĻ▓ī ņŗ£ņé¼ĒĢśļ®░ ņĪ░ņä▒ļŗ©Ļ│äļČĆĒä░ ĒÅēĻĘĀĒĢ┤ņłśļ®┤ ņØĖĻĘ╝ņŚÉ ļŗ©ņØä ļ░░ņ╣śĒĢśļŖö berm breakwaterļŖö Ļ░ÖņØĆ ļ¦źļØĮņ£╝ļĪ£ ĒĢ┤ņäØļÉĀ ņłś ņ׳ļŗż(Woo, 2016). ļ░®ĒīīņĀ£ļŖö ņĪ░ņäĀ ĻĖ░ņłĀņØś ļ░£ņĀäĻ│╝ Ēīīļ×æņŚÉ ļīĆĒĢ£ ņÜ░ļ”¼ņØś ņØ┤ĒĢ┤Ļ░Ć Ļ╣Ŗņ¢┤ņ¦ÉņŚÉ ļö░ļØ╝ ļŗżņ¢æĒĢ£ ĒśĢĒā£ļĪ£ ņ¦äĒÖöĒĢ£ļŗż. ņ¦ĆĻĖłĻ╣īņ¦Ć ņĀ£ņŗ£ļÉ£ ņŚ¼ļ¤¼ ĒśĢĒā£ņØś ļ░®ĒīīņĀ£ ņżæ ļé┤ņŖĄĒĢśļŖö Ēīīļ×æņŚÉļäłņ¦ĆņØś ņåīņé░ņØ┤ļ×Ć Ļ┤ĆņĀÉņŚÉņä£ ļ│┤ļ®┤ ņé¼ņäØ Ļ▓Įņé¼ņĀ£Ļ░Ć Ļ░Ćņן ĒÜ©ņ£©ņĀüņØ┤ļéś ņäØņ×¼ļź╝ ņ¢╗ĻĖ░ ņ£äĒĢ£ ņ▒äņäØĻ│╝ņĀĢņŚÉņä£ ļ░£ņāØĒĢśļŖö ĒÖśĻ▓ĮĒø╝ņåÉņ£╝ļĪ£ ņØĖĒĢ┤ ņĄ£ĻĘ╝ ļōżņ¢┤ ļīĆĒśĢ ņ╝ĆņØ┤ņŖ©ņØä ĒÖ£ņÜ®ĒĢ£ ņ¦üļ”ĮņĀ£Ļ░Ć ņŻ╝ļźśļź╝ ņØ┤ļŻ¼ļŗż. ĒĢ┤ņāüņØä ĒåĄĒĢ£ ļ¼╝ļÅÖļ¤ēņØś ņ”ØĻ░ĆņÖĆ ņØ┤ļĪ£ ņØĖĒĢ£ ņäĀļ░ĢņØś ļīĆĒśĢĒÖöļĪ£ Ēśäņ×¼ ņ¦üļ”ĮņĀ£ļŖö ņłśņŗ¼ 20~25mņØĖ ņłśņŚŁņŚÉ ņĪ░ņä▒ļÉśļ®░, ņé¼ņäØ Ļ▓Įņé¼ņĀ£ņÖĆ Ļ▓¼ņżäļ¦īĒĢ£ ņŚÉļäłņ¦Ć ņåīņé░ĒÜ©Ļ│╝ļź╝ ņ¢╗ĻĖ░ ņ£äĒĢ┤ ņ£Āņłśņŗż, ņŖ¼ļ”┐ ļō▒ņØ┤ ņł£ņ░©ņĀüņ£╝ļĪ£ ļÅäņ×ģļÉśļ®░ ņ¦äĒÖöĒĢśņśĆļŗż. ĻĘĖļ¤¼ļéś ņĀäņłĀĒĢ£ ņ£Āņłśņŗż, ņŖ¼ļ”┐ ļō▒ņØĆ ņ£ĀņłśņŗżņŚÉ ĒżĒÜŹļÉ£ Ļ│ĄĻĖ░ņĖĄņØ┤ ņØ┤ņÖäŌŗģņĢĢņČĢļÉśļ®░ ņāØņä▒ļÉśļŖö Ēīīļ×æņ£╝ļĪ£ ņØĖĒĢ┤ ļ¬®ņĀüĒĢ£ ņŚÉļäłņ¦Ć ņåīņé░ĒÜ©Ļ│╝Ļ░Ć ĒÜ©Ļ│╝ņĀüņ£╝ļĪ£ ĻĄ¼ĒśäļÉśņ¦Ć ļ¬╗ĒĢśļŖö Ļ▓ĮņÜ░ļÅä ņāüļŗ╣ĒĢśļ®░ ņØ┤ Ļ▓ĮņÜ░ ņāüļŗ╣ĒĢ£ ļ░śņé¼Ļ░Ć ņ¦äĒ¢ēļÉĀ ņłś ņ׳ļŗż(Woo, 2016). Ēīīļ×æņØ┤ ņ¦üļ”Į ļ░®ĒīīņĀ£ņŚÉ ļ╣äņŖżļō¼Ē׳ ļé┤ņŖĄĒĢśļŖö Ļ▓ĮņÜ░ ņ×ģņé¼Ēīī, ļ░śņé¼ĒīīņÖĆ ļŹöļČłņ¢┤ ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēĒĢśļŖö ņŚ░ĒīīĻ░Ć ņāØņä▒ļÉśļ®░, ņØ┤ļĀćĻ▓ī ņāØņä▒ļÉ£ ņŚ░ĒīīļŖö ņāüļŗ╣ĒĢ£ ņ¢æņØś ņøöĒīīļź╝ ņ┤łļלĒĢĀ ņłś ņ׳ņ¢┤ ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēĒĢśļŖö ņŚ░ĒīīņØś ĒÜ©Ļ│╝ņĀü ņĀ£ņ¢┤ļŖö ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņä▒ļŖźņØä Ļ▓░ņĀĢĒĢśļŖö ņżæņÜöĒĢ£ ņäżĻ│ä ņØĖņ×ÉļĪ£ ĒīÉļŗ©ļÉ£ļŗż[Fig. 1, 2 ņ░ĖņĪ░](Woo, 2016).
ņŚ░ĒīīļŖö Perroud(1957), Chen(1961) ļō▒ņØ┤ ņ▓£ĒĢ┤ņŚŁņŚÉņä£ ņןĒīīļź╝ ļīĆņāüņ£╝ļĪ£ ņłśĒ¢ēĒĢ£ ņłśļ”¼ ļ¬©ĒśĢņŗżĒŚśņŚÉņä£ ņ▓śņØīņ£╝ļĪ£ Ļ┤ĆņĖĪļÉśņŚłņ£╝ļ®░ ĻĘĖ Ēøä Wiegel(1964 a, b)ņØĆ ņ¦üļ”ĮņĀ£ņŚÉ Ļ│Āļ”ĮĒīīĻ░Ć ļ╣äņŖżļō¼Ē׳ ņ×ģņé¼ĒĢśļŖö Ļ▓ĮņÜ░ ņŚ░ĒīīĻ░Ć ĒśĢņä▒ļÉśļŖö Ļ▓āņØä Ļ┤ĆņĖĪĒĢ£ ļ░ö ņ׳ļŗż. Wiegel(1964 a, b)ņŚÉ ļö░ļź┤ļ®┤ ņ×ģņé¼Ļ░üņØ┤ 45┬░ ļ│┤ļŗż ņ×æņØĆ Ļ▓ĮņÜ░ ņ×ģ, ļ░śņé¼Ēīī ņÖĖņŚÉ ņŚ░ĒīīĻ░Ć ņČ£ĒśäĒĢśĻĖ░ ņŗ£ņ×æĒĢśļ®░ ņ×ģņé¼Ļ░üņØ┤ 20┬░ ļ│┤ļŗż ņ×æņØĆ Ļ▓ĮņÜ░ņŚÉļŖö ļ░śņé¼ĒīīļŖö ņé¼ļØ╝ņ¦ĆĻ│Ā ņŚ░Ēīīļ¦īņØ┤ ņĪ┤ņ×¼ĒĢ£ļŗż. ņØ┤Ēøä Nielsen(1962), BergerņÖĆ Kohlhase(1976)ļŖö ņ▓£ņØ┤ņŚŁņŚÉņä£ ļ╣äņŖżļō¼Ē׳ ņ×ģņé¼ĒĢśļŖö ĻĘ£ņ╣Ö Ēīīļź╝ ļīĆņāüņ£╝ļĪ£ ņłśĒ¢ēļÉ£ ņłśļ”¼ļ¬©ĒśĢņŗżĒŚśņŚÉņä£ļÅä Ļ│Āļ”ĮĒīīņØś Ļ▓ĮņÜ░ņÖĆ ņ£Āņé¼ĒĢ£ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņØĆ ļ░ö ņ׳ļŗż. Nielsen(1962), BergerņÖĆ Kohlhase(1976) ļō▒ņŚÉ ļö░ļź┤ļ®┤ ņŚ░ĒīīņØś ĒīīĻ│ĀļŖö ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņĀÉĻĘ╝ņĀüņ£╝ļĪ£ ņ”ØĻ░ĆĒĢśļŗż ņØ╝ņĀĢĒĢ£ Ļ░Æņ£╝ļĪ£ ņłśļĀ┤ĒĢśļ®░ ņŚ░ĒīīņØś ĒīīĻ│ĀļŖö ņ×ģņé¼Ļ░üĻ│╝ ņłśņŗ¼ņØ┤ Ļ░Éņåī ļÉ©ņŚÉ ļö░ļØ╝ ņ”ØĻ░ĆĒĢśļ®░ ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņŚ░ĒīīĻ░Ć ņāØņä▒ļÉśļŖö ņśüņŚŁņØś ĒÅŁņØĆ ņ×ģņé¼ĒīīņØś ņŻ╝ĻĖ░Ļ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ĒÖĢļīĆļÉ£ļŗż. ļśÉĒĢ£ ņ×ģņé¼Ēīī ĒīīĻ│ĀĻ░Ć ņŚ░ĒīīņØś ņāØņä▒ ĒŖ╣ņä▒ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņŚÉ ļīĆĒĢ┤ņä£ļŖö Stokes Ēīīļ×æņØś ļČłņĢłņĀĢņä▒ ļō▒ņ£╝ļĪ£ ņŗżĒŚśņŚÉ ļö░ļØ╝ ņĀĢļÅäņØś ņ░©ņØ┤ļŖö ņ׳ņ£╝ļéś ņ×ģņé¼ ĒīīĻ│ĀĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ņŚ░Ēīī ĒīīĻ│ĀļŖö Ļ░ÉņåīļÉśļ®░ ņŚ░Ēīī ļ░£ņāØ ņśüņŚŁņØś ĒÅŁņØĆ ņ”ØĻ░ĆĒĢ£ļŗż.
ņØ┤Ēøä Melville(1980)ņØĆ ļ╣äņŖżļō¼Ē׳ ņ×ģņé¼ļÉśļŖö Ļ│Āļ”ĮĒīīņŚÉ ņØśĒĢ┤ ņĢ╝ĻĖ░ļÉśļŖö ņŚ░Ēīīļź╝ ļīĆņāüņ£╝ļĪ£ ņĀĢĻĄÉĒĢ£ ņłśļ”¼ļ¬©ĒśĢ ņŗżĒŚśņØä ņłśĒ¢ēĒĢśņŚ¼ ņ×ģņé¼ĒīīĻ│ĀņÖĆ ņ×ģņé¼Ļ░üļÅäĻ░Ć ņŚ░ĒīīņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņŚÉ ļīĆĒĢ┤ ĻĘ£ļ¬ģĒĢ£ ļ░ö ņ׳ļŗż. Melville(1980)ņŚÉ ņØśĒĢśļ®┤ Ēīīļ×æņØ┤ ņ¦äĒ¢ēļÉśļ®┤ņä£ ņŚ░Ēīī ĒÅŁņØĆ ņ”ØĻ░ĆĒĢśļ®░ ņŚ░Ēīī ĒīīĻ│ĀļŖö ņ×ģņé¼Ēīīļ│┤ļŗżļŖö Ēü¼ļéś ņ×ģņé¼ĒīīĻ│ĀņØś ļæÉ ļ░░ļź╝ ņāüĒÜīĒĢśļŖö Ļ▓āņØĆ ņĢäļŗłļ®░, ņ×ģņé¼ Ļ░üļÅäĻ░Ć ņ×æņØäņłśļĪØ ņŚ░ĒīīņØś ĒīīĻ│ĀļŖö Ļ░ÉņåīĒĢ£ļŗż. ļśÉĒĢ£ ņØ┤ļ¤¼ĒĢ£ Ļ▓ĮĒ¢źņØĆ ņ×ģņé¼ Ēīīļ×æņØś ĒīīĻ│Ā ņ”ē, ļ╣äņäĀĒśĢņä▒ņØ┤ Ēü┤ņłśļĪØ ļŹöņÜ▒ ļÜ£ļĀĘĒĢśĻ▓ī ļéśĒāĆļé£ļŗż. ņØ┤ņŚÉ ļ░śĒĢ┤ Nielsen(1962), BergerņÖĆ Kohlhase(1976) ļō▒ņØĆ ņ¦üļ”ĮņĀ£ņŚÉ ļ╣äņŖżļō¼Ē׳ ņ×ģņé¼ļÉśļŖö ņĀĢĒśäĒīīņØś Ļ▓ĮņÜ░ņŚÉļÅä ņŚ░ĒīīĻ░Ć ĒśĢņä▒ļÉĀ ņłś ņ׳ņØīņØä ņŗżĒŚśņ£╝ļĪ£ ņ×ģņ”ØĒĢśņśĆļŗż. ņĀĢĒśäĒīīņŚÉ ņØśĒĢ┤ ņĢ╝ĻĖ░ļÉśļŖö ņŚ░ĒīīĒīīļ×æņØś ĒŖ╣ņä▒ņØĆ Ļ│Āļ”ĮĒīīņŚÉ ļīĆĒĢ£ MelvilleņØś Ļ┤ĆņĖĪņ╣śņÖĆ ļīĆņ▓┤ļĪ£ ņØ╝ņ╣śĒĢśļéś ņ×ģņé¼ ĒīīĻ│ĀĻ░Ć ņŚ░Ēīī ĒīīĻ│ĀņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØĆ Ļ┤ĆņĖĪĒĢśņ¦Ć ļ¬╗ĒĢśņśĆļŗż. ņĄ£ĻĘ╝ Mase (2002)ļŖö ļŗ©ņł£ ņ¦üļ”ĮņĀ£ņÖĆ ļČłĻĘ£ņ╣Ö Ēīīļ×æņØä ļīĆņāüņ£╝ļĪ£ ņłśĒ¢ēļÉ£ ņłśļ”¼ļ¬©ĒśĢņŗżĒŚśņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ņŚ░Ēīī ĒĢ┤ņäØņØä ļČłĻĘ£ņ╣Ö ĒīīļÅÖĻ│äļĪ£ ĒÖĢļīĆĒĢśņśĆļŗż. Mase (2002)ņØś ņŚ░ĻĄ¼ ņä▒Ļ│╝ņŚÉ ļö░ļź┤ļ®┤ ļČłĻĘ£ņ╣Ö ĒīīļÅÖĻ│äņŚÉņä£ļÅä ņäĀĒśĢ ĒīīļÅÖĻ│äņÖĆ ņ£Āņé¼ĒĢ£ ņä▒ņĀĢņØś ņŚ░ĒīīĻ░Ć Ļ┤ĆņĖĪļÉśļéś, ņŚ░ĒīīĻ░Ć ņāØņä▒ļÉśļŖö Ļ│ĄĻ░äņĀü ņśüņŚŁņØĆ ļ╣äņäĀĒśĢ ņĀĢļÅäņŚÉ ņāüĻ┤ĆņŚåņØ┤ ĻĘĀņØ╝ĒĢśĻ▓ī ņ£Āņ¦ĆļÉ£ļŗż.
ņŚ░Ēīī ĒĢ┤ņäØņØä ņ£äĒĢ£ Ēīīļ×æ ļ¬©ĒśĢņØĆ ņłśņŗ¼ņØ┤ ņØ╝ņĀĢĒĢ£ ņ▓£ņØ┤ņŚŁņØś Ļ▓ĮņÜ░ Yue and Mei(1980)ņŚÉ ņØśĒĢ┤ Stokes Ēīīļ×æ ņØ┤ļĪĀĻ│╝ WKB ĻĘ╝ņé¼ļ▓ĢņŚÉ ĻĖ░ņ┤łĒĢśņŚ¼ ņĀ£ņŗ£ļÉ£ ļ░ö ņ׳ļŗż. ņØ┤ ņŚ░ĻĄ¼ņŚÉņä£ Yue and Mei(1980)ļŖö ņäŁļÅÖļ▓ĢņŚÉņä£ ļÅäņ×ģļÉ£ Ļ│Āņ░© ļ│┤ņĀĢ ĒĢŁņØä ļīĆņāüņ£╝ļĪ£ ĒĢ£ ļ╣äņĀ£ņ░© ļ»ĖļČä ļ░®ņĀĢņŗØņØś ĒŖ╣ņłśĒĢ┤Ļ░Ć ņĪ┤ņ×¼ĒĢśĻĖ░ ņ£äĒĢ┤ ņČ®ņĪ▒ņŗ£ņ╝£ņĢ╝ ĒĢśļŖö ņĪ░Ļ▒┤ņØĖ Solvability Conditionņ£╝ļĪ£ļČĆĒä░ ļ│Ąņåīņłś ņ¦äĒÅŁņØä ĻĖ░ņłĀĒĢśļŖö ĻĖ░ļ│Ė ļ░®ņĀĢņŗØņØä ņ£ĀļÅäĒĢśņśĆļŗż. ļśÉĒĢ£ Yue and Mei(1980)ļŖö Ēżļ¼╝ĒśĢ ĻĘ╝ņé¼ļź╝ ņĀüņÜ®ĒĢśļ®┤ ņĀäņłĀĒĢ£ ĻĖ░ļ│Ė ļ░®ņĀĢņŗØņØĆ ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņ£╝ļĪ£ ņĀäĒÖśļÉśļ®░ ņØ┤ Ēīīļ×æ ļ¬©ĒśĢņŚÉ ĻĖ░ņ┤łĒĢśļ®┤ ņĀäņłĀĒĢ£ Stokes Ēīīļ×æņŚÉ ļīĆĒĢ£ ņŚ░Ēīī ņāØņä▒ ĒŖ╣ņä▒ņØä ņ¢┤ļŖÉ ņĀĢļÅä ņ×¼ĒśäĒĢĀ ņłś ņ׳ņØīņØä ņśłņ”ØĒĢ£ ļ░ö ņ׳ļŗż. ņØ┤Ēøä Kirby and Dalrymple(1983)ņØĆ ļŗżņ░©ņøÉ ņäŁļÅÖļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ Yue and Mei(1980)ņØś Ēīīļ×æ ļ¬©ĒśĢņØä ņÖäļ¦īĒĢ£ ņłśņŗ¼ ļ│ĆĒÖöĻ░Ć ņĪ┤ņ×¼ĒĢśļŖö ņ▓£ņØ┤ņŚŁņŚÉļÅä ņĀüņÜ®ĒĢĀ ņłś ņ׳ļÅäļĪØ ņØ╝ļ░śĒÖöĒĢśņśĆļŗż. ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØĻ│╝ ņ×ÉņŚ░ ĒĢśņ▓£ņŚÉņä£ņØś ļÅäņłś ĒśäņāüņŚÉ ļīĆĒĢ£ ņ¦Ćļ░░ ļ░®ņĀĢņŗØ Ļ░äņØś ņ£Āņé¼ņä▒ņØä ĒåĀļīĆļĪ£ ņŚ░ĒīīļŖö ņäĀĒśĢ ņØ┤ļĪĀņØś ļŗ©ņł£ ņäØĻ▓Į ļ░śņé¼ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö Ļ│ĄņĢĪ ņāüĒā£ļĪ£ņØś ļČłņŚ░ņåŹņĀüņØĖ ņĀäņØ┤ļĪ£ ĒĢ┤ņäØĒĢ£ Peregrine(1983)ņØś ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ņŚÉ ĻĘ╝Ļ▒░ĒĢśļ®┤ ņŚ░ĒīīļŖö ņ×ģņé¼ĒīīņÖĆ ļ░śņé¼Ēīī Ļ░äņØś Ļ│Ąņ¦äņä▒ ņāüĒśĖņ×æņÜ®ņŚÉ ļö░ļØ╝ ņ¦üļ”ĮņĀ£ ļ░®Ē¢źņ£╝ļĪ£ ņ¦äĒ¢ēĒĢśļŖö ņĀ£4ņØś Ēīīļ×æ ņä▒ļČäņ£╝ļĪ£ Ēīīļ×æ ņŚÉļäłņ¦ĆĻ░Ć ņĀäņØ┤ļÉśļŖö Ēśäņāüņ£╝ļĪ£ ļ│┤ņØĖļŗż.
ņĀäņłĀĒĢ£ ņŚ░ĻĄ¼ņŚÉņä£ Yue and Mei(1980), Kirby and Dalrymple (1983)ņØĆ ĒÜ©ņ£©ņĀüņØĖ ņłśņ╣ś ņŚ░ņé░ņØä ņ£äĒĢ┤ Ēżļ¼╝ĒśĢ ĻĘ╝ņé¼ļź╝ ņĀüņÜ®ĒĢśņŚ¼ ņ×ģņé¼ Ļ░üļÅäņŚÉ ļŗżņåī ņĀ£ņĢĮņØä ļ░øļŖö ļŗ©ņĀÉņØ┤ ņ׳ļŗż. ņ▓£ĒĢ┤ņŚŁņØś Ļ▓ĮņÜ░ ņĄ£ĻĘ╝ Kirby(1990)ļŖö ņ▓£ĒĢ┤ņŚŁņŚÉņä£ņØś ļīĆĒæ£ņĀüņØĖ Ēīīļ×æ ļ¬©ĒśĢņØĖ Boussinesq ļ░®ņĀĢņŗØĻ│╝ Ēīīļ×æņØ┤ ņŗ£Ļ░äĻ│╝ ņŻ╝ ņ¦äĒ¢ē ļ░®Ē¢źļ┐Éļ¦ī ņĢäļŗłļØ╝ ņŚ░ņĢł ļ░®Ē¢źņ£╝ļĪ£ļÅä ņŻ╝ĻĖ░ņĀüņØĖ Ļ▒░ļÅÖņØä ļ│┤ņØĖļŗżļŖö Ļ░ĆņĀĢĒĢśņŚÉ ļ¼┤ņ×æņ£ä Ēīīļ×æņØä ļīĆņāüņ£╝ļĪ£ ĒĢ┤ņłśļ®┤ ļ│Ćņ£äņÖĆ ņ£ĀņåŹņØä Fourier ĻĖēņłśļĪ£ ņĀäĻ░£ĒĢśņŚ¼ ņŖżĒÄÖĒŖĖļ¤╝ Ēīīļ×æ ļ¬©ĒśĢņØä ņĀ£ņŗ£ĒĢśņśĆļŗż. ņŖżĒÄÖĒŖĖļ¤╝ Ēīīļ×æ ļ¬©ĒśĢņØĆ ņŚ░ņĢłņŚŁņŚÉ Boussinesq ļ░®ņĀĢņŗØņØä ņ¦üņĀæ ņĀüņÜ®ĒĢśļŖö Ļ▓ĮņÜ░ ļČĆĻ│╝ļÉśļŖö ļ¦ÄņØĆ Ļ│äņé░ļ¤ēņ£╝ļĪ£ ņØĖĒĢ┤ ļ╣äĒÜ©ņ£©ņĀüņØ┤ļØ╝ļŖö ņĀÉņØä Ļ│ĀļĀżĒĢśļ®┤ ņĀüņĀłĒĢ£ ļīĆņĢłņ£╝ļĪ£ ņŚ¼Ļ▓©ņ¦äļŗż. ņØ┤ ņŚ░ĻĄ¼ņŚÉņä£ KirbyļŖö ņŖżĒÄÖĒŖĖļ¤╝ Ēīīļ×æļ¬©ĒśĢņØ┤ ĻĖ░ņĪ┤ņØś Ēżļ¼╝ĒśĢ ĻĘ╝ņé¼ņŗØļ│┤ļŗż Cnoidal Ēīīļ×æņŚÉ ņØśĒĢ£ ņ¦üļ”ĮņĀ£ņŚÉņä£ņØś ņŚ░Ēīī ņāØņä▒Ļ│╝ņĀĢņØä ņĀĢĒÖĢĒĢśĻ▓ī ĻĖ░ņłĀĒĢĀ ņłś ņ׳ņØīņØä Hammack, ScheffnerņÖĆ Segur (1989)ņØś ņŗżĒŚś ņ×ÉļŻīņÖĆņØś ļ╣äĻĄÉļź╝ ĒåĄĒĢ┤ ņ×ģņ”ØĒĢśņśĆņ£╝ļéś ņĖĪļ®┤ Ļ▓ĮĻ│äņĪ░Ļ▒┤ņŚÉ ņŻ╝ĻĖ░ņä▒ņØä ļČĆĻ│╝ĒĢ┤ņĢ╝ļ¦ī ĒĢśļŖö ļŗ©ņĀÉņØä ņ¦Ćļŗīļŗż.
ņØ┤ņ▓śļ¤╝ Ēśäņ×¼ ļ¼ĖĒŚīņŚÉņä£ ņ░ŠņĢäļ│╝ ņłś ņ׳ļŖö ņŚ░Ēīī Ļ┤ĆļĀ© ņŚ░ĻĄ¼ņØś ļīĆļČĆļČäņØĆ ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņ▓śļ¤╝ Ēīīļ×æņØś ņŚ¼ļ¤¼ ņä▒ņĀĢ ņżæ ņ¦äĒÅŁļ¦īņØä ļŗżļŻ©ļŖö ņŚÉļäłņ¦Ć Ļ│äņŚ┤ņØś Ēīīļ×æ ļ¬©ĒśĢņŚÉ ĻĖ░ņ┤łĒĢ£ ņłśņ╣śĒĢ┤ņäØņ£╝ļĪ£ ņŚ░Ēīīļź╝ ļŗżļŻ©ļ®░ ņ£äņāüļ│ä ņŚ░Ēīī ņāØņä▒Ļ│╝ņĀĢņØä ļŗżļŻ¼ ņŚ░ĻĄ¼ļŖö ņ░ŠĻĖ░Ļ░Ć ņēĮņ¦Ć ņĢŖļŗż. ĻĘĖļ¤¼ļéś ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņØś ņ£ĀļÅäĻ│╝ņĀĢņŚÉņä£ ĒÖ£ņÜ®ļÉśļŖö ņäŁļÅÖļ▓ĢņØä ņāüĻĖ░ĒĢśļ®┤ Ļ▒░ņ╣£ ĒĢ┤ņŚŁņŚÉņä£ ņĀäņłĀĒĢ£ ņŚ░ĻĄ¼ļŖö ļłäļØĮ ļÉ£ Ļ│Āņ░©ņä▒ļČäņ£╝ļĪ£ ņØĖĒĢ┤ ņśżļźśļź╝ ņ┤łļלĒĢĀ ņłś ņ׳ļŗż.
ņØ┤ņāüņØś ļģ╝ņØśļź╝ ĒåĀļīĆļĪ£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņŚ░Ēīī ņĀ£ņ¢┤ĒÜ©Ļ│╝ļź╝ OpenFoamĻĖ░ļ░ś Tool BoxņØĖ ihFoamņŚÉ ĻĖ░ņ┤łĒĢśņŚ¼ ņłśĒ¢ēļÉ£ ņłśņ╣śļ¬©ņØśļź╝ ĒåĄĒĢ┤ ņé┤ĒÄ┤ļ│┤ļĀż ĒĢ£ļŗż(Lara et al., 2011; Losada et al., 2008; Cho, 2019; Cho and Bae, 2019; Cho and Kang, 2017). ņØ┤ Ļ│╝ņĀĢņŚÉņä£ ņłśņ╣śļ░śņé¼ļŖö Ļ░£ļ░®Ļ▓ĮĻ│äņŚÉ ņŚÉļäłņ¦Ć ĒØĪņłśņĖĄ [Energy Absorbing Layer]ļź╝ Ļ▒░ņ╣śĒĢśņŚ¼ ņĄ£ņåīĒÖöĒĢśņśĆņ£╝ļ®░, ļ░®ĒīīņĀ£ ĻĖ░ņ┤łļź╝ ĻĄ¼ņä▒ĒĢśļŖö ņé¼ņäØņĖĄņŚÉņä£ņØś ņŚÉļäłņ¦Ć ņåīņé░ņØĆ del Jesus et al. (2012)ņØś VARANS [Volume Averaged Reynolds Averaged Navier Stokes Eq.] ļ¬©ĒśĢņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ĻĖ░ņłĀļÉ£ļŗż.
2ņןņŚÉņä£ļŖö ļģ╝ņØśļź╝ ņĀäĻ░£ĒĢśĻĖ░ ņ£äĒĢ┤ Schr├Čdinger ļ░®ņĀĢņŗØņŚÉ ĻĖ░ņ┤łĒĢ£ ņłśņ╣śļ¬©ņØśņÖĆ ņŚ░ĒīīņØś ņØ╝ļ░śņĀü ņä▒ņĀĢņØä ļŗżļŻ©ļ®░ 3ņןņŚÉņä£ļŖö ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉśļŖö ihFoam ņłśņ╣śļ¬©ĒśĢĻ│╝ VARANS ļ¬©ĒśĢņØä ņĀĢļ”¼ĒĢśņśĆļŗż. 4ņן, 5ņןņŚÉņä£ļŖö Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņŚ░ĒīīņĀ£ņ¢┤ ĒÜ©Ļ│╝ļź╝ ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ņłśĒ¢ēļÉ£ ņłśņ╣śļ¬©ņØśņÖĆ ņłśņ╣śĻ▓░Ļ│╝ļź╝ ņĀĢļ”¼ĒĢśņśĆļŗż. 5ņןņŚÉņä£ļŖö Ēśäņ×¼ Ļ░ĆņÜ®ĒĢ£ ļ░®ĒīīņĀ£ ņ¢æņŗØ ņżæ Ēīīļ×æ ņŚÉļäłņ¦Ć ņåīņé░ņØ┤ Ļ░Ćņן ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ĆļŖö ņé¼ņäØ Ļ▓Įņé¼ņŗØ ļ░®ĒīīņĀ£ņŚÉņä£ņØś ņŚ░Ēīī ĒŖ╣ņä▒ņØä Ļ░ĆļŖĀĒĢśĻĖ░ ņ£äĒĢ£ ņłśņ╣śļ¬©ņØśļÅä ĒĢ©Ļ╗ś ļŗżļŻ©ņŚłļŗż.
2. ņŚ░Ēīī ņłśļ”¼ĒŖ╣ņä▒ - Cubic Schr├Čdinger ļ░®ņĀĢņŗØņØä ņżæņŗ¼ņ£╝ļĪ£
ņŚ░ĒīīņØś ņØ╝ļ░śņĀü ņä▒ņĀĢņŚÉ Ļ┤ĆĒĢ┤ ņé┤ĒÄ┤ļ│┤ĻĖ░ ņ£äĒĢ┤ ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņØä ņłśņ╣śĒĢ┤ņäØ ĒĢśņśĆņ£╝ļ®░, ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĖ░ņłĀĒĢĀ ņłś ņ׳ļŗż.
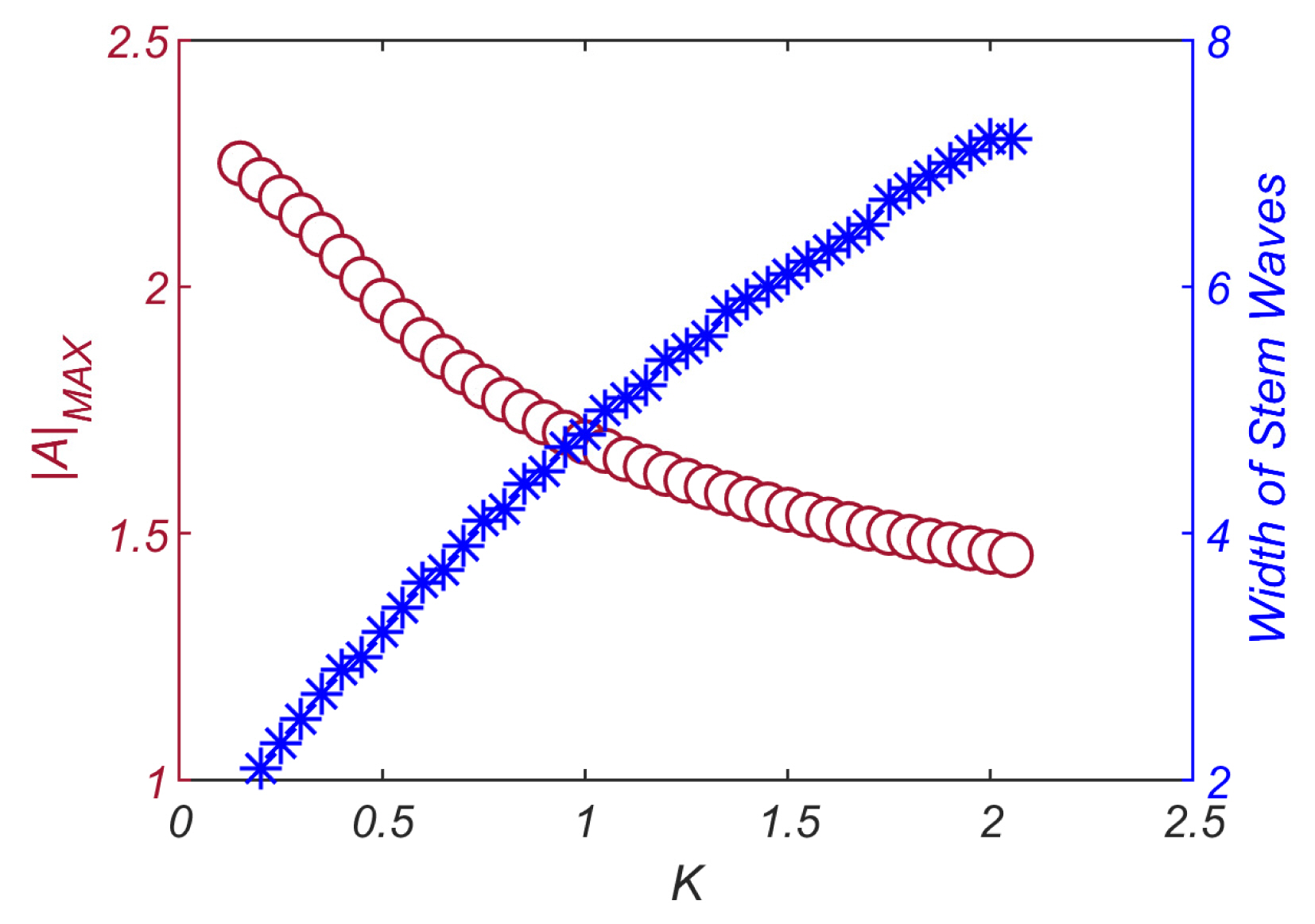
ņāüĻĖ░ ņŗØņŚÉņä£ KļŖö ņ×ģņé¼ Ēīīļ×æņØś ĒīīĒśĢ Ļ▓Įņé¼ņÖĆ ņ¦üļ”ĮņĀ£ņÖĆ ņ×ģņé¼ĒīīĻ░Ć ņØ┤ļŻ©ļŖö Ļ░üļÅä ╬Ą[Fig. 2 ņ░ĖņĪ░]ņŚÉ ļīĆĒĢ£ ņāüļīĆ ļ╣äņ£©, AļŖö ļ¼┤ņ░©ņøÉ ņ¦äĒÅŁ, XņÖĆ YļŖö ļ¼┤ņ░©ņøÉ ņóīĒæ£Ļ│äļź╝ ļéśĒāĆļé┤ļ®░ Ļ░üĻ░ü ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĖ░ņłĀļÉĀ ņłś ņ׳ļŗż.
Fig. 3ņŚÉļŖö ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ļÅäņŗ£ĒĢśņśĆļŗż. ĻĘĖļ”╝ņŚÉņä£ ņĢī ņłś ņ׳ļō» KĻ░Ć ņ╗żņ¦ÉņŚÉ ļö░ļØ╝ ņŚ░Ēīī ĒīīĻ│ĀļŖö Ļ░ÉņåīĒĢśļéś, ņŚ░ĒīīĻ░Ć ņāØņä▒ļÉśļŖö ņśüņŚŁņØś ĒÅŁņØĆ ņ”ØĻ░ĆĒĢśņśĆļŗż[Fig. 4 ņ░ĖņĪ░]. ņØ┤ļ¤¼ĒĢ£ Ļ▓ĮĒ¢źņØĆ Melville (1980), Mase (2002)ņØś ņŚ░ĻĄ¼ņŚÉņä£ļÅä ņ░ŠņĢäļ│╝ ņłś ņ׳ņ£╝ļ®░, ņ£Āņ×ģļÉśļŖö Ēīīļ×æ ņŚÉļäłņ¦ĆļŖö ņĀ£ĒĢ£ļÉśņ¦Ćļ¦ī ņ×ģņé¼ ĒīīĻ│ĀĻ░Ć ņ”ØĻ░ĆĒĢśļ®┤, ņØ┤ņŚÉ ļ╣äļĪĆĒĢśņŚ¼ ĒÖĢļīĆļÉśļŖö ņŚ░Ēīī ņāØņä▒ ĒÅŁĻ│╝ ĻĘĀĒśĢņØä ņØ┤ļŻ©ĻĖ░ ņ£äĒĢ£ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
3. ņłśņ╣śļ¬©ĒśĢ
ņłśņ╣śļ¬©ņØśļŖö OpenFoam ĻĖ░ļ░ś Tool boxņØĖ ihFoamņØä ņé¼ņÜ®ĒĢśņŚ¼ ņłśĒ¢ēļÉśļ®░, ihFoamņŚÉņä£ Ēīīļ×æļ¬©ĒśĢņØĆ RANS(Reynolds Averaged Navier-Stokes equation)ņÖĆ ņ¦łļ¤ē ļ│┤ņĪ┤ņŗØņ£╝ļĪ£ ĻĄ¼ņä▒ļÉśļ®░, ņ×Éņ£Ā ņłśļ®┤ņØĆ VOF(Volume Of Fraction) ļ▓ĢņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ņČöņĀüļÉ£ļŗż.
3.1 Ēīīļ×æļ¬©ĒśĢ
ihFoamņŚÉņä£ ņ░©ņÜ®ĒĢśļŖö Ēīīļ×æļ¬©ĒśĢņØĖ RANS, ņ¦łļ¤ē ļ│┤ņĪ┤ņŗØ, VOFņŗØņØä ĻĖ░ņłĀĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░Öņ£╝ļ®░
ņŚ¼ĻĖ░ņä£ UļŖö ņåŹļÅä ļ▓ĪĒä░, gļŖö ņżæļĀźĻ░ĆņåŹļÅä, ŽüļŖö ļ░ĆļÅä, ╬╝eff = ╬╝+ŽüvturbļŖö ļÅÖņĀÉņä▒Ļ│äņłś, p*ļŖö ņ£Āņé¼ ļÅÖņĀüņĢĢļĀź, XļŖö ņ£äņ╣śļ▓ĪĒä░, ╬▒1ļŖö Ļ░üĻ░üņØś ļŗ©ņ£äĻ▓®ņ×ÉņŚÉņä£ ĒĢ┤ņłśĻ░Ć ņĀÉņ£ĀĒĢśĻ│Ā ņ׳ļŖö ņ▓┤ņĀüņØä ņØśļ»ĖĒĢśļŖö VOF Ļ│äņłśļź╝ Ļ░üĻ░ü ļéśĒāĆļéĖļŗż.
3.2 Porous mediaņŚÉņä£ņØś Ēīīļ×æļ¬©ĒśĢ
Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ĻĖ░ņ┤łļŖö ņé¼ņäØ ņĖĄņ£╝ļĪ£ ĻĄ¼ņä▒ļÉśļ®░, ņØ┤ Ļ▓ĮņÜ░ ļŗżĻ│Ąņä▒ ļ¦żņ¦łņŚÉņä£ ļ░£ņāØĒĢśļŖö ĒśĢņāüĒĢŁļĀźĻ│╝ Ļ┤Ćņä▒ ĒĢŁļĀźņ£╝ļĪ£ ņØĖĒĢ┤ Ēīīļ×æ ļ¬©ĒśĢņØĆ ņłśņĀĢļÉśņ¢┤ņĢ╝ ĒĢ£ļŗż.
Darcy(1856)ņØś ņé¼ņ¦łĒåĀ ļé┤ļČĆņŚÉņä£ņØś ņ£Āņ▓┤ ĒØÉļ”äņŚÉ Ļ┤ĆĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ņĢīļĀżņ¦ä Ēøä, ļŗżĻ│Ąņä▒ ļ¦żņ¦łņŚÉņä£ņØś ņ£Āņ▓┤ ĒĢ┤ņäØņØä ĒśĢņāüĒĢŁļĀźņ£╝ļĪ£ ĻĖ░ņłĀĒĢśļĀżļŖö ĒØÉļ”äņØĆ ņØ┤Ēøä ļŗżĻ│Ąņä▒ ļ¦żņ¦łņŚÉņä£ņØś ņ£ĀļÅÖ ĒĢ┤ņäØņŚÉ Ēü░ ĒØÉļ”äņØä ĒśĢņä▒ĒĢ£ļŗż. ņĖĄļźśņØś Ļ▓ĮņÜ░ ņäĀĒśĢ ĒśĢņāüĒĢŁļĀźļ¦īņ£╝ļĪ£ļÅä ĒĢ┤ņäØĒĢĀ ņłś ņ׳ņ£╝ļéś, Forcheimer(1901)ļŖö Ēü░ Reynolds ņłśņŚÉņä£ļÅä ņĀüņÜ®ĒĢĀ ņłś ņ׳ļÅäļĪØ ņØ┤ņ░© ĒśĢņāü ĒĢŁļĀź ĒĢŁņØä ņČöĻ░ĆĒĢśņśĆņ£╝ļ®░, Polubarinova-Kochina(1962)ļŖö 1901ļģäņŚÉ ForcheimerĻ░Ć ņĀ£ņŗ£ĒĢ£ ņŗØņØä ļ╣äņĀĢņāüļźśļĪ£ ĒÖĢņןĒĢśĻĖ░ ņ£äĒĢ┤ Ļ┤Ćņä▒ļĀźņØä ņČöĻ░ĆĒĢśņśĆļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö del Jesus et al.(2012)ņŚÉ ņØśĒĢ┤ ņĀ£ņŗ£ļÉ£ VARANSļź╝ ņé¼ņÜ®ĒĢśņśĆņ£╝ļ®░ ņØ┤ļź╝ ĻĖ░ņłĀĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņāüĻĖ░ ņŗØņŚÉņä£ uļŖö ĒÅēĻĘĀņ£ĀņåŹ ļśÉļŖö DarcyņåŹļÅä, nņØĆ Ļ│ĄĻĘ╣ļźĀ, AņÖĆ BļŖö ĒśĢņāüĒĢŁļĀź Ļ│äņłś, cļŖö Ļ┤Ćņä▒ļĀź ĒśĢņāüĒĢŁļĀź Ļ│äņłśļĪ£ ļ¼╝ņä▒ņŚÉ ņóģņåŹĒĢ£ļŗż.
ļŗżĻ│Ąņä▒ ļ¦żņ¦łņŚÉņä£ ļ╣äņ¢┤ņ׳ļŖö Ļ│ĄĻ░äņŚÉ ņĪ┤ņ×¼ĒĢśļŖö ņ£Āņ▓┤ņØś ņåŹļÅäļź╝ ņØśļ»ĖĒĢśļŖö ņŗżņĀ£ ņåŹļÅäļŖö ĒÅēĻĘĀņ£ĀņåŹ ļśÉļŖö Darcy ņåŹļÅäļź╝ ļéśĒāĆļé┤ļŖö uņÖĆ ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ļ┤ĆĻ│äņŗØņØä ņČ®ņĪ▒ĒĢ£ļŗż.
ņäĀĒśĢ ĒśĢņāüĒĢŁļĀź Ļ│äņłś A, ļ╣äņäĀĒśĢ ĒśĢņāüĒĢŁļĀź Ļ│äņłś BļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņĀĢņØśļÉśļ®░(Cho and Kang, 2017),
ņŚ¼ĻĖ░ņä£ D50ņØĆ ļŗżĻ│Ąņä▒ ļ¼╝ņ¦łņØś ņżæņĢÖ ņ¦üĻ▓Į, KCļŖö Keulegan-Carpenterņłśļź╝ Ļ░üĻ░ü ļéśĒāĆļé┤ļ®░ KCļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĖ░ņłĀļÉĀ ņłś ņ׳ļŗż.
ņŗØ (12)ņŚÉņä£ uMņØĆ ņĄ£ļīĆ ņ¦äļÅÖ ņåŹļÅä, ToļŖö ņ¦äļÅÖņŻ╝ĻĖ░ļź╝ ļéśĒāĆļé┤ļ®░, KCļŖö vortex induced vibrationņ£╝ļĪ£ ņØĖĒĢ£ ņČöĻ░ĆņĀüņØĖ ļ¦łņ░░ņØä Ļ│ĀļĀżĒĢśĻĖ░ ņ£äĒĢ┤ ļÅäņ×ģļÉśņŚłļŗż. ļ¦łņ░░ ļ¦żĻ░£ļ│ĆņłśļōżĻ│╝ ņŚ░Ļ┤ĆļÉśņ¢┤ ╬▒ņÖĆ ╬▓ļŖö ņĪ░ņĀĢļÉśļ®░, Ļ┤Ćņä▒ļĀź Ļ│äņłś cĻ░ÆņØĆ 0.34ļĪ£ ņ£Āņ¦ĆļÉ£ļŗż.
4. ņłśņ╣śļ¬©ņØś
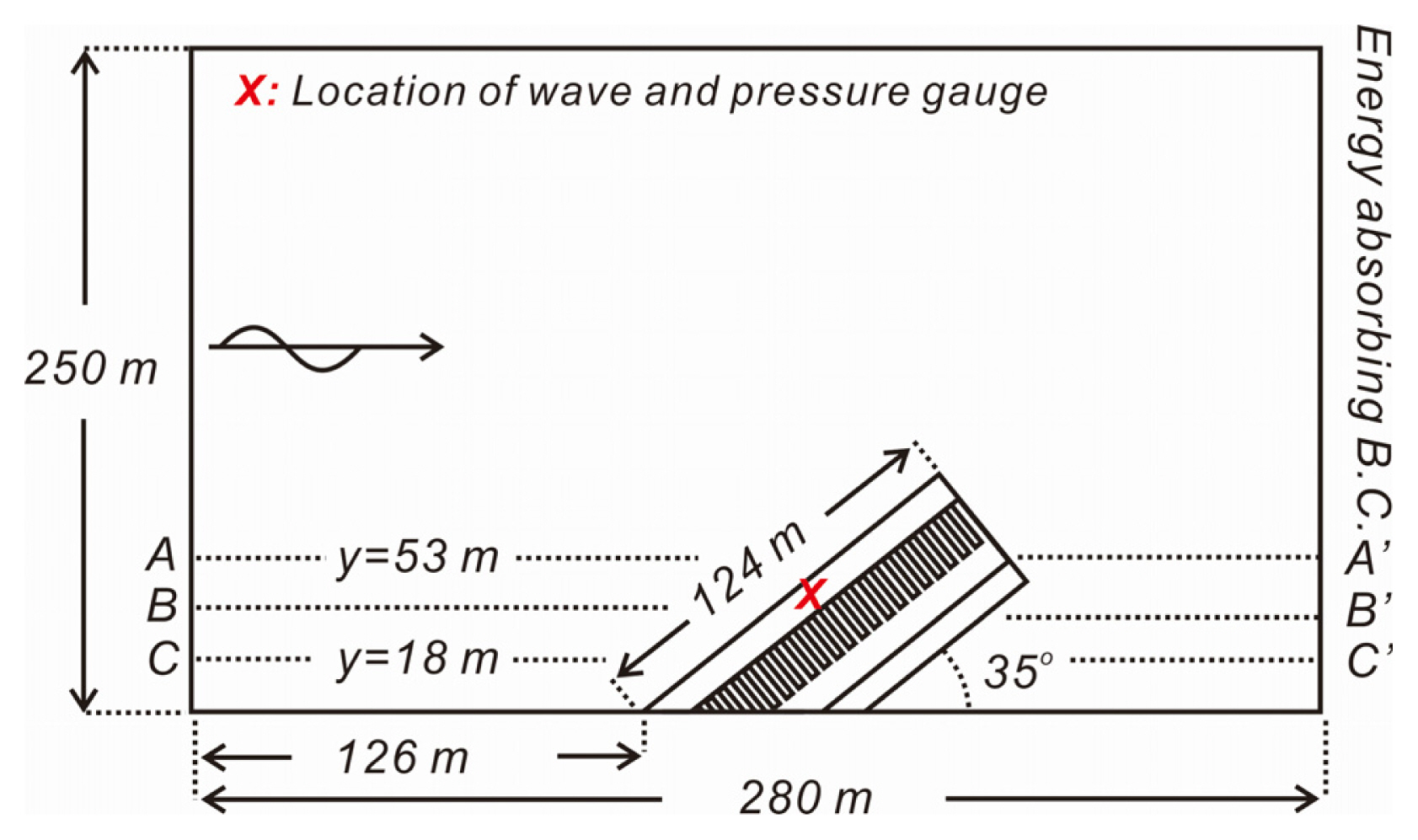
ļīĆņłśņŗ¼ ĒĢ┤ņŚŁņŚÉņä£ ņäĀĒśĖļÉśļŖö Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņŚ░ĒīīņĀ£ņ¢┤ ĒÜ©Ļ│╝ļź╝ ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ņłśņ╣śļ¬©ņØśļź╝ ņłśĒ¢ēĒĢśņśĆņ£╝ļ®░, ļ╣äĻĄÉļź╝ ņ£äĒĢ┤ ņ¦üļ”Į ļ░®ĒīīņĀ£ļź╝ ļīĆņāüņ£╝ļĪ£ ĒĢ£ ņłśņ╣śļ¬©ņØśļÅä ĒĢ©Ļ╗ś ņłśĒ¢ēĒĢśņśĆļŗż[Fig. 5 ņ░ĖņĪ░]. Fig. 6ņŚÉ ļÅäņŗ£ĒĢ£ Ļ│äņé░ ņśüņŚŁņØĆ 350 ├Ś 250 ├Ś 40 = 3,500,000Ļ░£ņØś ņĀłņĀÉņ£╝ļĪ£ ņØ┤ņé░ĒÖöĒĢśņśĆņ£╝ļ®░, Table 1ņŚÉļŖö ņłśņ╣śļ¬©ņØśņŚÉ ņé¼ņÜ®ļÉ£ Ēīīļ×æ ņĀ£ņøÉņØä ņĀĢļ”¼ĒĢśņśĆļŗż.
ļ░®ĒīīņĀ£ ĻĖ░ņ┤łļŖö ņ¦üĻ▓Į D50 = 3 cmņØĖ ņé¼ņäØņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆņ£╝ļ®░. Ēł¼ņłśņĖĄņŚÉņä£ņØś ņ£ĀļÅÖņØĆ Navier Stokes Eq.ņŚÉ ņČöĻ░Ć ĒĢŁļĀźņØä ļÅäņ×ģĒĢśņŚ¼ ĒĢ┤ņäØĒĢśņśĆļŗż. ņ×ģņé¼ĒīīĻ│Ā, ņŻ╝ĻĖ░, ņłśņŗ¼ņØĆ Ļ░üĻ░ü H=3.5, 5, 6.5m, T=10ņ┤ł, h=26.25m, ĒīīĒśĢņØĆ ņŚ░Ēīī ņāØņä▒ Ļ░ĆļŖźņä▒ņØä ļåÆņØ┤ĻĖ░ ņ£äĒĢ┤ Korteweg-de VriesņŗØņØś ĒĢ┤ņäØĒĢ┤ļĪ£ ņĀĢņØśļÉśļŖö Cnoidal waveļĪ£ ņĘ©ĒĢśņśĆņ£╝ļ®░, Cnoidal waveļź╝ ĻĖ░ņłĀĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ ╬ČļŖö ĒĢ┤ņłśļ®┤ ļ│Ćņ£ä, HļŖö ĒīīĻ│Ā, CnņØĆ Jacobi elliptic function, cļŖö ĒīīņåŹ, LņØĆ Ēīīņן, TļŖö ņŻ╝ĻĖ░, mņØĆ 0Ļ│╝ 1ņé¼ņØ┤ņØś Ļ░ÆņØä ņ¦ĆļŗłļŖö elliptic parameterļź╝ Ļ░üĻ░ü ļéśĒāĆļéĖļŗż. KmņØĆ ņĀ£1ņóģ ĒāĆņøÉņĀüļČä, EmņØĆ ņĀ£2ņóģ ĒāĆņøÉņĀüļČäņØä Ļ░üĻ░ü ļéśĒāĆļé┤ļ®░, KmĻ│╝ EmņØĆ mĻ░ÆņŚÉ ņóģņåŹĒĢ£ļŗż. Cnoidal wave ĒīīĒśĢņØĆ mņØ┤ 0ņŚÉ ņłśļĀ┤ĒĢśļ®┤ StokesŌģĀĒīīĒśĢņŚÉ, mņØ┤ 1ņŚÉ ņłśļĀ┤ĒĢśļ®┤ solitary wave ĒīīĒśĢņŚÉ ņłśļĀ┤ĒĢśļ®░, Cnoidal wave ņŚÉņä£ņØś ņ£ĀņåŹņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĖ░ņłĀļÉĀ ņłś ņ׳ļŗż.
5. ņłśņ╣śĻ▓░Ļ│╝
5.1 Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņŚ░Ēīī ņĀ£ņ¢┤ĒÜ©Ļ│╝
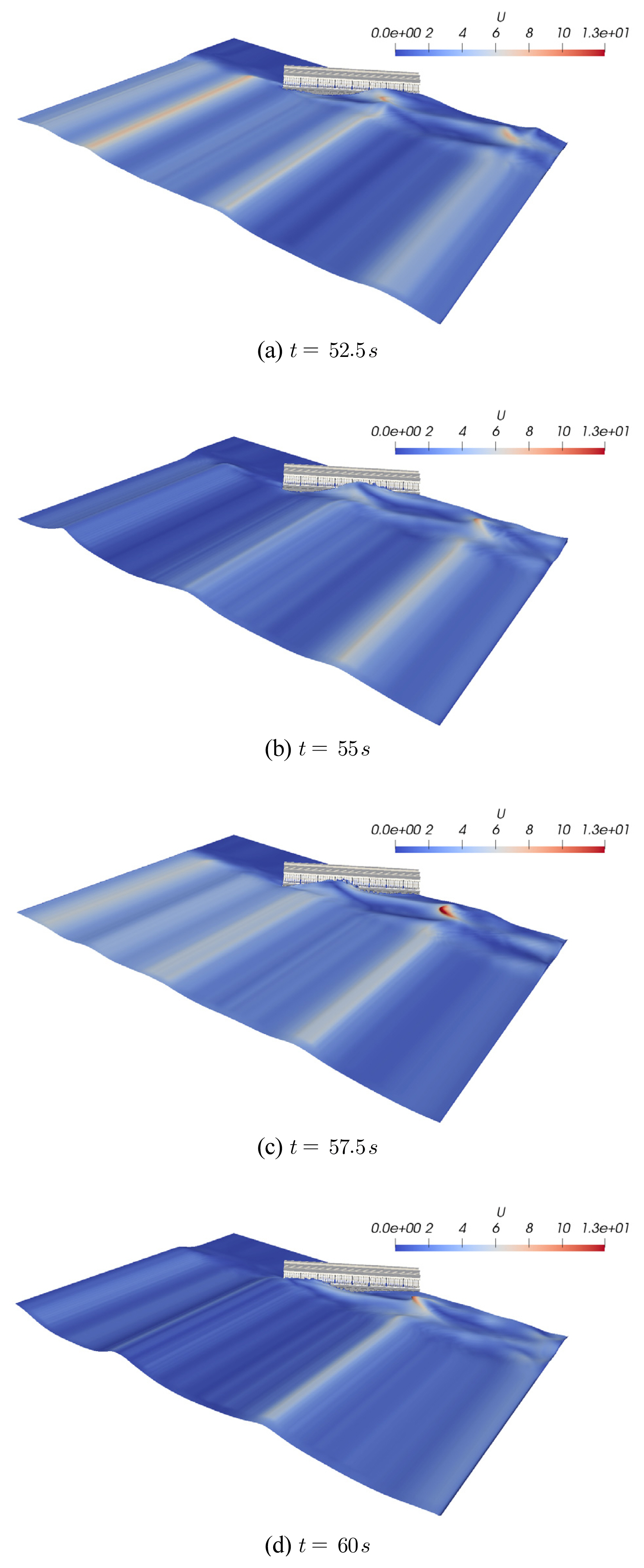
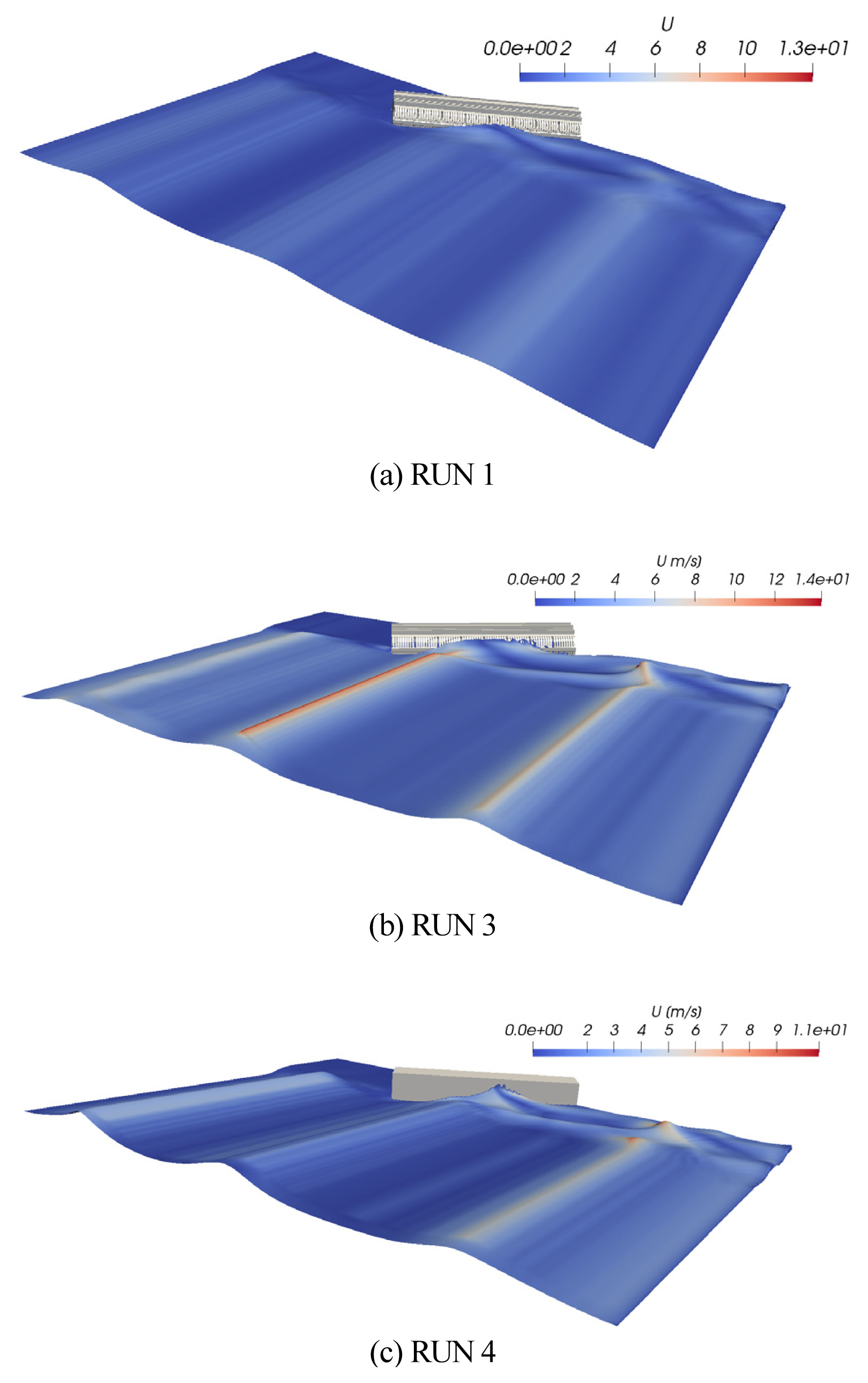
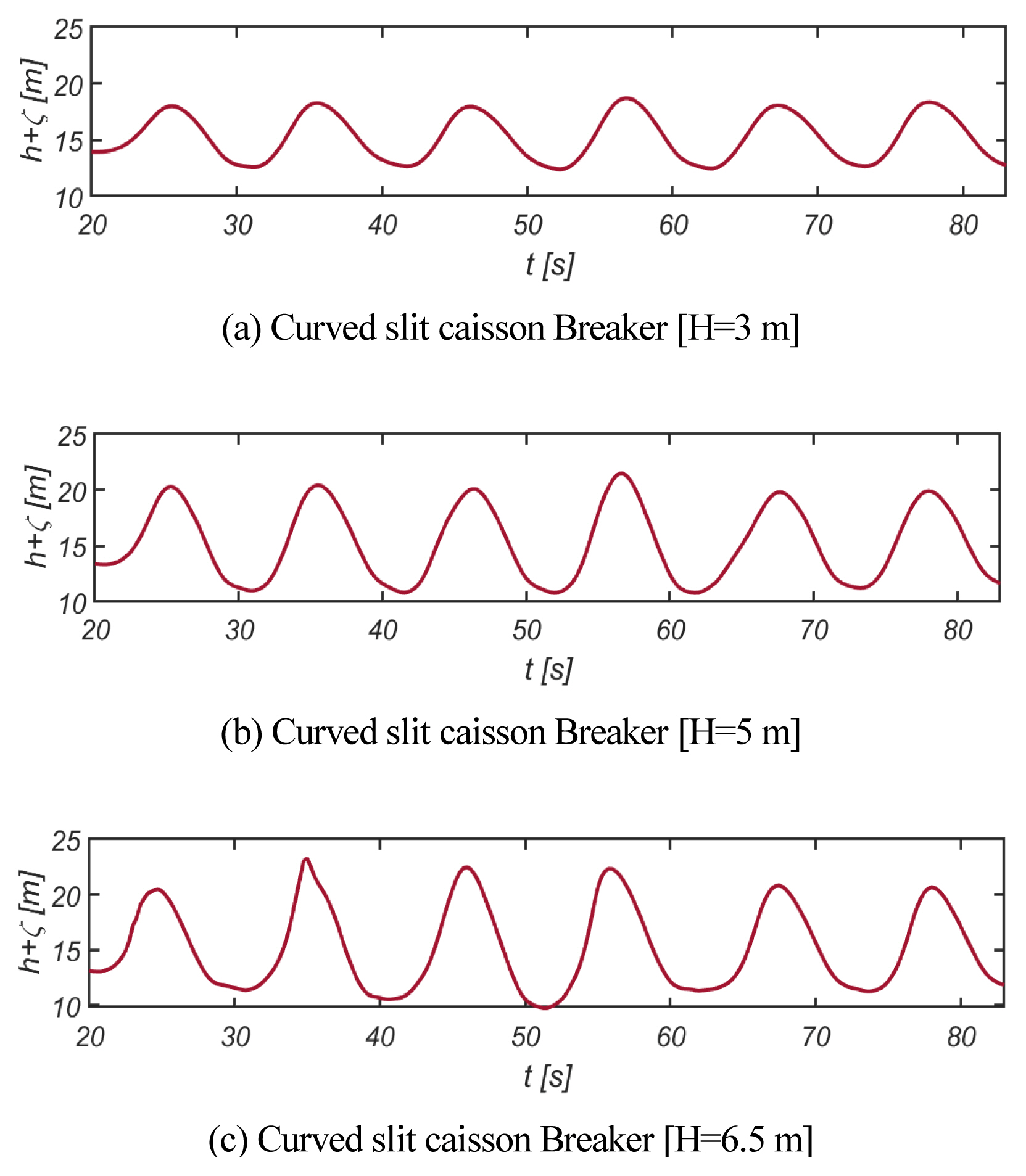
Fig. 7ņŚÉļŖö RUN 2ņŚÉņä£ Ļ┤ĆņĖĪļÉ£ ņ×Éņ£Āņłśļ®┤ snapshotņØä ņł£ņ░©ņĀüņ£╝ļĪ£ ņĀĢļ”¼ĒĢśņśĆļŗż. ņŚ░ĒīīĻ░Ć ņāØņä▒ļÉśņ¢┤ ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēļÉśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ņ×ģņé¼ ĒīīĻ│ĀĻ░Ć ņŚ░Ēīī Ēü¼ĻĖ░ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ Fig. 8ņŚÉļŖö RUN 1, 3, 4ņŚÉņä£ ņŚ░Ēīī ĒīīĻ│ĀĻ░Ć ņĀĢņĀÉņŚÉ ņØ┤ļźĖ ņł£Ļ░äņŚÉņä£ņØś ņ×Éņ£Āņłśļ®┤ snapshotņØä ņĀĢļ”¼ĒĢśņśĆļŗż. ņēĮĻ▓ī ņśłņāüĒĢ┤ ļ│╝ ņłś ņ׳ļō»ņØ┤ ļŗ©ņł£ ņ¦üļ”ĮņĀ£ņŚÉņä£ Ļ░Ćņן Ļ▒░ņ╣£ ņŚ░ĒīīĻ░Ć ņāØņä▒ļÉśļ®░[Fig. 8(c) ņ░ĖņĪ░], ņ×ģņé¼ ĒīīĻ│ĀĻ░Ć Ļ░Ćņן ņ×æņØĆ RUN 1ņŚÉņä£ ņŚ░Ēīī ĒīīĻ│ĀĻ░Ć Ļ░Ćņן ņ×æņØĆ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż [Fig. 9 ņ░ĖņĪ░].
ļśÉĒĢ£ ņ£ĀņłśņŗżņŚÉņä£ ņ¦äĒ¢ēļÉśļŖö ņŚÉļäłņ¦Ć ņåīņé░Ļ│╝ ņØ┤ļĪ£ ņØĖĒĢ£ ļ░śņé¼ņ£© Ļ░ÉņåīļĪ£ ļ░®ĒīīņĀ£ ņĀäļ®┤ĒĢ┤ņŚŁņŚÉņä£ Ļ┤ĆņĖĪļÉśļŖö ņĀĢņāüĒīīļÅÖĻ│äļŖö ņ¦üļ”ĮņŗØ ļ░®ĒīīņĀ£ņØś Ļ▓ĮņÜ░ļ│┤ļŗż ļŹ£ ļ¬ģņ¦ĢĒĢśļŗż[Fig.7, 8 ņ░ĖņĪ░].
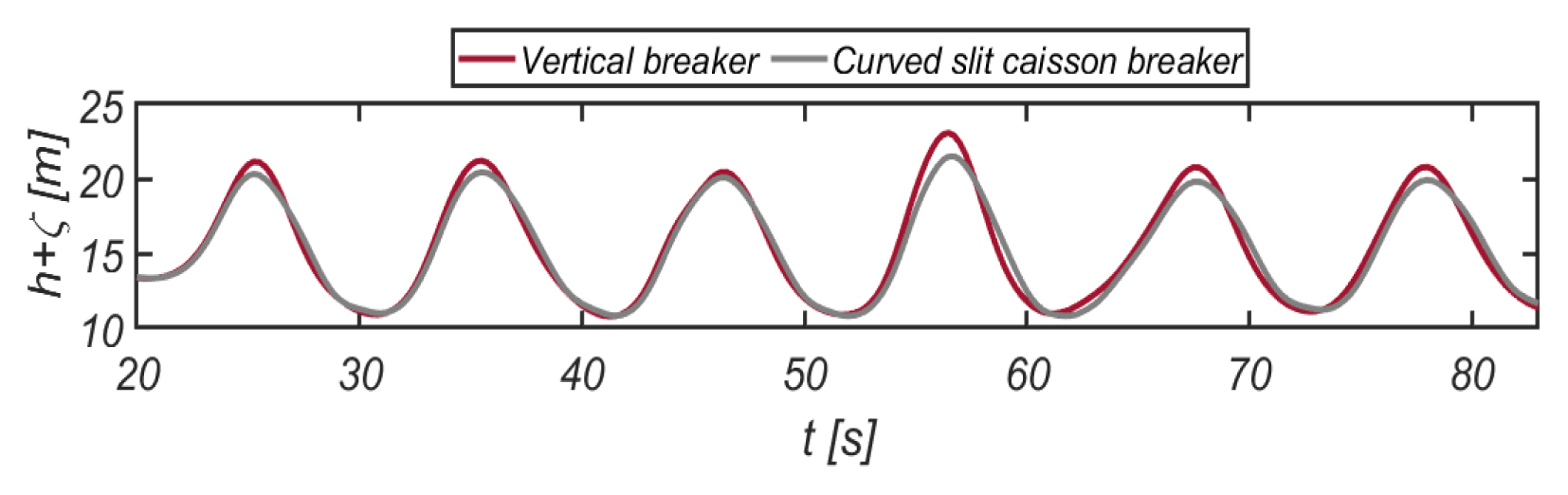
Fig. 10ņŚÉļŖö ļ░®ĒīīņĀ£ ņ¢æņŗØņØ┤ ņŚ░ĒīīņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ RUN 2, 4ņŚÉņä£ ļ░®ĒīīņĀ£ ņĀäļ®┤ĒĢ┤ņŚŁņŚÉ Ļ▒░ņ╣śļÉ£ Wave Gauge [Fig. 6 ņ░ĖņĪ░]ņŚÉņä£ Ļ┤ĆņĖĪļÉ£ ņ×Éņ£Āņłśļ®┤ ļ│Ćņ£ä ņŗ£Ļ│äņŚ┤ņ×ÉļŻīļź╝ ļ╣äĻĄÉĒĢśņśĆļŗż. Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś Ļ▓ĮņÜ░ ĒīīĻ│ĀĻ░Ć ņĄ£ļīĆ 2mĻ╣īņ¦Ć, ņżäņ¢┤ļō£ļŖö Ļ▓āņ£╝ļĪ£ ļ¬©ņØś ļÉśņ¢┤ Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ļŖö ņŚ░ĒīīņĀ£ņ¢┤ ĒÜ©Ļ│╝ļź╝ ņ¦ĆļŗłļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
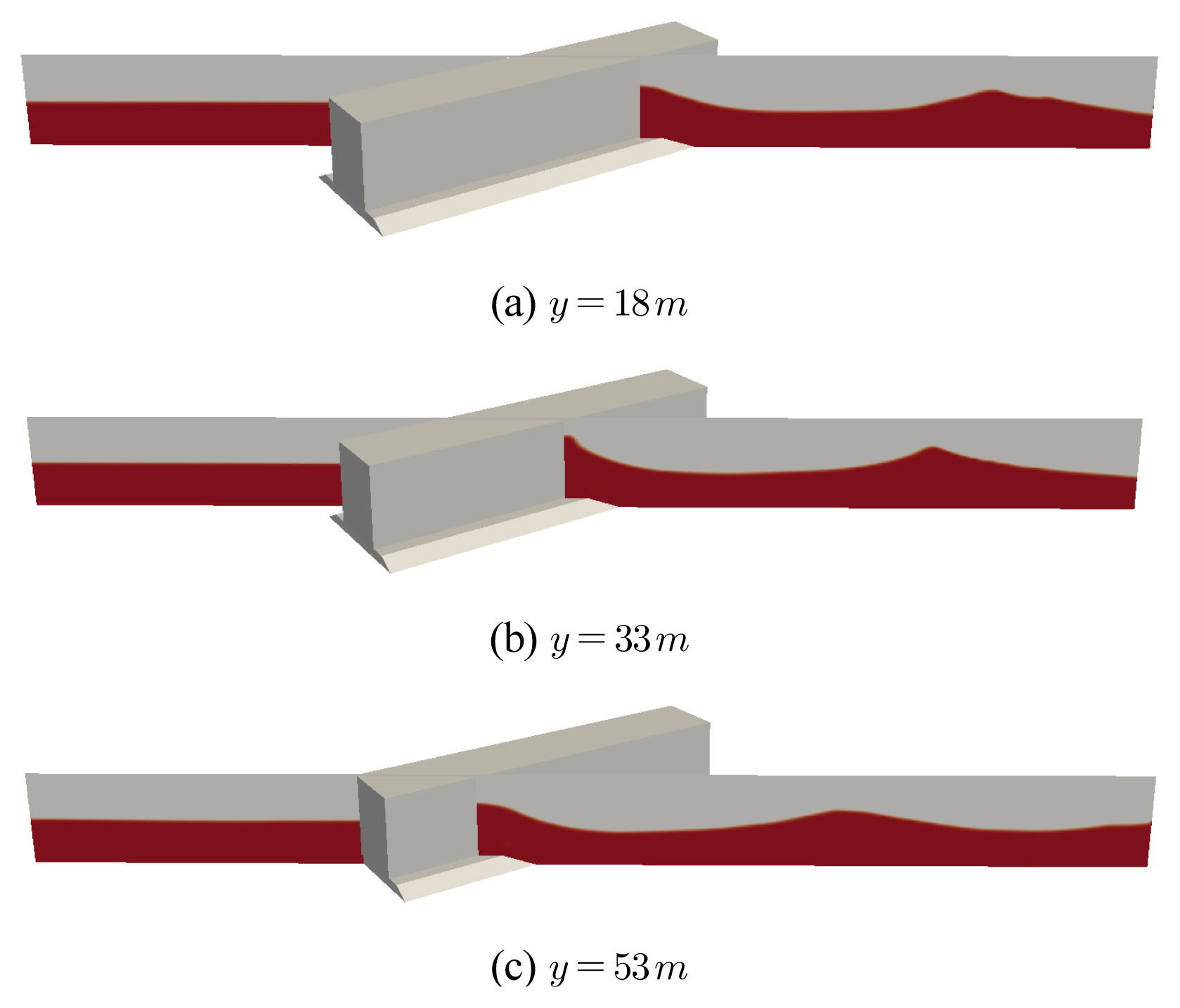
Fig. 11ņŚÉļŖö ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēļÉśļŖö ņŚ░Ēīīļź╝ ļŹöņÜ▒ ļ¬ģņ¦ĢĒĢśĻ▓ī ļō£ļ¤¼ļé┤ĻĖ░ ņ£äĒĢ┤ ļ░®ĒīīņĀ£ļź╝ Ļ░ĆļĪ£ņ¦Ćļź┤ļŖö ļŗ©ļ®┤ A-AŌĆ▓, B-BŌĆ▓, C-CŌĆ▓ņŚÉņä£ņØś ņŚ░ĒīīĻ░Ć ņĀĢņĀÉņŚÉ ņØ┤ļźĖ ņł£Ļ░äņŚÉņä£ņØś ņ×Éņ£Āņłśļ®┤ snapshotņØä ņĀĢļ”¼ĒĢśņśĆļŗż. ņŚ░ĒīīĻ░Ć ņ¦äĒ¢ēļÉśļ®░ ņŚ░Ēīī ĒīīĻ│ĀļŖö Ļ░ÉņåīĒĢśļéś ĻĘ£ļ¬©ļŖö ņ”ØĻ░ĆĒĢśļŖö ņŚ░ĒīīņØś ņä▒ņĀĢņØ┤ ņĀĢĒÖĢĒ׳ ļ¬©ņØś ļÉśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż[Fig. 12 ņ░ĖņĪ░].
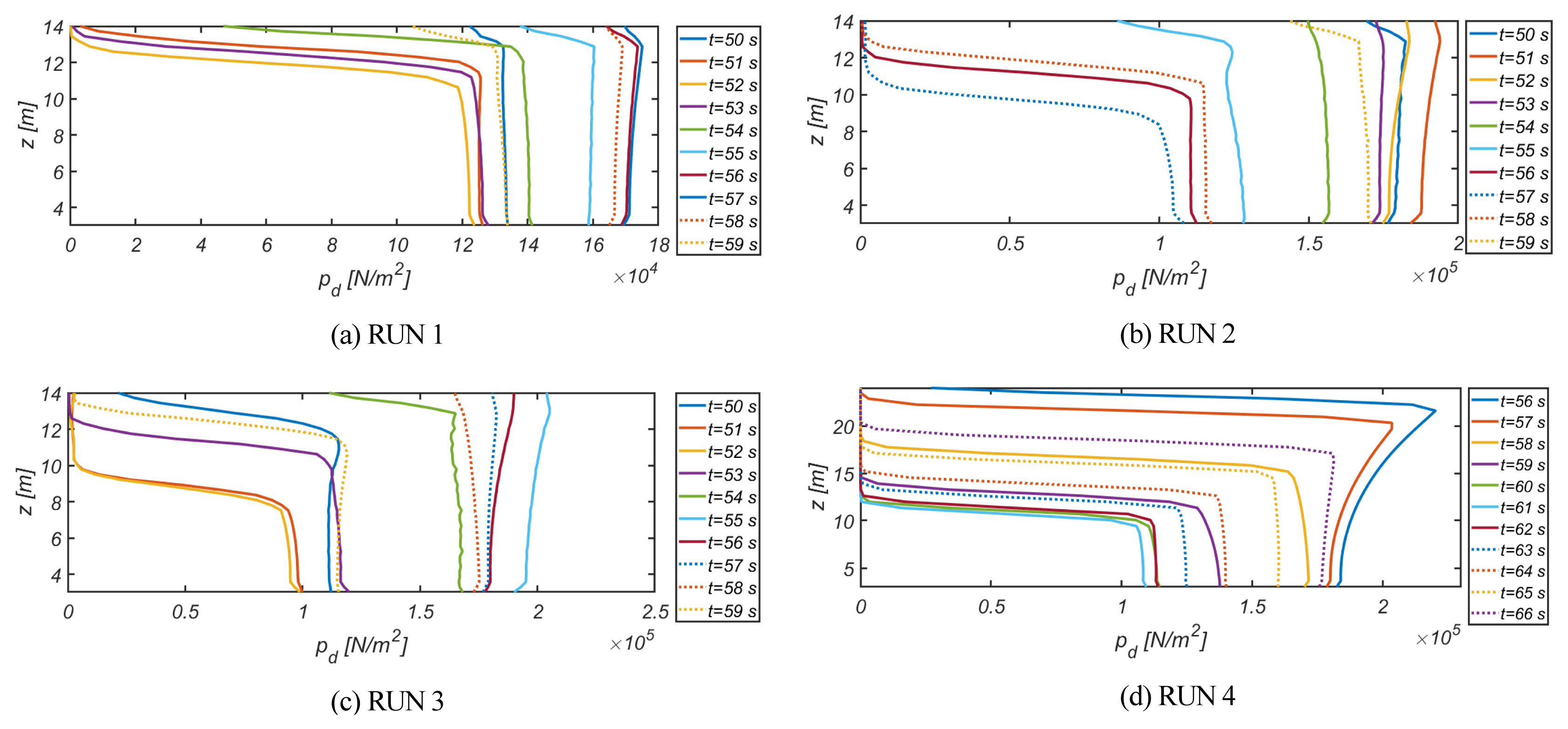
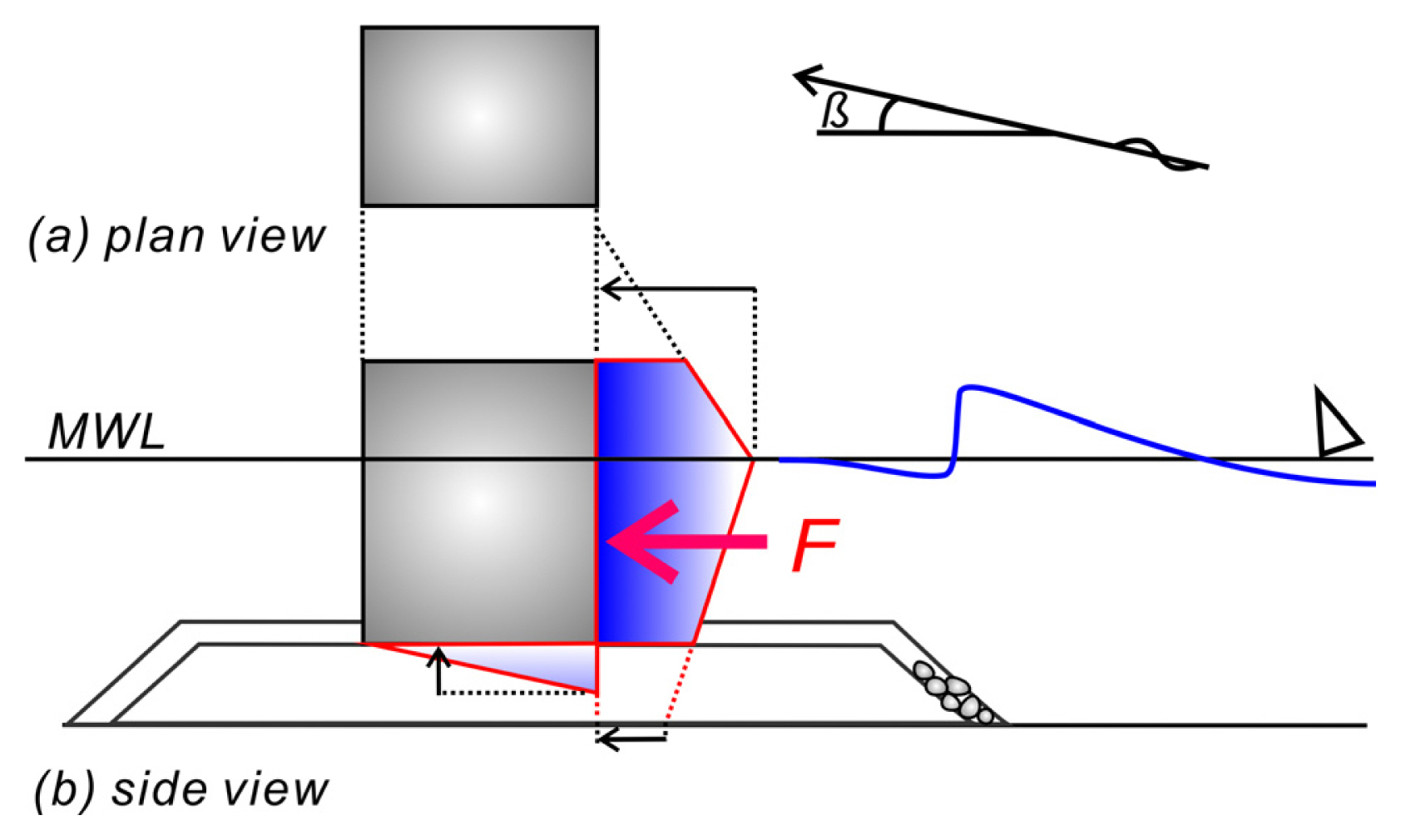
Fig. 13, 14ņŚÉļŖö ļ░®ĒīīņĀ£ ņĀäļ®┤ĒĢ┤ņŚŁņŚÉ Ļ▒░ņ╣śļÉ£ wave gauge [Fig. 6 ņ░ĖņĪ░]ņŚÉņä£ Ļ┤ĆņĖĪļÉ£ ņČ®Ļ▓® ņćäĒīīņĢĢ[impulsive hydrodynamic force]ņØ┤ ĒĢśļéśņØś ļŗ©ņ£ä ņŻ╝ĻĖ░ņŚÉ Ļ▒Ėņ│É ļ│ĆĒÖöĒĢśļŖö ņ¢æņāüņØä ņĀĢļ”¼ĒĢśņśĆļŗż. ņ£äņāüļ│ä ļ│ĆĒÖöļź╝ ļ¬©ļæÉ ļŗ┤ņĢäļé┤ĻĖ░ ņ£äĒĢ┤ ĒĢśļéśņØś ļŗ©ņ£ä ņŻ╝ĻĖ░ļŖö ļ¬©ļæÉ ņŚ┤ Ļ░£ņØś frameņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆļŗż. Goda(1985)Ļ░Ć ņØ┤ņĢ╝ĻĖ░ĒĢśļŖö ņé¼ļŗżļ”¼Ļ╝┤ ļČäĒżļź╝ ĒÖĢņØĖĒĢĀ ņłś ņ׳ņ£╝ļ®░[Fig. 15 ņ░ĖņĪ░], Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ©ņØś Ļ▓ĮņÜ░ņŚÉņä£ ļŗ©ņł£ ņ¦üļ”ĮņĀ£ ļ│┤ļŗż ņČ®Ļ▓® ņćäĒīīņĢĢņØ┤ 15% ļé┤ņÖĖļĪ£ Ļ▓ĮĻ░ÉļÉśļŖö Ļ▓āņØä ņĢī ņłś ņ׳ņ×É. ņØ┤ļ¤¼ĒĢ£ ĒśäņāüņØĆ Ļ│Īļ®┤ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ©ņØś Ļ░£ĻĄ¼ļČĆļĪ£ Ēł¼Ļ│╝ļÉśļŖö ņ£ĀļÅÖņ£╝ļĪ£ ņØĖĒĢ┤ ņÜ┤ļÅÖļ¤ē ņØ┤ņåĪļźĀņØ┤ ļČäņé░ļÉśņ¢┤ ļ░£ņāØĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż. Fig. 16ņŚÉļŖö ņŚ░Ēīī ņāØņä▒ņŗ£ ņ£ĀņåŹ ļ▓ĪĒä░ļÅäļź╝ ņ░©ļĪĆļīĆļĪ£ ļÅäņŗ£ĒĢśņśĆļŗż. Ļ│Īļ®┤ ņŖ¼ļ”┐ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēļÉśļŖö ņŚ░ĒīīņØś ņä▒ņĀĢņØ┤ ņל ļō£ļ¤¼ļé£ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
5.2 ņé¼ņäØņŗØ ļ░®ĒīīņĀ£ņŚÉņä£ņØś ņŚ░Ēīī ĒŖ╣ņä▒
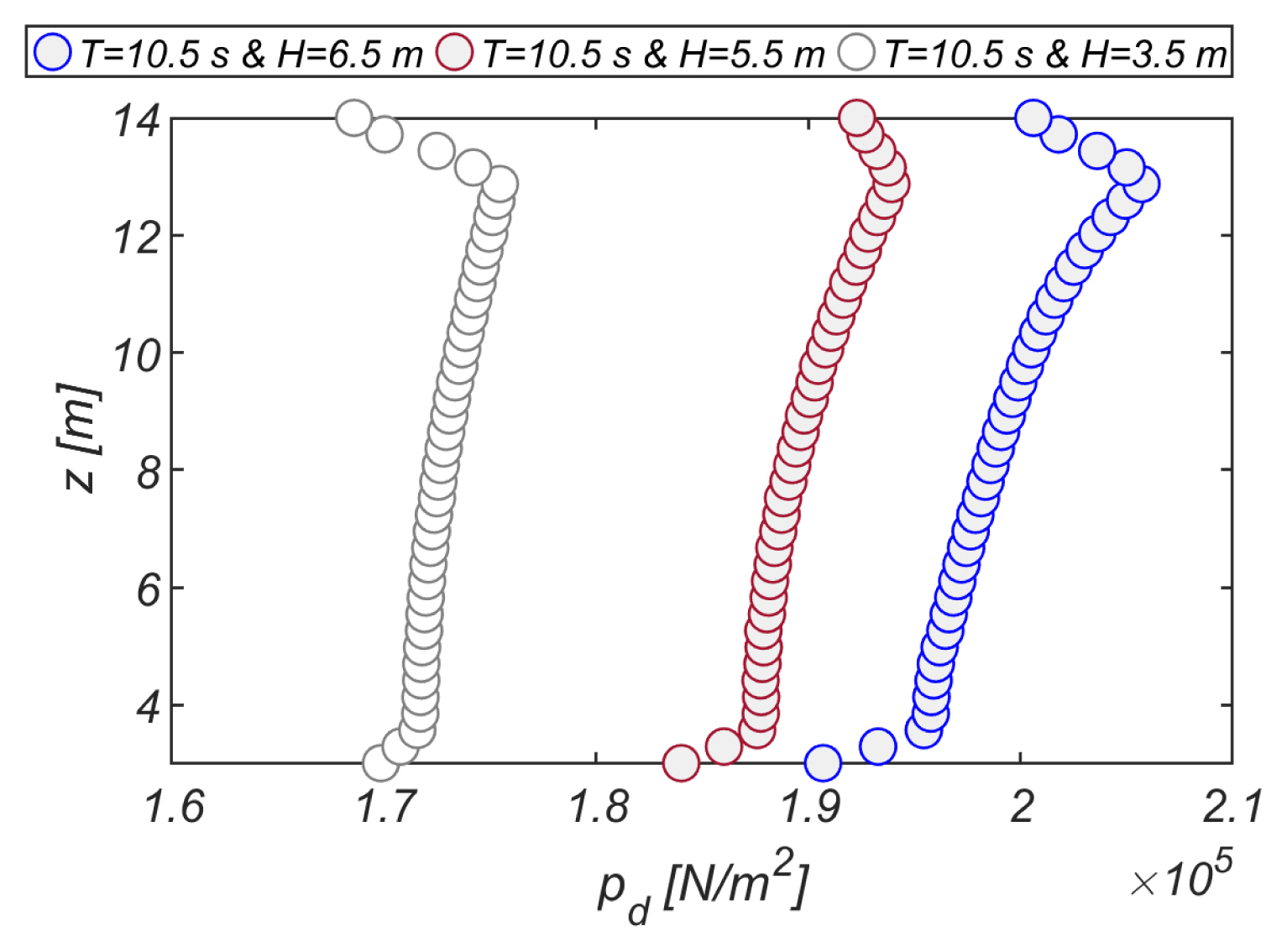
1ņןņŚÉņä£ ļŗżļŻ©ņŚłļō» ļé┤ņŖĄĒĢśļŖö Ēīīļ×æ ņŚÉļäłņ¦ĆņØś ņåīņé░ņØĆ ņé¼ņäØ Ļ▓Įņé¼ņŗØ ļ░®ĒīīņĀ£ņŚÉņä£ Ļ░Ćņן ĒÜ©ņ£©ņĀüņ£╝ļĪ£ Ļ░ĢņĀ£ļÉ£ļŗż. ļ│Ė ņĀłņŚÉņä£ļŖö ņé¼ņäØ Ļ▓Įņé¼ņŗØ ļ░®ĒīīņĀ£ņŚÉņä£ Ļ░ĢņĀ£ĒĢśļŖö Ēīīļ×æ ņŚÉļäłņ¦Ć ņåīņé░ņØ┤ ņŚ░ĒīīņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ņé┤ĒÄ┤ļ│┤ĻĖ░ ņ£äĒĢ┤ Ēś╝ņä▒ļ░®ĒīīņĀ£ņŚÉ ļ╣äņŖżļō¼Ē׳ ņ×ģņé¼ĒĢśļŖö Ēīīļ×æņØś ņĀäĒīīĻ│╝ņĀĢņØä ņłśņ╣śļ¬©ņØś ĒĢśņśĆļŗż.
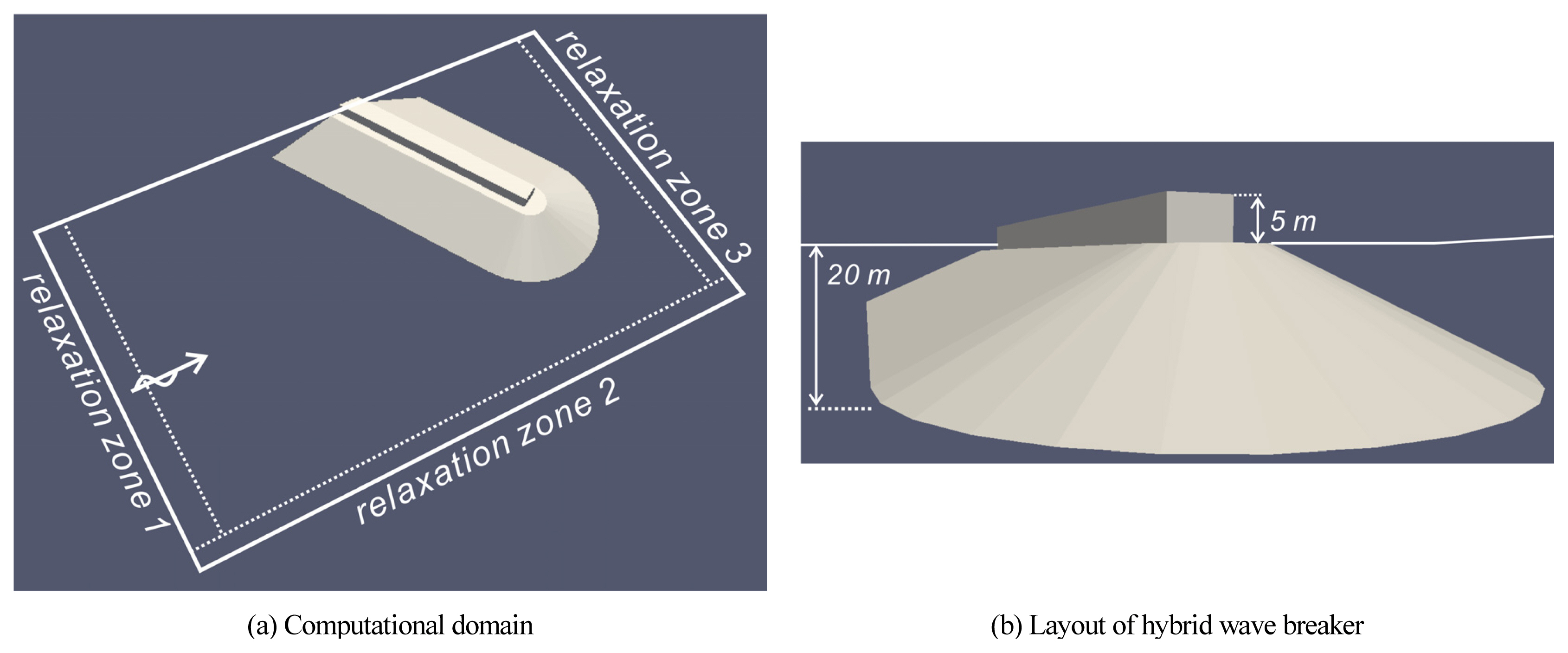
Ēś╝ņä▒ļ░®ĒīīņĀ£ļŖö Ēśäņ×¼ ņÜ░ļ”¼ļéśļØ╝ņŚÉņä£ ļīĆņłśņŗ¼ ļ░®ĒīīņĀ£Ļ░Ć Ļ▒░ņ╣śļÉśļŖö ĒĢ┤ņŚŁņØś ĒĢ┤ņ¢æĒÖśĻ▓ĮņØä Ļ│ĀļĀżĒĢśņŚ¼ 20m ļåÆņØ┤ņØś ņé¼ņäØ Ļ▓Įņé¼ļČĆņŚÉ ļåÆņØ┤Ļ░Ć 5mņØĖ ņ¦üļ”ĮņĀ£Ļ░Ć Ļ▒░ņ╣śļÉ£ ļ¬©ņ¢æņØä ņĘ©ĒĢśņśĆļŗż[Fig. 17 ņ░ĖņĪ░]. Ļ│äņé░ ņśüņŚŁņØ┤ ņŗ£ņ×æļÉśĻ│Ā ļüØļéśļŖö ļČĆļČä[relaxation zone 1, 3]Ļ│╝ ļ░®ĒīīņĀ£ņÖĆ ļ¦łņŻ╝ĒĢśļŖö Ļ│äņé░ņśüņŚŁ ņÜ░ņĖĪ[relaxation zone 2]ņŚÉļŖö sponge layerļź╝ Ļ▒░ņ╣śĒĢśņŚ¼ ļ░®ņé¼ Ļ▓ĮĻ│äņĪ░Ļ▒┤[radiation boundary condition]ņØ┤ ņłśņ╣śņĀü ļ░śņé¼ ņŚåņØ┤ ĻĄ¼ĒśäļÉĀ ņłś ņ׳ļÅäļĪØ ĒĢśņśĆļŗż.
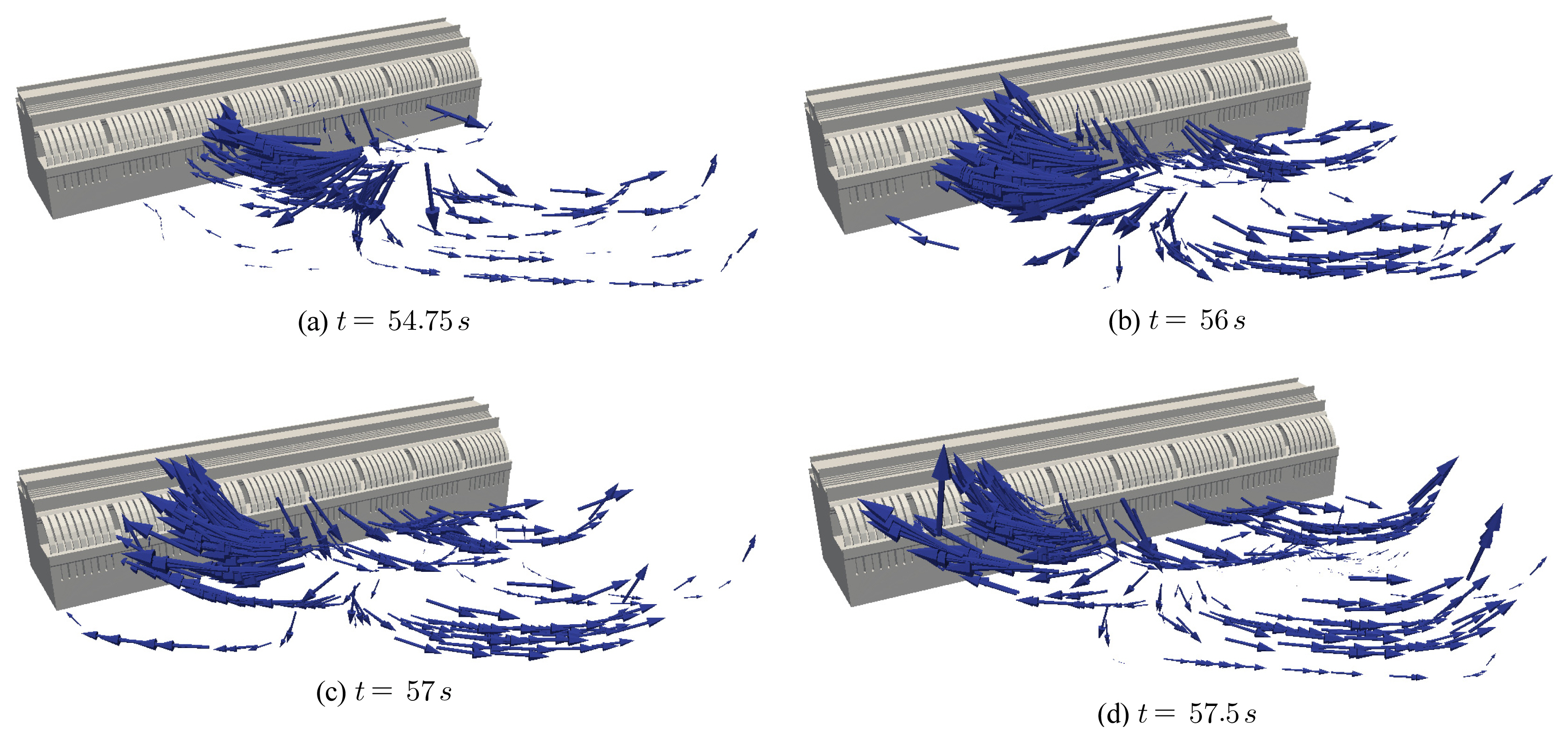
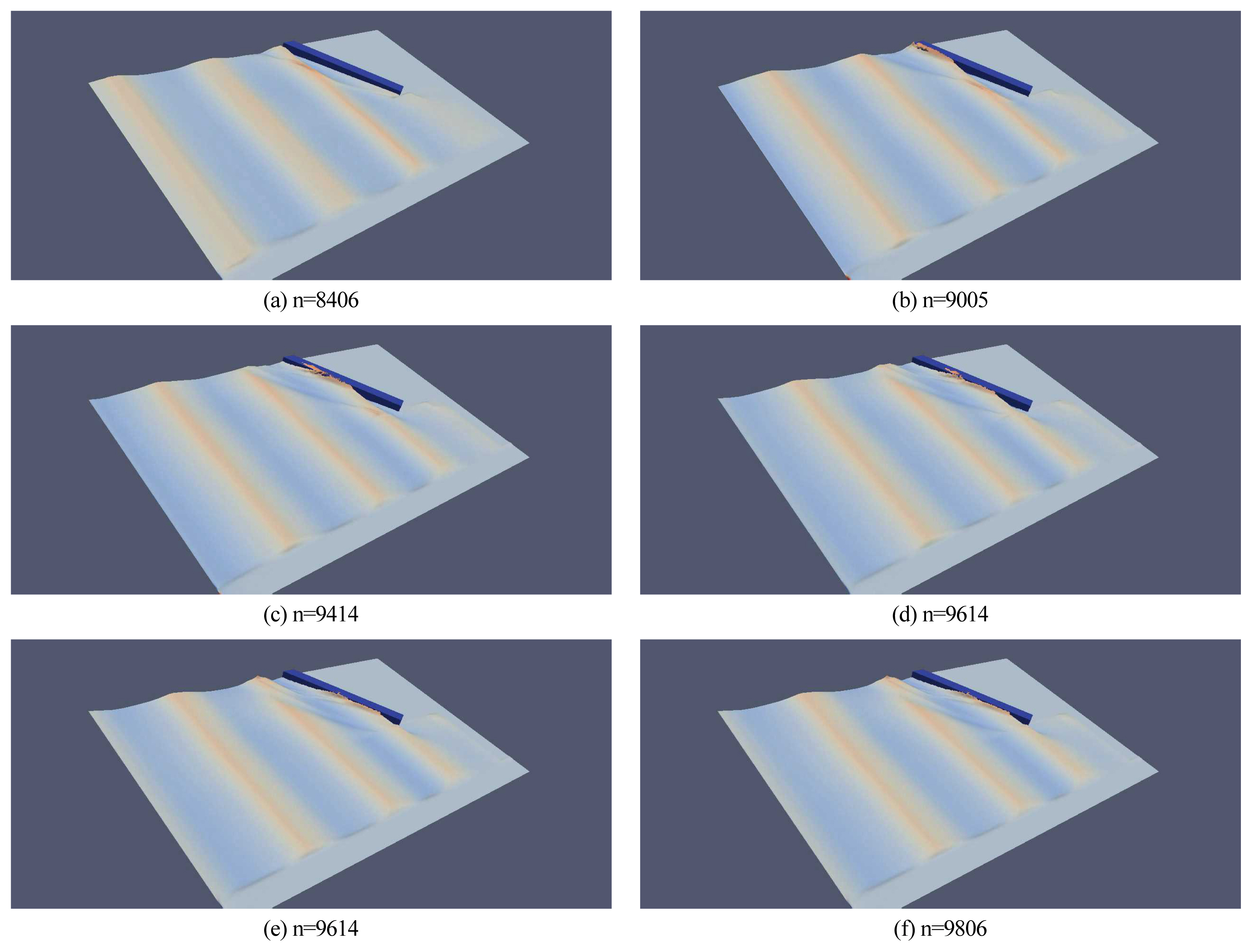
Fig. 18ņŚÉļŖö ņØ┤ĒĢ┤ļź╝ ļÅĢĻĖ░ ņ£äĒĢ┤ ņłśņ╣śļ¬©ņØś ļÉ£ ĒīīļÅÖĻ│ä snapshotņØä ņł£ņ░©ņĀüņ£╝ļĪ£ ņĀĢļ”¼ĒĢśņśĆļŗż. Ēś╝ņä▒ļ░®ĒīīņĀ£ņØś ņé¼ņäØ Ļ▓Įņé¼ļČĆņÖĆ ņ¦üļ”ĮņĀ£ņŚÉņä£ ņ¦äĒ¢ēļÉśļŖö ļ¼╝ļ”¼ņĀü ļ░śņé¼ĒīīĻ░Ć ņłśņ╣śņĀü ļ░śņé¼ ņŚåņØ┤ Ļ│äņé░ ņśüņŚŁņØä ļ╣ĀņĀĖļéśĻ░ĆļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. Ēś╝ņä▒ļ░®ĒīīņĀ£ļź╝ ĻĄ¼ņä▒ĒĢśļŖö ņ¦üļ”ĮņĀ£ņŚÉņä£ ņ¦äĒ¢ēļÉśļŖö ņøöĒīī[Fig. 18 (b), (c), (d), (e), (f) ņ░ĖņĪ░]ļĪ£ ņŚ░Ēīīļź╝ ĒŖ╣ņĀĢĒĢśļŖö Ļ▓ĮņÜ░, ņ¦üļ”ĮņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēļÉśļŖö ņŚ░Ēīīļź╝ ĒÖĢņŚ░ĒĢśĻ▓ī ĒÖĢņØĖĒĢĀ ņłś ņ׳ņ£╝ļéś, ņŚ░Ēīī ņāØņä▒ņśüņŚŁĻ│╝ ņ”ØĒÅŁ ļ╣äļŖö ĒśäņĀĆĒĢśĻ▓ī Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż.
ļśÉĒĢ£ ņé¼ņäØ Ļ▓Įņé¼ļČĆņŚÉņä£ Ļ░ĢņĀ£ļÉśļŖö Ēīīļ×æ ņŚÉļäłņ¦Ć ņåīņé░ņØ┤ ņäĀĒśĢ ĒśĢņāüĒĢŁļĀźĻ│╝ ļ╣äņäĀĒśĢ ĒśĢņāüĒĢŁļĀźņ£╝ļĪ£ ļ╣äĻĄÉņĀü ņĀĢĒÖĢĒ׳ ļ¬©ņØś ļÉśņ¢┤ ņ¦üļ”ĮņĀ£ņŚÉņä£ ņĀĢņĀÉņŚÉ ņØ┤ļźĖ Ēøä ņŗ£ņ×æļÉśļŖö ņ▓śļé┤ļ”╝ Ļ│╝ņĀĢņŚÉņä£ backwash ĒØÉļ”äņØś ņäĖĻĖ░ļŖö ņāüļŗ╣Ē׳ ņĢĮĒÖöĒĢśņŚ¼ ļ░śņé¼ĒīīļŖö ĻĘĖļ”¼ Ēü¼ņ¦Ć ņĢŖļŗżļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż[Fig. 18(i) ņ░ĖņĪ░].
6. Ļ▓░ ļĪĀ
Ēśäņ×¼ ņÜ░ļ”¼ļéśļØ╝ņŚÉņä£ļŖö ĒĢ┤ņāüņØä ĒåĄĒĢ£ ļ¼╝ļÅÖļ¤ēņØś ņ”ØĻ░ĆņÖĆ ņäĀļ░ĢņØś ļīĆĒśĢĒÖöļĪ£ ņ¦üļ”ĮņĀ£ ĒśĢĒā£ņØś ļ░®ĒīīņĀ£Ļ░Ć ņłśņŗ¼ 20m ļé┤ņÖĖņØś ĒĢ┤ņŚŁņŚÉ ņĪ░ņä▒ļÉśĻ│Ā ņ׳ņ£╝ļ®░, ņé¼ņäØ Ļ▓Įņé¼ņĀ£ņÖĆ Ļ▓¼ņżäļ¦īĒĢ£ ņŚÉļäłņ¦Ć ņåīņé░ĒÜ©Ļ│╝ļź╝ ņ¢╗ĻĖ░ ņ£äĒĢ┤ ņ£Āņłśņŗż, ņŖ¼ļ”┐ ļō▒ņØ┤ ņןņ░®ļÉ£ Ļ▓ĮņÜ░Ļ░Ć ļīĆļČĆļČäņØ┤ļŗż. ĻĘĖļ¤¼ļéś ņ£ĀņłśņŗżņŚÉ ĒżĒÜŹļÉ£ Ļ│ĄĻĖ░ņĖĄņØś ņØ┤ņÖäņĢĢņČĢņ£╝ļĪ£ ņāØņä▒ļÉśļŖö ļ░®ņé¼ĒīīļĪ£ ņØĖĒĢ┤ ņ¦üļ”ĮņĀ£ ĒśĢĒā£ņØś ļ░®ĒīīņĀ£ņŚÉņä£ļŖö ņāüļŗ╣ĒĢ£ ļ░śņé¼Ļ░Ć ņ¦äĒ¢ēļÉśļ®░, ļö░ļØ╝ņä£ ņŚ░ĒīīņØś ĒÜ©Ļ│╝ņĀü ņĀ£ņ¢┤ļŖö ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņä▒ļŖźņØä Ļ▓░ņĀĢĒĢśļŖö ņżæņÜöĒĢ£ ņäżĻ│ä ņØĖņ×ÉļĪ£ ļ│┤ņØĖļŗż(Woo, 2016). ņŚ░ĒīīņŚÉ Ļ┤ĆĒĢ£ ĻĖ░ņĪ┤ņØś ņŚ░ĻĄ¼ļŖö ĒĢ┤ņäØņāüņØś ņ¢┤ļĀżņøĆņ£╝ļĪ£ ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņ▓śļ¤╝ Ēīīļ×æņØś ņŚ¼ļ¤¼ ņä▒ņĀĢ ņżæ ņ¦äĒÅŁļ¦īņØä ļŗżļŻ©ļŖö ņŚÉļäłņ¦Ć Ļ│äņŚ┤ Ēīīļ×æ ļ¬©ĒśĢņŚÉ ĻĖ░ņ┤łĒĢ£ ņłśņ╣śĒĢ┤ņäØņØ┤ ņŻ╝ļźśļź╝ ņØ┤ļŻ¼ļŗż. ĻĘĖļ¤¼ļéś ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØ ņ£ĀļÅäĻ│╝ņĀĢņŚÉņä£ ņ░©ņÜ®ļÉśļŖö ņäŁļÅÖļ▓ĢņØä ņāüĻĖ░ĒĢśļ®┤ Ļ▒░ņ╣£ ĒĢ┤ņŚŁņŚÉņä£ļŖö Ļ│Ąņ¦äņä▒ wave-wave interactionņŚÉ ņØśĒĢ┤ ĒīīļÅÖĻ│äņŚÉ ņČ£ĒśäĒĢśļŖö Ļ│Āņ░© ņĪ░ĒÖöņä▒ļČä Ēīīļ×æņ£╝ļĪ£ ņØĖĒĢ┤ ņĀäņłĀĒĢ£ ļ╣äņäĀĒśĢ Schr├Čdinger ļ░®ņĀĢņŗØņØĆ ņśżļźśļź╝ ņłśļ░śĒĢĀ ņłś ņ׳ļŗż.
ņØ┤ļ¤¼ĒĢ£ ņŗ£Ļ░üņŚÉņä£ ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö Navier Stokes ņŗØņØä Ēīīļ×æ ļ¬©ĒśĢņ£╝ļĪ£ ĒĢśļŖö ihFoamņØä ņé¼ņÜ®ĒĢśņŚ¼ ļīĆņłśņŗ¼ ņłśņŚŁņŚÉņä£ ĒØöĒ׳ ņ░©ņÜ®ļÉśļŖö Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņŚ░ĒīīņĀ£ņ¢┤ ĒÜ©Ļ│╝ļź╝ ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ņłśņ╣śļ¬©ņØśļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ļŹöņÜ▒ ņĀĢĒÖĢĒĢ£ ļ¬©ņØśļź╝ ņ£äĒĢ┤ ļ░®ĒīīņĀ£ ĻĖ░ņ┤łļŖö ņ¦Ćļ”ä D50 = 3cmņØĖ ņé¼ņäØņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆņ£╝ļ®░. Ēł¼ņłśņĖĄņŚÉņä£ņØś ņ£ĀļÅÖņØĆ Navier Stokes Eq.ņŚÉ ņČöĻ░Ć ĒĢŁļĀźņØä ļÅäņ×ģĒĢśņŚ¼ ĒĢ┤ņäØĒĢśņśĆļŗż. ņ×ģņé¼ ĒīīĻ│ĀņÖĆ ņŻ╝ĻĖ░ļŖö Ļ░üĻ░ü 3m, 5m, 6.5m, 10.5ņ┤ł, ĒīīĒśĢņØĆ ņłśņŗ¼[h=15m]Ļ│╝ ņŚ░Ēīī ņāØņä▒ Ļ░ĆļŖźņä▒ņØä ļåÆņØ┤ĻĖ░ ņ£äĒĢ┤ Korteweg-de VriesņŗØņØś ĒĢ┤ņäØĒĢ┤ļĪ£ ņĀĢņØśļÉśļŖö Cnoidal waveļĪ£ ņĘ©ĒĢśņśĆļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ļŗżļŻ¼ Ēīīļ×æ ļ¬©ĒśĢņØś Ļ▓Ćņ”ØņØĆ ļŗ©ņł£ ņ¦üļ”ĮņĀ£ļź╝ ļīĆņāüņ£╝ļĪ£ ļ╣äņäĀĒśĢ Schr├Čdinger Eq.ņŚÉ ĻĖ░ņ┤łĒĢśņŚ¼ ņłśĒ¢ēļÉ£ ņłśņ╣śļ¬©ņØśļź╝ ĒåĄĒĢ┤ ņĀĢņä▒ņĀüņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņĪīļŗż.
Ļ▓Ćņ”Ø Ļ▓░Ļ│╝ Cubic Schr├Čdinger ļ░®ņĀĢņŗØņŚÉ ĻĖ░ņ┤łĒĢ£ ņłśņ╣śļ¬©ņØśĻ░Ć ņĄ£ļīĆ ņ”ØĒÅŁ ļ╣äļź╝ ļŗżņåī Ļ│╝ņåīĒĢśĻ▓ī ĒÅēĻ░ĆĒĢśļŖö Ļ▓āņ£╝ļĪ£ ĒÖĢņØĖļÉśņŚłņ£╝ļ®░, ņØ┤ļ¤¼ĒĢ£ ĒśäņāüņØĆ Cubic Schr├Čdinger ļ░®ņĀĢņŗØ ņ£ĀļÅäĻ│╝ņĀĢņŚÉ ņé¼ņÜ®ļÉ£ ņäŁļÅÖļ▓ĢņØ┤ ņ¦ĆļŗłļŖö ĒĢ£Ļ│äņŚÉ ĻĖ░ņØĖĒĢśļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ļśÉĒĢ£ ĒīīĒśĢ Ļ▓Įņé¼ņØś ņÉÉĻĖ░ Ļ░üņŚÉ ļīĆĒĢ£ ņāüļīĆ ļ╣äņ£©ņØ┤ ņ”ØĻ░ĆĒĢśļŖö Ļ▓ĮņÜ░ ņØ┤ļ»Ė ļ│┤Ļ│ĀļÉ£ ņŚ░Ēīī ņāØņä▒ņśüņŚŁņØś ņ”ØĻ░ĆņÖĆ ņ”ØĒÅŁ ļ╣ä Ļ░ÉņåīļŖö ihFoamņŚÉņä£ļÅä ļÅÖņØ╝ĒĢśĻ▓ī Ļ┤ĆņĖĪĒĢĀ ņłś ņ׳ņŚłļŗż.
ņØ┤ņ¢┤ ļīĆ ņłśņŗ¼ ņłśņŚŁņŚÉņä£ ĒØöĒ׳ ņ░©ņÜ®ļÉśļŖö Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś ņŚ░Ēīī ņĀ£ņ¢┤ ĒÜ©Ļ│╝ļź╝ ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ£ ņłśņ╣śļ¬©ņØśĻ░Ć ņłśĒ¢ēļÉśņŚłņ£╝ļ®░, ļ¬©ņØś Ļ▓░Ļ│╝ ņÜ░ļ”¼ņØś ņśłņĖĪļīĆļĪ£ Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ©ņØś ņŚ░Ēīī ņĀ£ņ¢┤ ĒÜ©Ļ│╝ļĪ£ ņ¦üļ”ĮņŗØ ļ░®ĒīīņĀ£ņØś Ļ▓ĮņÜ░ļ│┤ļŗż ņŚ░Ēīī ņāØņä▒ ņśüņŚŁņØĆ ņČĢņåīļÉśĻ│Ā, ņŚ░ĒīīĻ│ĀļŖö 5% ļé┤ņÖĖļĪ£ Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ņĢī ņłś ņ׳ņŚłļŗż. ļśÉĒĢ£ ņ£Āņłś ņŗżņŚÉņä£ ņ¦äĒ¢ēļÉśļŖö ņŚÉļäłņ¦Ć ņåīņé░Ļ│╝ ņØ┤ļĪ£ ņØĖĒĢ£ ļ░śņé¼ņ£© Ļ░ÉņåīļĪ£ ļ░®ĒīīņĀ£ ņĀäļ®┤ ņłśņŚŁņŚÉņä£ Ļ┤ĆņĖĪļÉśļŖö ņĀĢņāü ĒīīļÅÖ Ļ│äļŖö ņ¦üļ”ĮņŗØ ļ░®ĒīīņĀ£ņØś Ļ▓ĮņÜ░ļ│┤ļŗż ļŹ£ ļ¬ģņ¦ĢĒĢśļŗż. ņČ®Ļ▓® ņćäĒīīņĢĢņØś Ļ▓ĮņÜ░, GodaņŚÉ ņØśĒĢ┤ ņØ┤ļ»Ė ļ│┤Ļ│ĀļÉ£ ņé¼ļŗżļ”¼Ļ╝┤ ļČäĒżļź╝ ņČöņóģĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłņ£╝ļ®░, Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ©ņØś Ļ▓ĮņÜ░ņŚÉņä£ ņ¦üļ”ĮņŗØ ļ░®ĒīīņĀ£ņØś Ļ▓ĮņÜ░ļ│┤ļŗż ņČ®Ļ▓® ņćäĒīīņĢĢņØ┤ 15% ļé┤ņÖĖļĪ£ Ļ▓ĮĻ░ÉļÉśļŖö Ļ▓āņ£╝ļĪ£ ļ¬©ņØśļÉśņŚłļŗż. ņØ┤ļ¤¼ĒĢ£ ĒśäņāüņØĆ Ļ│Īļ®┤ ņŖ¼ļ”┐ ņ╝ĆņØ┤ņŖ© ļ░®ĒīīņĀ£ņØś Ļ░£ĻĄ¼ļČĆļĪ£ Ēł¼Ļ│╝ļÉśļŖö ņ£ĀļÅÖņ£╝ļĪ£ ņØĖĒĢ┤ ņÜ┤ļÅÖļ¤ē ņØ┤ņåĪļźĀ[Momentum Flux]ņØ┤ ļČäņé░ļÉśņ¢┤ ļ░£ņāØĒĢśļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
ļ¦łņ¦Ćļ¦ēņ£╝ļĪ£, Ēśäņ×¼ Ļ░ĆņÜ®ĒĢ£ ļ░®ĒīīņĀ£ ņ¢æņŗØ ņżæ Ēīīļ×æ ņŚÉļäłņ¦Ć ņåīņé░ņØ┤ Ļ░Ćņן ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ĆļŖö ņé¼ņäØ Ļ▓Įņé¼ņŗØ ļ░®ĒīīņĀ£ņŚÉņä£ņØś ņŚ░Ēīī ĒŖ╣ņä▒ņØä Ļ░ĆļŖĀĒĢśĻĖ░ ņ£äĒĢ£ ņłśņ╣śļ¬©ņØśļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ņé¼ņäØ Ļ▓Įņé¼ņŗØ ļ░®ĒīīņĀ£ņØś ĒśĢĒā£ļŖö Ēśäņ×¼ ņÜ░ļ”¼ļéśļØ╝ņŚÉņä£ ļīĆ ņłśņŗ¼ ļ░®ĒīīņĀ£Ļ░Ć Ļ▒░ņ╣śļÉśļŖö ĒĢ┤ņŚŁņØś ĒĢ┤ņ¢æĒÖśĻ▓ĮņØä Ļ│ĀļĀżĒĢśņŚ¼ 20m ļåÆņØ┤ņØś ņé¼ņäØ Ļ▓Įņé¼ļČĆņŚÉ ļåÆņØ┤Ļ░Ć 5mņØĖ ņ¦üļ”ĮņĀ£Ļ░Ć Ļ▒░ņ╣śļÉ£ ļ¬©ņ¢æņØä ņĘ©ĒĢśņśĆļŗż [Ēś╝ņä▒ņŗØ ļ░®ĒīīņĀ£, hybrid breaker]. ļ¬©ņØś Ļ▓░Ļ│╝ Ēś╝ņä▒ļ░®ĒīīņĀ£ļź╝ ĻĄ¼ņä▒ĒĢśļŖö ņ¦üļ”ĮņĀ£ņŚÉņä£ ņ¦äĒ¢ēļÉśļŖö ņøöĒīīļĪ£ ņŚ░Ēīīļź╝ ĒŖ╣ņĀĢĒĢśļŖö Ļ▓ĮņÜ░, ņ¦üļ”ĮņĀ£ļź╝ ļö░ļØ╝ ņ¦äĒ¢ēļÉśļŖö ņŚ░Ēīīļź╝ ĒÖĢņŚ░ĒĢśĻ▓ī ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłņ£╝ļéś, ņŚ░Ēīī ņāØņä▒ņśüņŚŁĻ│╝ ņ”ØĒÅŁ ļ╣äļŖö ĒśäņĀĆĒĢśĻ▓ī Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż.






 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print