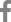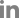|
 |
| J Coast Disaster Prev > Volume 8(4); 2021 > Article |
|
Abstract
As a breakwater gradually becomes obsolete, it becomes vulnerable to loss of its original functions and finally occurs corruption due to cavitation, scours inside, etc. The mortar grouting method, which has been in general applied in many cases, would invoke serious issues such as coastal environmental pollutions because of spilled-out cement before curing on the near sea. Thus, the sand mastic that utilizes the mastic asphalt becomes focused on as a substitute. However, the related study is hard to find in the domestic literature. In this study, therefore, the workability of sand mastic when filling up the cavitation inside a breakwater was evaluated with a 3-D numerical model, FLOW-3D. It was intended to propose the workability index (WI) of sand mastic based on the diffusion diameter. It has been shown that the temperature and the composition ratio of the asphalt are the most significant parameters on the rheologic characteristics of the sand mastic. As a result, it is recommended that the asphalt composition above 16% and the initial temperature above 150℃ when applying with a breakwater with inside cavitation.
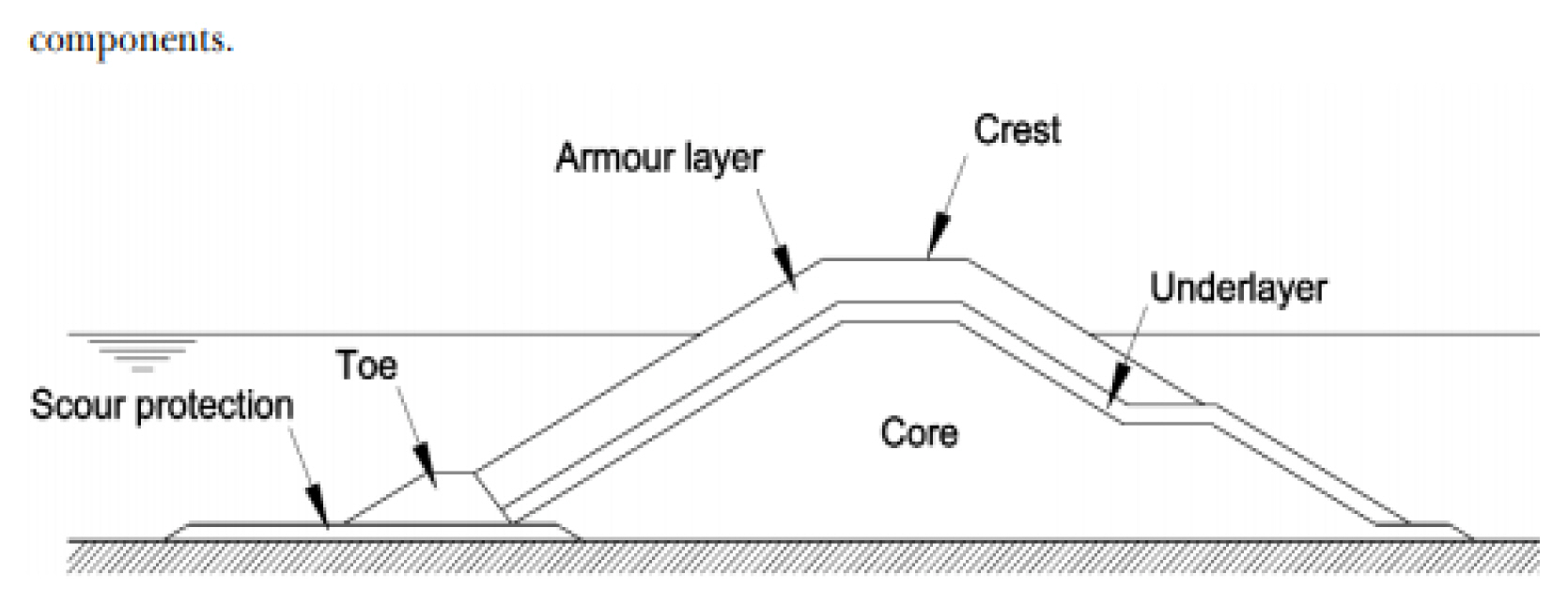
해안구조물은 지속적인 풍파로 인해 세굴이나 침식 등의 손상이 발생하기 쉽다. 특히, 방파제와 같은 외곽시설물은 해안침식작용을 억제하고 주변 주요 시설물을 보호하기 위해 설치되어(Park, 2012), 시간이 경과함에 따라 점차적으로 손상이 누적되며 방파제 내⋅외로 침식이 발생한다. 국내에서는 현재 다양한 형태의 방파제가 축조되고 있으며, 그 중에서 경사제가 많은 비중을 차지하고 있다. Fig. 1은 USACE (1984)에서 나타낸 경사제의 일반적인 구조를 그림이다. 경사제는 재료에 따라서 피복제(Armour layer, Underlayer)와 속채움재(Core)로 구성되어 있으며, 설계파 규모의 파랑이나 지속적인 파랑이 방파제 상부에 큰 파압을 발생시키고 피복제에 손상을 유발한다 (Oh et al., 1999). 피복제에 파손이나 균열이 발생하게 되면 해수가 유입되어 방파제 내부의 속채움재를 유출시키고, 방파제 내부에 빈 공간이 생기게 되며 이러한 공간을 공동(Core failure)이라고 한다(Jung et al., 2021). 내부 채움재가 유출된 공동으로 해수가 유입되면 해수에 포함된 염소이온이 구조물의 산성도를 증가시키고 이는 철근을 부식시킨다. 결과적으로 방파제의 강도를 저하시키며, 붕괴를 유발하게 된다(Page, 1975). 시간이 경과됨에 따라 콘크리트의 염소이온 농도가 높아져 노후화는 구조물의 내구도를 더욱 약화시킨다(Song et al., 2007). 따라서, 해안구조물은 파도와 같은 외부 응력에 의한 손상과 해수에 포함되어 있는 화학물질이 콘크리트 또는 철근과 화학반응을 통한 부식이 동시에 발생할 수 있는 구조물로 지속적인 관심과 대책이 필요하며 특히, 방파제 공동현상에 적절한 채움재를 활용하여 유지⋅보수할 수 있는 방안이 반드시 필요하다.
기존 방파제에 발생하는 공동현상은 몰탈 그라우팅 공법을 주 보수 방안으로 사용하였지만, 몰탈은 일반적으로 60%의 강도를 발현하는데 24시간의 긴 양생시간이 필요하고, 양생되지 않은 해안구조물 내부 공동에 몰탈에 해수가 침투하면 해수희석으로 인해 점착력이 약화되거나 공동 충진 효과가 미확보되는 문제점을 가지고 있다. 또한 해양 생태계로 유실된 몰탈은 바다 석회화 등의 환경문제를 유발시켜 해양생물 및 해안 주변 거주민들에게 악영향을 미칠 수 있다. 따라서, 이에 대한 대안으로 샌드매스틱 아스팔트 혼합물을 보수재료로 사용하는 샌드매스틱 공법을 방파제 등 항만시설물에 활용하는 방안이 국내에도 도입되어야 한다.
샌드매스틱 혼합물은 기존 해외에서 해안에 자주 사용되었고 (Van de Velde et al.(1985)), Van Asbeck(1954)는 샌드매스틱의 물리적인 특징으로 인해 해수 내 위치한 해안구조물에는 아스팔트 등이 유용하게 활용 될 수 있다고 언급한 바 있다. 샌드매스틱 아스팔트 혼합물은 160도 이상의 고온에서 혼합되어 사용되며 지반, 구조물, 수온 등 사용하는 환경에 따라 달라지는 변수에 대한 검토가 필요하며 따라서, 국내 실정에 적합한 샌드매스틱 공법 적용을 위한 조건이 요구된다. 국내에서 도로의 포장에서 주로 사용되는 샌드매스틱 혼합물은 온도에 민감한 재료로 방파제 내부에 공동에 해수가 차있다는 가정 하에 낮은 온도에서 급격히 경화작용이 일어날 수 있다. 본 연구에서는 방파제 내부에 발생하는 공동을 보수하는데 샌드매스틱 공법이 적절히 활용될 수 있는 방안을 모색하고자 샌드매스틱 혼합물의 시공성을 FLOW-3D 수치해석 소프트웨어를 통해 확인하였다. 샌드매스틱 혼합물의 배합 비율 과 온도 등, 샌드매스틱 혼합물의 물성치를 결정하는 요소에 따라 수중 유출 시 수중에서의 샌드매스틱 혼합물의 유동성 및 거동 특성을 수치해석을 통해 파악하였고, 이를 통해 적절한 샌드매스틱 공법 활용 방안을 제시하고자 한다.
본 연구에서는 기존에 사용되었던 몰탈 그라우팅 공법의 대체로 샌드매스틱 공법을 적용하고자 하며 본 공법은 유럽 및 일본에서 적용하고 있는 기술로 국내 환경에 적합하게 개발 중에 있다. 방파제 내부 발생하는 공동의 형상은 매우 불규칙하며 방파제의 규모와 형태에 따라 다양한 형상의 공동이 발생하게 된다. 이러한 원인으로 인해 점성유체의 성질을 띄고 있는 샌드매스틱의 거동의 예측이 어려우며, 이는 보수공사를 설계하는데 있어서 한계점으로 지적되고 있다. 따라서 이에 대해서 다양한 형태의 공동에서 발생하는 샌드매스틱의 거동에 대한 검증이 필요하므로 본 연구에서는 샌드매스틱 공법을 적용함에 있어, 방파제 내부에 유입되는 매스틱 아스팔트 혼합물의 유동성을 수치해석을 통해 적정성을 확인하고자 한다. 특히, 방파제 내부에서 다양한 형태의 공동이 발생하는 점을 반영하기 위해 내부 공동의 형상과 방파제 규모, 형태 등 다양한 환경에 대한 샌드매스틱이 받는 영향을 검토할 필요가 있다.
양생 이전 콘크리트의 거동은 과거부터 수치해석을 통해 계속되어 왔고(Gram, 2009), 본 연구에서도 경제적으로 샌드매스틱 혼합물 거동의 검토를 수행하기 위해 수치해석을 통해 샌드매스틱의 거동을 분석하였다. 아스팔트 함유량과 초기 유출온도에 따라 샌드매스틱은 점성이 변하는 물성을 갖고 있으며, 일반적으로 점성유체의 거동을 나타낸다. Jung et al.(2021)은 낙하된 샌드매스틱의 거동을 수치해석을 통해 연구하였으며, 확산지름의 개념을 적용하여 샌드매스틱의 시공범위를 예측하였다. 실질적으로 샌드매스틱이 국내에서 활용되기 위해서는 국내 방파제에서의 추가적인 특성에 대해 적용할 필요가 있다. 국내의 방파제는 사석층을 갖고 있으며 항만시설 설계기준(2020)에 따르면 방파제 내부 뒷채움재에 사용하는 재료는 주로 주변에서 얻을 수 있는 골재를 사용하고 있어 실질적으로 방파제마다 적용되는 사례가 다르게 나타난다. 따라서 실제 방파제의 설계사례를 적용하여 사석의 분포를 나타냈으며, 홍원항 방파제의 사례를 적용하였다. 해석에 사용되었던 모형은 FLOW-3D 3차원 CFD 모형을 사용하였다.
FLOW-3D는 온도와 시간에 대한 샌드매스틱의 경화를 구현할 수 있으며 연속방정식과 3차원 운동량 보존 방정식, 에너지 방정식을 사용하여 해석한다. 또한 유체의 층류와 난류를 구분하여 해석이 가능하며, 층류 모형, 난류 에너지 모형, k-ε 모형, RNG(ReNomalized Group) 모형, LES 모형 등을 사전에 선택하여 해석이 가능하다(Flow Science, 2018). FLOW-3D의 가장 큰 특징은 직육면체 형상의 격자계를 사용 시 일반 형상 기술의 정확성을 높이기 위해 FAVOR(Fractional Area Volume Obstacle Representation) 기법을 각 방정식에 적용하며, 여기서 비압축성 및 압축성 유체의 해석을 수행할 때 해석속도를 증진시키기 위한 별도의 보조 방정식을 사용한다(Flow Science, 2018). 열전달 및 유체 흐름의 지배방정식은 질량, 운동량, 에너지의 관계를 나타내는 연속방정식, 운동량 방정식 그리고 에너지 방정식이며, 동일한 유체의 범위(system)에서 질량보존 법칙, 뉴턴 제2 법칙, 열역학 제1 법칙이 적용된다. 해석에서는 공간에 고정된 Euler좌표계가 사용하며 3차원 수치해석에 사용된 FLOW-3D는 Eq. (1), Eq. (2)와 같이 유동에 관련된 지배방정식들을 직교좌표계(x, y, z)로 나타낸다.
여기서, u, v, w는 각각 x, y,z 또는 방향의 속도성분을 나타내고, Ax, Ay, Az 는 각 방향의 면적율을 나타낸다. 또 ρ는 밀도, RSOR는 질량 생성 및 소멸항을 나타낸다.
여기서, Gx, Gy, Gz는 체적력(body force)에 의한 가속항이며 fx, fy, fz는 점성 가속항, bx, by, bz는 다공성격벽(porous baffle)과 같은 매질 통과시 유동 감/가속항을 나타낸다.
모형의 검증은 Jung et al.(2021)이 제시한 방식과 동일하게 Kerkhoven(1965)이 수행하였던 실험을 FLOW-3D를 통해 재현함으로써 샌드매스틱의 유동 해석의 적절성을 검증하였다. Kerkhoven(1965)는 샌드매스틱의 점성을 측정하기 위해 Fig. 2(a)와 같이 제시된 Kerkhoven viscometer를 FLOW-3D를 통해 Fig. 2(b)와 같이 재현하였다. Kerkhoven viscometer는 낙하시간에 따라 점성을 추정하는 방식으로 4.0 L의 샌드매스틱이 viscometer 하단에 48 mm의 유출구를 통해 유출되는 시간을 측정한다. 이때 Kerkhoven이 제시한 경험식은 Eq. (3)이며, 낙하시간을 측정하여 점성을 산정할 수 있다. 아스팔트 함유량, 초기온도, 필러의 함유량에 따라서 점성을 측정하는 실험을 진행하였으며, 낙하시간은 Table 1과 같이 나타났다. 낙하시간을 통해 Eq. (3)을 적용하여 산출된 점성은 Table. 2와 같이 나타난다. 이때 수치모형의 점성에 대한 경계조건을 보수적인 검토를 위해 점성의 최대값을 적용하였다. 측정된 시간을 통해 적합도 검정을 수행한 결과 R2값은 Fig. 3(a)와 같이 99.17%로 나타났다. 따라서 FLOW-3D는 샌드매스틱의 점성에 따른 거동을 적절히 나타내는 것으로 판단되며, 최종적으로 Fig. 3(b)와 같이 샌드매스틱의 점성을 초기조건으로 적용하였다.
여기서, η는 점성[Pa∙s], ρ는 샌드매스틱 밀도[kg/m3]이며, 2,100 kg/m3를 적용하였다, g는 중력가속도[m/s2], t는 낙하시간[s]이다.
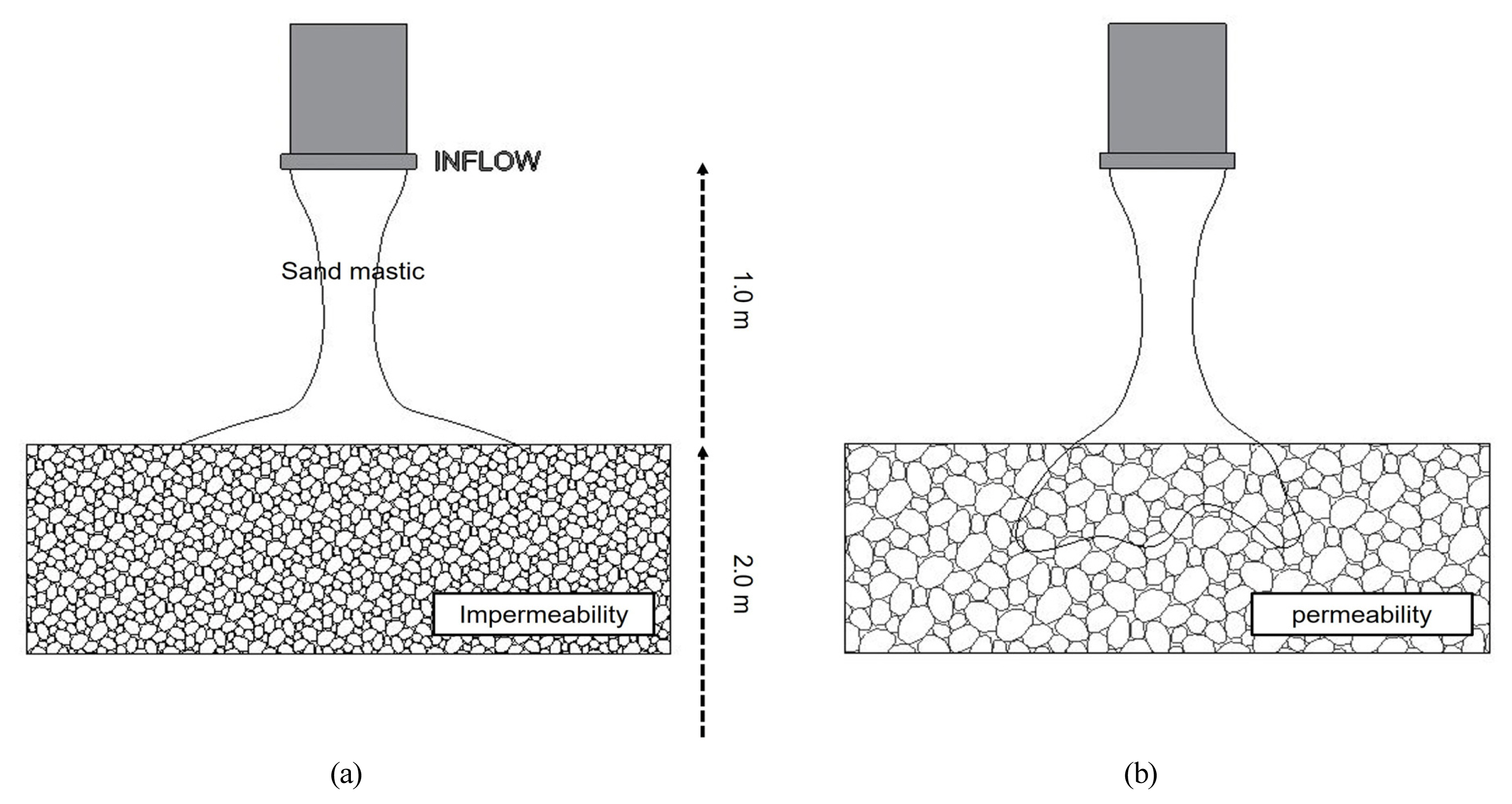
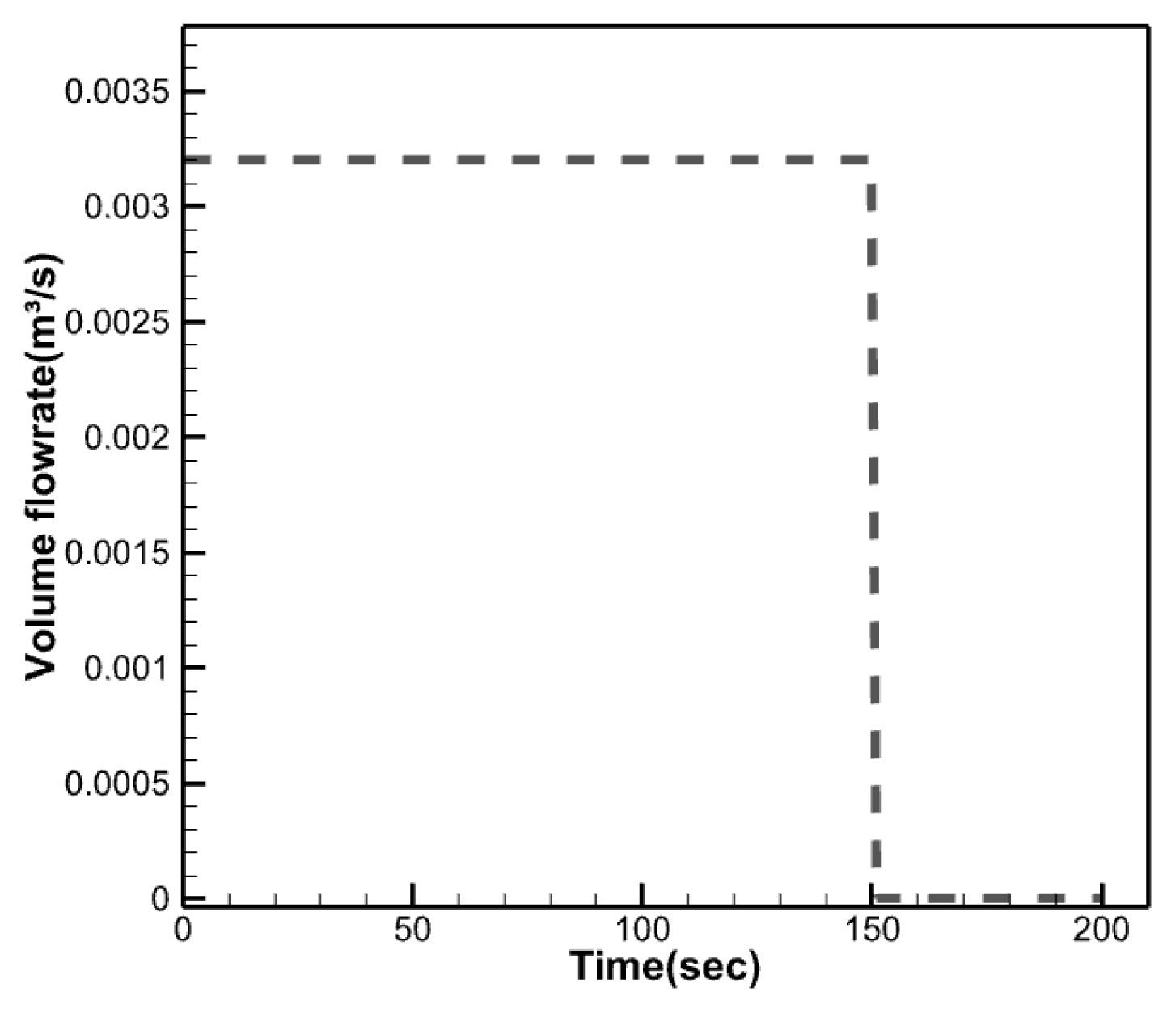
국내에서 설치되는 방파제의 종류는 주로 경사제 형식을 채택하는데, 경사제의 구조를 2가지로 구분하면 외부피복제와 내부사석으로 구성된 속채움재로 구성되어 있다. 이러한 상태의 해석을 수행하기 위해 Fig. 4와 같이 수치해석의 지형자료를 구축하였다. 유출구는 200 mm의 직경을 갖는 원형관이며, 유출구로부터 사석층까지의 높이는 1.0 m로 사석층은 2.0 m 두께를 갖는다. 사석층은 종류에 따라 투과성과 불투과성으로 나뉘는데 사석층에서의 샌드매스틱의 유동은 투과성을 갖는 사석층이며, 측면시공에 대한 검토는 불투과성 지형자료를 사용하였다. 이를 기반으로 아스팔트 함유량 및 초기온도에 변화가 각각 다른 4가지 경우에서의 샌드매스틱의 거동을 해석하였고, Jung et al.(2021)에서 수행한 해석과 동일하게 아스팔트 함유량은 16%와 20%이며, 초기온도는 150℃, 180℃로 구성하였다. 샌드매스틱은 아스팔트 함유량에 따라서 점성이 다르게 나타나며, 이로 인해 샌드매스틱의 온도가 변화함에 따라 점성이 증가하여 최종적으로 굳어버리는 경화현상이 일어나게 된다. 온도에 따른 점성은 실험을 통해 Kerkhoven viscometer로 결정된 점성을 적용하였다. 또한, 방파제 외부피복제가 손상되어 해수의 왕래가 자유로운 상태를 가정하여 해수가 가득찬 상태로 가정하였으며, 초기 수온은 10℃로 국내 평균 해수온도인 13℃ ~ 15℃보다 낮은 온도로 시공환경이 열악한 동계를 기준으로 수온을 선정하였다. 수치해석의 경계 조건인 유량은 기존의 설계(MST, 2020)를 적용하였며 평균 유속은 0.11 m/s으로 적용하였다. 이에 따라서 샌드매스틱의 유량은 11.36 m3/hr를 적용하였다. 총 유출시간은 150 sec이며, 이때 유출되는 샌드매스틱의 총량은 0.47 m3이다. 경화되기 이전까지의 지속적인 샌드매스틱의 유동을 확인하기 위해 유량 이후에도 일정 시간의 경과를 나타낼 수 있도록 수치해석을 수행하였으며, 시간에 따른 유량은 Fig. 5와 같다.
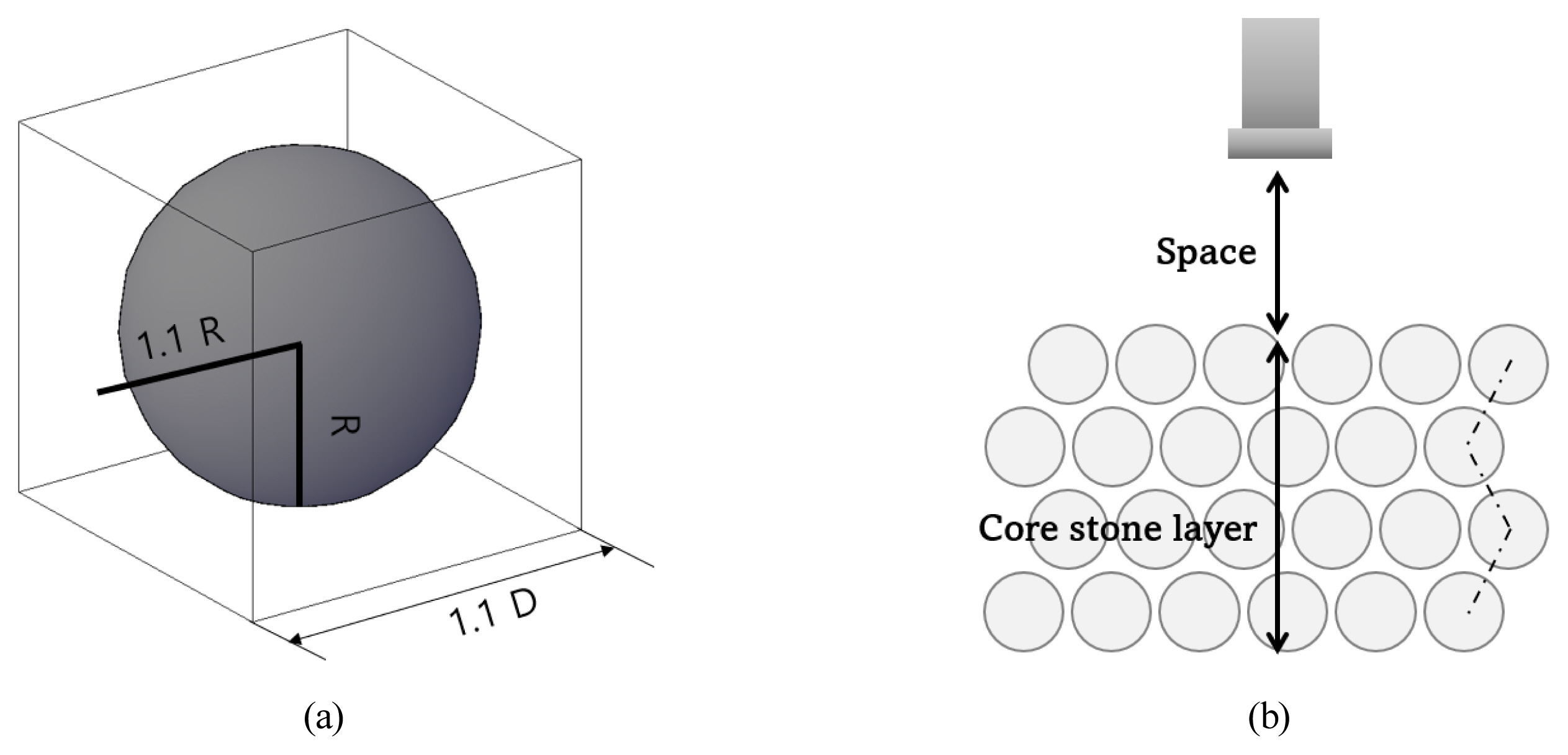
투과성이 있는 속채움재의 사석층을 구성하기 위해 홍원항의 사석 설계기준을 적용하였으며, 사석 설계기준에서 기초사석의 크기는 최소 0.015 m3에서 0.030 m3로 분포하도록 설계되었다. 사석의 형태를 구로 가정하여 수치해석에 적용하는 일정한 크기의 사석의 반지름을 도출한 결과 0.15 m에서 0.20 m의 반지름을 가지며, 이를 통해 0.15 m, 0.17 m, 0.19 m의 지름을 갖는 구로 사석 지형자료를 구축하였다. 기초사석의 배치는 조밀한 구조가 될 수 있도록 일정한 간격으로 지그재그로 배치하여 구성하였으며, 자연 상태에서 해수에 의한 교란 발생을 고려하기 위해 사석과 사석 사이의 간격은 지름의 10%가 유지되도록 배치하였다. Fig. 6(a)는 하나의 사석이 차지하는 공간과 각 크기를 나타내고 있으며, 여기서 R은 사석의 반지름을 나타내며, 하나의 사석은 1.1D를 한 변의 길이로 갖는 정육면체에 하나가 들어가는 형태로 구성된다. 유출높이는 3.0 m 높이로 구성하였다. 유출관경은 기존의 설계에 따라서 최대 관경인 200 mm를 기준으로 설계하였다. Fig. 6(b)는 사석층의 사석의 배치를 나타내고 있으며, 사석층과 유출관 사이의 공간(Space)은 시공과정에서 유출관이 방파제 공동을 통해 유입되므로 높이 1.0 m로 구성하였다.
두 번째로 측면시공에 따른 확산범위를 검토하였으며, 첫 번째 수치실험과 지형자료를 제외하고 동일한 조건으로 해석을 수행하였다. 현장 환경에 따라 방파제 내부 공동의 중심에서의 시공이 불가능한 경우 불가피하게 측면에서 시공이 필요하다. 이러한 상황에서 벽면에 반사되는 샌드매스틱은 평면에 낙하하는 샌드매스틱보다 확산범위가 넓어지므로 시공의 효율을 높이거나, 측면시공의 거리를 예측하는데 사용될 수 있다. 투과성 사석층의 경우 벽면에 의한 반사가 적절히 나타나지 않을 가능성이 있으므로, 벽면 이격거리에 따라 유동성 변화를 분석하기 위해 빈 공간에서의 불투과성 바닥면을 가정하여 확산을 비교하였으며, 확산이 불규칙하게 확산되는 경우를 고려하여 최대 확산거리와 최소확산 거리를 파이프의 중심을 기준으로 xy평면에서의 거리를 측정하였다. 벽면 이격 거리는(1.25 m, 1.00 m, 0.75 m, 0.50 m)를 기준으로 모의를 수행하였다.
방파제 내부 사석층에서의 샌드매스틱의 거동을 예측하기 위해 FLOW-3D CFD모형을 통해 수치해석을 수행하였다. Fig. 7은 직경에 따라서 아스팔트 함유량 16%, 초기온도 150℃의 샌드매스틱의 거동을 나타내고 있으며, 시간이 경과함에 따라 하단부로 샌드매스틱이 대부분 유출되는 양상을 나타내고 있다. 하지만, 일부 사석층 위에서 고착화되어 퇴적되는 양상을 나타내고 있으며, 이를 사석층 내부에서 침투깊이와 사석층 상단에서 퇴적되는 부분으로 나누어 각각의 거동을 검토하였다.
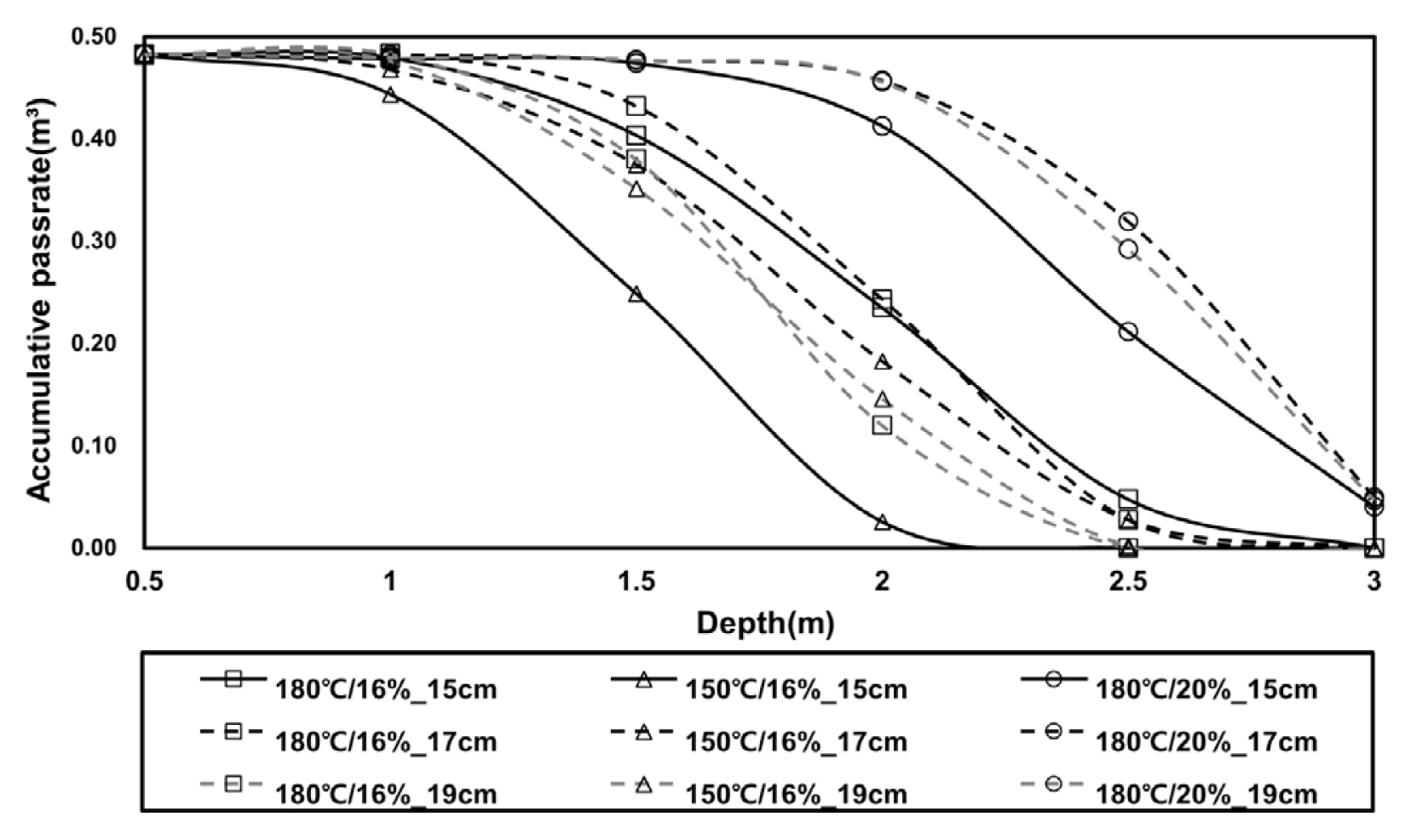
Fig. 8은 유출구를 기준으로 깊이에 따라서 샌드매스틱의 통과량을 나타낸다. 깊이 1.0 m는 사석층이 시작되는 구간으로 아스팔트 함유량이 20%일 때는 대부분의 샌드매스틱이 유하하는 양상을 보이고 있다. 또한 초기조건에 해당하는 샌드매스틱의 초기온도와 아스팔트 함유량이 이 동일한 조건에서 양상이 유사하게 나타나며 사석에 지름마다 약간의 차이를 나타내는 것으로 볼 때, 사석의 지름의 영향보다 샌드매스틱의 유동성을 대표하는 아스팔트 함유량과 초기 온도가 지배적인 것으로 나타났고, 아스팔트 함유량이 온도보다 상대적으로 지배적인 것으로 나타났다.
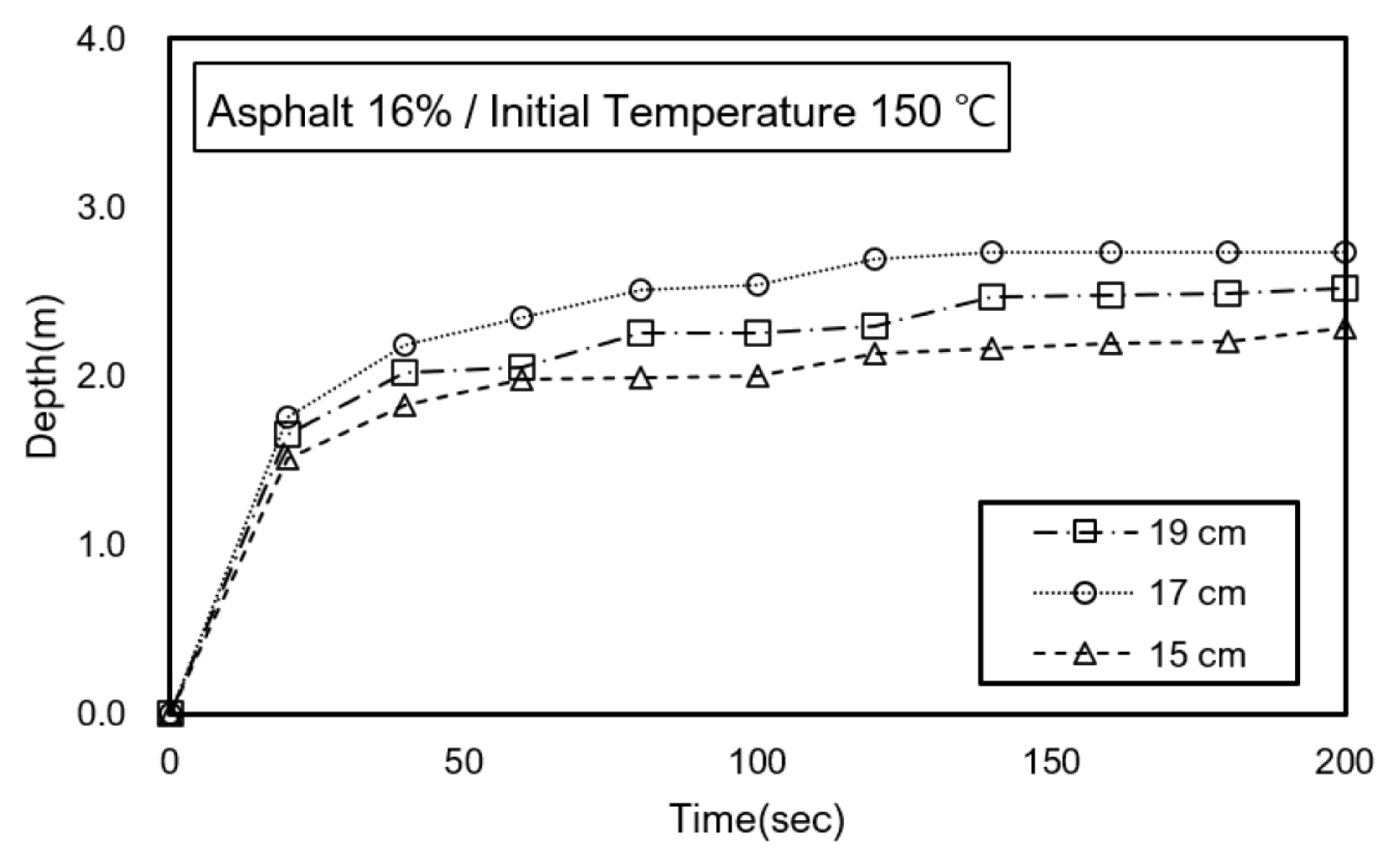
Jung et al.(2021)에 따르면 샌드매스틱의 시공성이 우수한 초기조건은 초기온도 180℃와 아스팔트 함유량 20%인 경우로 제시하였으나, 사석층이 있는 방파제에 시공을 할 때 이와 같은 조건의 샌드매스틱을 사용하게 되면 Fig. 8과 같이 80% 이상의 샌드매스틱이 사석층 내부 1.0 m이상 유출되어 시공성이 떨어지게 된다. 따라서 샌드매스틱이 효과적으로 공동을 채우기 위해서는 1차적으로 유출을 억제할 필요가 있다. 따라서 상대적으로 점성이 높은 아스팔트 함유량 16%의 샌드매스틱을 초기조건 150℃로 유출시켰을 때, 침투깊이를 확인하여 유출을 최소화하는 방안을 적용하였을 때 효과를 확인하기 위해 시간에 따른 침투깊이의 변화를 Fig. 9와 같이 검토하였다. 사석의 크기와 침투깊이는 비선형적인 결과를 나타냈으며, 본 연구에 사용된 사석의 입자크기와는 선형적인 관계를 나타내지 않는 것으로 볼 때 규칙성의 판단이 부적합한 것으로 판단된다. 이러한 결과가 나타난 이유는 샌드매스틱이 유하하면서 접하는 사석의 입자가 충분하지 않은 것이 원인으로 판단되며, 수치 해석에 사용된 사석은 국내 홍원항을 기준으로 결정하였으며, 방파제 보수공사를 진행함에 있어 수치모의 결과 규칙적으로 하단으로 유하하는 샌드매스틱은 실질적으로 불규칙하게 유하할 것으로 판단된다. 또한, 모래나 진흙과 같은 잔골재로 채움재를 구성하였을 때는 입자의 수가 증가하여 선형적인 결과를 나타낼 수 있을 것으로 예상된다. 하지만, 이러한 경우에는 Navier-Stokes 방정식보다는 투수계수를 통한 유량을 산정하는 편이 이론적으로 근사할 것으로 판단된다.
사석층의 상단부의 샌드매스틱의 거동을 확인하기 위해 유출구부터 사석층 상단까지의 구간(0.0~1.0 m) 을 부피와 길이 차원으로 결과를 도출하였다. Table 3은 16%의 아스팔트 함유량을 갖는 샌드매스틱이 사석층 위에 퇴적되는 정도를 채움율로 정의하여 확인하였다. 유효 채움율(Effective filling rate)이란 총 유출된 샌드매스틱 중에서 사석층을 통과하지 않고 사석층 상단에 퇴적되는 샌드매스틱의 양을 비율로 나타내었으며, 이에 따른 형상을 높이와 지름으로 나타냈다. 15 cm의 사석의 지름을 갖는 사석층 상단에서서 공극이 가장 작기 때문에 퇴적높이는 24 cm이며, 퇴적된 샌드매스틱의 지름은 81 cm로 나타났다. 사석의 지름이 15 cm일 때 가장 넓은 면적으로 확산되고 상대적으로 많이 퇴적되었으며 이러한 결과로 볼 때 사석의 크기가 작아질수록 사석층 내부의 공극의 부피가 작아지므로 나타나는 양상으로 보인다. 하지만 유효 채움율이 8%로 사석층 상단을 충진하는 목적의 시공이라면 충분히 효과를 볼 수 없다. 또한 다른 조건의 사석 지름에 대해서도 퇴적높이는 각각 8 cm와 6 cm로 나타났으며, 지름은 5% 이내의 차이를 나타내는 것으로 나타났다. 유효 채움율은 각각 3.0%와 1.3%로 15 cm 사석의 지름을 갖는 조건과 동일하게 사석층 상단을 채우기에 부적합한 것으로 나타났다. 앞서 사석층 내부의 거동에서 검토한 바와 같이 공동을 효과적으로 채우기 위해서는 2차 시공이 불가피할 것으로 판단된다.
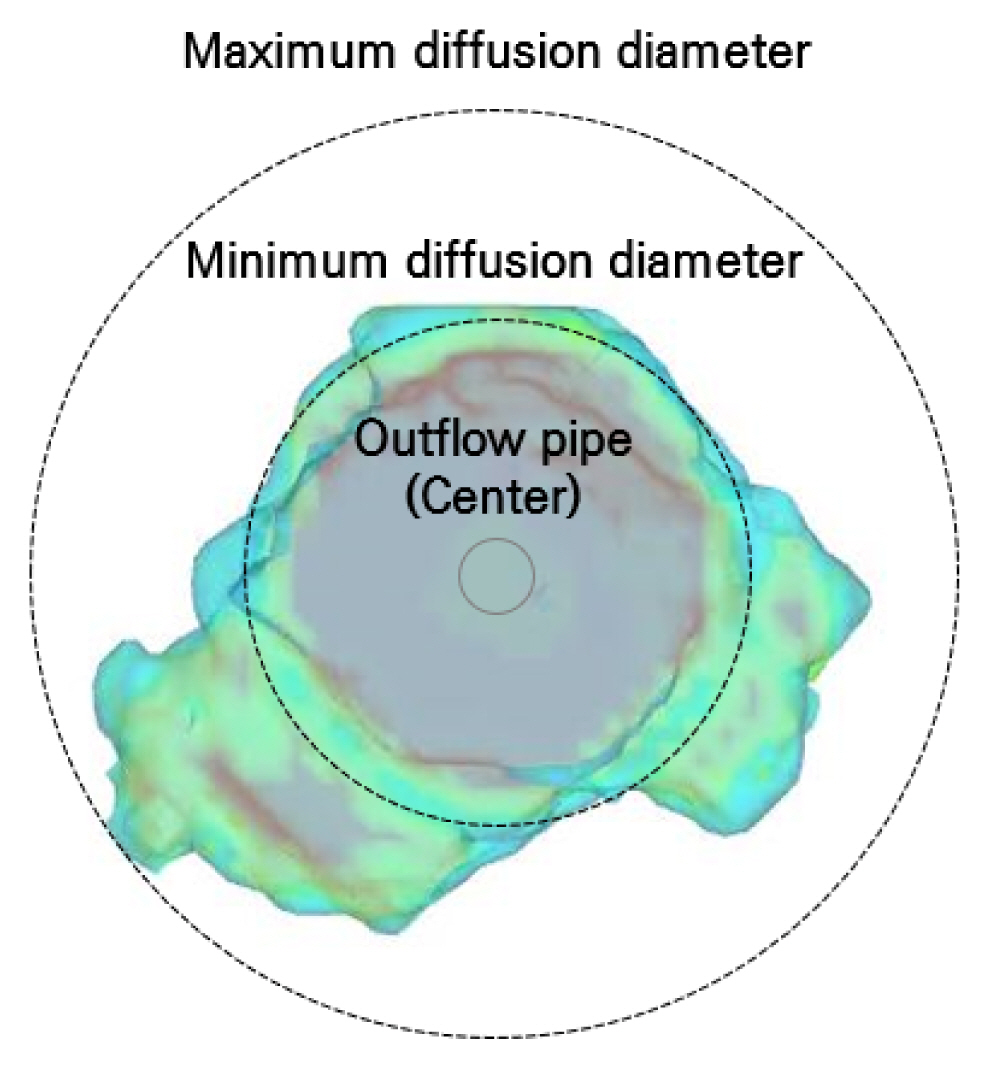
현장시공 시 공동의 중앙지점에서 유출시켜 샌드매스틱을 확산시키는 것이 이상적이지만 경우에 따라 2차 시공 혹은 유출경로에 장애물이 있는 경우에 측면에서 샌드매스틱을 유입할 필요가 있다. 따라서 측면에서 유출할 때 벽면 반사로 인한 샌드매스틱의 유출범위를 산정하였다. 즉, 측면에서 분사할 때 벽이 인접해있는 경우 샌드매스틱의 거동을 확인하기 위해 이격거리에 따른 샌드매스틱의 거동변화를 확인하였다. 불투과성 사석층으로 가정하여 낙하거리는 1.0 m로 설계하였다. Jung et al.(2021)이 제시한 바와 같이 샌드매스틱은 불투과성 벽면에서 발생하는 확산지름은 원형의 형태로 나타나지만 본 연구에서는 벽면에 반사됨에 따라 불규칙적인 확산이 일어나게 된다. 따라서 최대 확산 거리를 나타내는 외심과 최소 확산거리를 나타내는 내심을 통해 Fig. 10과 같이 결과를 도출하였다.
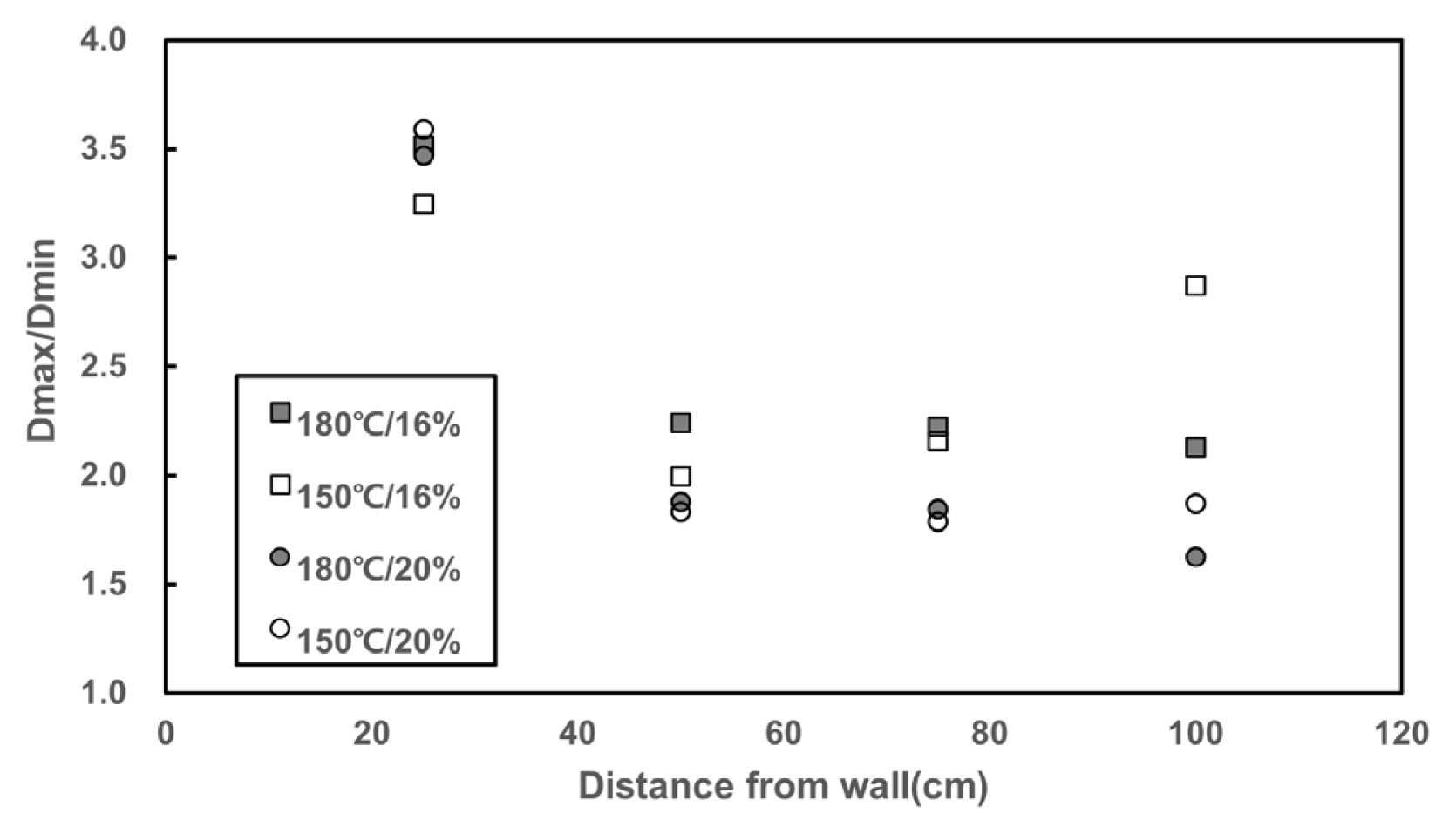
유출된 샌드매스틱의 외심원과 내심원을 아스팔트 함유량 및 초기온도에 따라서 분류하였으며 그 결과는 Table 4과 같이 나타났다. 초기조건과 무관하게 25 cm에서는 모든 샌드매스틱이 벽면에 접하는 결과가 나타났다. 최대 확산지름(Dmax)과 최소 확산거리(Dmin)의 비를 이격거리에 따라 나타낸 결과는 Fig. 11과 같다. 벽과의 이격거리가 멀어질수록 대부분 경우는 비가 점차 감소하는 것으로 나타났으며 이격거리가 커짐에 따라 샌드매스틱의 시공범위의 예측이 용이할 것으로 판단된다. Jung et al.(2021)은 초기 유동성이 샌드매스틱의 확산의 영향이 가장 크다고 언급하였으며, 150℃의 아스팔트 함유량이 16%인 샌드매스틱은 초기 유동성이 낮으므로 불규칙성이 크며 초기 유동성이 상대적으로 높은 다른 조건의 샌드매스틱은 점차적으로 최대 확산지름과 최소 확산지름의 비가 점차적으로 감소한다. 또한 아스팔트 함유량이 20%일 때 이격거리 25 cm를 제외하고 최대 확산지름과 최소 확산지름의 비가 2 이하로 분포하므로 측면시공 시 기존 예상되는 확산지름의 50~65%를 기준으로 시공을 수행하면 공동의 빈공간을 최소화 할 수 있을 것으로 판단되며, 아스팔트 함유량이 16%일 때는 기존 확산지름의 40%를 기준으로 시공을 수행하는 것이 효과적일 것으로 판단된다.
샌드매스틱의 사석층에서 수치해석을 수행한 결과, 20% 아스팔트 함유량의 샌드매스틱은 2.0 m 두께의 사석층을 90% 이상 통과하였으며, 홍원항 설계를 적용한 사석의 범위에서는 사석의 영향이 크지 않음을 확인하였다. 결과적으로 샌드매스틱의 물성치가 더 큰 영향을 미치는 것으로 판단된다. 홍원항에서 사용된 설계 외의 사석의 크기를 적용할 때는 Navier-Stokes 방정식을 기반으로 하는 해석은 불필요하며, Darcy 등 투수계수를 통한 해석이 필요할 것으로 판단된다. 하지만 국내의 대부분 방파제는 항만 및 어항 설계기준(해양수산부, 2020) 등에 나타난 바와 같이 주변에서 취득이 가능한 할석 등을 사용하기 때문에 잔골재로 구성된 사석층에 대한 유동성 검토는 불필요하다고 판단된다. 아스팔트 함유량 16% 샌드매스틱은 사석층 상단에서 퇴적되는 양이 최대 전체 유출량의 8%이며, 나머지는 사석층 내부로 들어가게 된다. 하지만 20%와 다르게 일정 깊이만큼 내려갔을 때는 경화되었으며, 경화된 면 상단으로 퇴적되는 양상으로 나타났다. 따라서, 시공하고자 하는 범위를 근사적으로 예측된 상태에서의 시공이 필요하며 해당 범위가 나타나면 2차에 걸친 시공이 불가피 할 것으로 보인다. 1차 시공을 통해 샌드매스틱의 유하경로를 차단하고 2차 시공을 통해 샌드매스틱을 통한 공극의 채움이 필요할 것으로 보인다. 샌드매스틱의 벽면의 반사율은 벽이 인접한 그라우팅홀에서 시공을 수행할 때 벽에서 가까우면 반대로 시공범위가 넓어질 수 있다. 이를 통해 시공 범위를 적절하게 도출하기 위해 수치해석을 수행하였다. 벽면에서 이격거리에 따라서 25 cm부터 100 cm까지 25 cm 간격으로 이격거리를 구분하였으며, 이때 확산하는 양상이 벽의 영향으로 불규칙하게 나타나므로 외심과 내심의 개념으로 유출구를 중점으로 최대 확산거리와 최소 확산거리를 도출하였다. 내심의 최대값은 벽면 이격거리이며, 25 cm는 앞서 언급하였듯이 벽면에 접하기 때문에 최대 지름이 2배에 해당하는 50 cm로 나타났으며, 다른 경우에는 일정한 값으로 내심이 유지되는 경향을 나타냈다. 또한, 내심이 작아질수록 외심이 커지는 결과가 나타났다. 따라서 외심의 지름과 내심의 지름의 비가 이격거리가 늘어날수록 작아지고 벽면의 영향이 없는 경우 ‘1’로 수렴할 것으로 판단된다. 실질적으로 시공을 수행할 때는 내심의 확산거리를 중점으로 수행을 시행하는 것이 유리할 것으로 판단된다. 샌드매스틱을 국내에 적용하기 위해서는 다양한 경우에 대해 검토가 필요하지만 아직까지 관련 연구가 부족한 실정이다. 향후에는 다양한 조건 및 실제 사례를 통한 적용이 동반되면 샌드매스틱을 통한 효과적인 방파제의 보수공사가 가능할 것으로 판단된다.
Fig. 2
(a) Kerkhoven viscometer design(Kerkhoven, 1965), (b) Representation of Kerkhoven viscometer in FLOW-3D
Fig. 3
(a) Comparison of Kerkhoven viscometer with FLOW-3D, (b) Results of temporal changes of sand mastic viscosity from FLOW-3D

Fig. 7
Comparison of Sand mastic penetration behavior with core stone diameter (Asphalt fraction: 16%/initial temperature 150°C)
Table 1
Results of the sand mastic composition outflow time(sec) at Kerkhoven viscosity meter(Jung et al. 2021)
| Outflow Temperature | Composition of Asphalt | |||||
|---|---|---|---|---|---|---|
| 16% | 20% | |||||
| Composition of Filler | ||||||
| 18% | 22% | 25% | 18% | 22% | 25% | |
| 180°C | 9.8 | 10 | 11 | 4.8 | 6.3 | 3.4 |
| 150°C | 14 | 13.3 | 24.7 | 5.7 | 9.2 | 5 |
| 120°C | 80 | 74 | 42.1 | 34.3 | 12.5 | 17.8 |
Table 2
Viscosity(Pa · s) of the each sand mastic composition(Jung et al. 2021)
| Outflow Temperature | Composition of Asphalt | |||||
|---|---|---|---|---|---|---|
| 16% | 20% | |||||
| Composition of Filler | ||||||
| 18% | 22% | 25% | 18% | 22% | 25% | |
| 180°C | 88 | 90 | 98 | 43 | 56 | 30 |
| 150°C | 125 | 119 | 221 | 51 | 82 | 45 |
| 120°C | 716 | 662 | 377 | 307 | 112 | 159 |
Table 3
Effective filling rate with each core stone diameter
Table 4
Diffusion diameter with initial conditions
References
Flow Science, Inc. 2018 FLOW-3D Version 12.0 Users Manual. FLOW-3D [Computer software] Santa Fe: https://www.flow3d.com. last date accessed: 15 Jul 2021.
Gram, A.. 2009. Numerical modelling of self-compacting concrete flow. Ph.D. dissertation. Royal Institute of Technology (KTH); Stockholm: 53p.
Jung, HJ.. 2021. Workability evaluation of sand mastic for filling cavity in mound breakwater. Master’s thesis. Hongik University; Seoul, Korea.
Jung, HJ., Yoo, HJ., Yang, SL., Lee, SO. (2021). "Numerical simulation of sand mastic asphalt workability for adaptation of repairing the cavitation in the breakwater." Journal of Korean Society of Coastal Disaster Prevention, Vol. 8, No. 2, pp. 88-97. (in Korean with English abstract).

Kerkhoven, RE. (1965). "Recent developments in asphalt techniques for hydraulic applications in the Netherlands." Association of Asphalt Paving Technologists Proceedings, Vol. 34, pp. 538-573.
Ministry of oceans and fisheries. (2020). Engineering design Standard for Harbor and fishery port, Ministry of oceans and fisheries in Korea.
Oh, BH., Jang, BS., Jang, SY., Jeon, SJ., Yu, Y., Park, DG., Hyeong, SS. (1999). A study on the effects of seawater on the durable life of concrete structures (II). KINS/HR—218, Korea Atomic Energy Research Institute, 40p.(in Korean).
Oh, SH., Oh, YM., Yeo, BG., Han, TY. (2014). "A case study of comparing formulae for estimating horizontal wave force on crown wall of sloping breakwater." Journal of Korean Society of Coastal Disaster Prevention, Vol. 1, No. 1, pp. 28-35. (in Korean with English abstract).
Page, CL. (1975). "Mechanism of corrosion protection in reinforced concrete marine structures." Nature, Vol. 258, No. 5535, pp. 514-515.

Park, SG. (2012). Coastal and harbor engineering. Munundang, 339p.(in Korean).
Song, HW., Lee, CH., Ann, KY. (2007). "Factors influencing chloride transport in concrete structures exposed to marine environments." Cement and Concrete Composites, Vol. 30, No. 2, pp. 113-121.

USACE. (1984). Shore protection manual Volume 2, Coastal Engineering Research Center, Department of the army US Army Corps of Engineers.
Van Asbeck, BW. (1954). "Bitumen in coastal engineering." Coastal Engineering Proceedings, Vol. 1, No. 5, pp. 587-620.

Van de Velde, PA., Ebbens, EH., Van Herpen, JA. (1985). The use of asphalt in hydraulic engineering, Rijkswaterstaat, 306p.



 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print