1. 서 론
IPCC(Intergovernmental Panel on Climate Change) 3차 보고서(IPCC, 2001)에서는 인간 활동으로 인해 21세기에 지구온난화가 가속화되고 있음을 밝혀냈으며, 4차 보고서(IPCC, 2007)에서는 이로 인해 2100년까지 전지구의 해수면이 60cm 상승할 것으로 전망하였다. 해수면의 상승은 침수, 연안 침식, 염해 등 광범위한 사회경제적 피해를 유발하는 만큼 파도, 조류로부터 육지를 보호하는 해안 시설물인 방조제의 운영에도 상당한 영향을 끼칠 것으로 예상된다. 해수면 상승에 따른 외력조건(해수면상승, 파고증가 등)이 증대하게 되면 방조제는 태풍, 해일 등 자연재해에 취약성이 높아지기 때문에 안전성 확보 방안 및 장기적인 대책 수립이 필요하다(Park et al, 2015). 새만금 방조제는 대한민국 전라북도 부안군과 군산시를 연결하는 초대형 둑으로 길이는 33.9km로 세계에서 가장 긴 것으로 기네스월드레코드에 등재되었다. 1991년 11월에 착공하여 2010년 4월에 준공하였다. 새만금 방조제는 폭이 평균 290m(최대 535m)이고, 높이는 평균 36m(최대 54m)에 이르는 대형해상구조물로서, 대부분 물속에 잠겨있고 바깥에 드러난 부분은 평균해수면 위로 약 1m이다. 기후변화에 의한 해수면상승은 이러한 대형해상구조물의 운영에도 상당한 영향을 끼칠 것으로 예상되므로 방조제 운영을 위해서는 미래 해수면 변동 특성의 분석이 필요하다.
최근 수십 년간 해수면 변동 경향성은 자료의 주기적 특성을 사용하여 추정되었으며, 다중스케일 분석 방법을 적용하여 해수면 자료로부터 다양한 스케일이 존재하는 시계열을 산출할 수 있다. 해수면 자료는 다양한 지구물리학적 원인에 의해서 변동하며, 비선형적 또는 준주기(quasi-periodic)의 형태를 가진다. 이러한 경우 다중스케일 분석을 통해 주기별로 성분을 분리할 수 있는 장점이 있으며, 특히 비정상성(경향성) 성분과 주기성분을 분리할 수 있기 때문에 기후 변화로 인한 시계열의 증가 현상을 효과적으로 추출하여 평가할 수 있다. 즉, 일반적으로 분해되는 다양한 스케일의 시계열 중에서 제일 긴 주기의 시계열을 자료의 경향성으로 가정한다. 다중스케일 분석은 주기특성을 분해하는 과정에서 기저함수를 이용하는 결정적 방법과 자료에 내재한 주기를 경험적으로 추출하는 경험적 방법으로 나눌 수 있다. 본 연구에서는 선형회귀분석 방법, 연속 웨이블릿 변환(CWT, Continuous Wavelet Transform) 방법, 앙상블 경험적 모드 분해(EEMD, Ensemble Empirical Mode Decomposition) 방법을 사용하였다.
2. 연구방법
본 연구에서의 해수면 상승을 위한 분석체계는 크게 두 가지로 나눌 수 있다. 첫째는 관측 조위를 활용하여 경향성 분석을 수행하고 이를 미래전망을 위한 정보로 활용하는 것이다. 이를 위해서 선형회귀분석 방법, CWT 방법, EEMD 방법을 활용하여 관측조위로부터 장기적인 경향성을 추출하고 미래전망에 이용하였다. 둘째는 우리나라를 포함하여 기후변화 영향을 평가하기 위한 전지구 기후모형의 해수면 상승 시나리오를 활용하는 것이다. 이를 위해서 본 연구에서는 전지구 기후변화 시나리오 제공을 위한 국제 프로젝트인 CMIP5(Coupled Model Intercomparison Project-5)에서 제공하는 기후변화 시나리오로부터 우리나라 주변의 해수면 상승 시나리오를 추출하고 평가에 활용하였으며, 최종적으로 국립해양조사원의 관측조위 기반의 선형회귀분석 결과와 비교하여 분석하였다.
2.1 연속웨이블릿변환 방법
웨이블릿 변환(Wavelet Transform)은 기저함수(basis function)의 스케일항(scale)과 전이항(translation)이라는 두 변수로 표현되고 시계열의 서로 다른 스케일 성분들로 분해 가능하다. 여기서 스케일은 주파수 영역에서의 우리가 평가하고자 하는 주파수를 의미한다. 즉, 스케일 항을 이용하여 기저함수의 폭을 축소 또는 확대하여 변환시킴으로써 고빈도(high frequency)에서 저빈도(low frequency)에 해당하는 다양한 주파수 영역에서 시계열의 주기를 평가하게 된다. 전이항은 시간에 따른 각 주파수가 가지는 스펙트럼의 강도를 평가하기 위해서 도입된 항으로서 전이항을 우리가 원하는 시간으로 이동시키면서 시간에 따른 주기의 강도를 평가할 수 있다. 이러한 점에서 기존에 신호 데이터 분석에 많이 사용되던 FFT(Fast Fourier Transform)와는 다르게 시간에 따라 변동하는 주기의 강도를 용이하게 평가할 수 있으며 시간 영역의 해상도와 주파수 영역의 해상도를 시간과 주파수 영역에서 전체 또는 지역적인 특징도 분석 가능한 특성을 지닌다. 이러한 Wavelet Transform의 특성들은 2차원 영역의 복잡성을 효과적으로 분석할 수 있으며 시계열분석에 있어 또한 많이 활용된다.
Wavelet Transform의 기저함수는 특별한 형식이 정해져 있지 않으며 기저함수가 될 수 있는 조건만 충족하면 되기 때문에 각 주파수 영역에 따라 변화하는 다양한 기저함수가 존재한다. Eq. (1)은 Wavelet Transform의 기저 함수를 나타내며 여기서 sc는 스케일을 결정하는 값이고, sh는 함수를 얼마나 이동시킬 것인가의 전이항을 의미한다.
Wavelet Transform의 기저 함수로 사용되는 Ψ(t)를 모(Mother) Wavelet 함수라고 하며 다음의 Eqs. (2) and (3)의 두 가지 조건을 만족시키면 Mother Wavelet 함수가 될 수 있다.
Wavelet Transform은 Eq. (1)에서 Mother Wavelet을 sh만큼 이동하고 sc에 의해 크기를 변화시켜가는 기저 함수를 사용한다. 이는 고빈도(high frequency)로 갈수록 Wavelet은 함수의 폭이 좁아지고, 저빈도(low frequency)로 갈수록 함수의 폭이 넓어지는 것을 나타낸다. Wavelet Transform은 Wavelet 기본 함수들의 중첩으로 임의의 함수를 표현하는 것인데 이러한 Wavelet 기본 함수들의 중첩은 각각 다른 스케일 레벨을 가지고 임의의 함수를 만들어 내며, 각 레벨은 그 레벨에 맞는 해상도를 가지게 된다. 연속적인 신호의 Wavelet Transform은 Eq. (4)와 같이 정의되며 그것의 역변환은 Eq. (5)와 같이 정의된다. 여기서 X(t)는 원자료를 나타내며 W(sc,sh)는 에너지 스펙트럼을 의미한다. Ψ*는 Ψ의 켤레복소수를 의미한다. 여기서 Ψ(w)는 Fourier Transform Ψ(t)의 값을 의미하며, w는 주파수를 나타낸다.
일반적으로 CWT방법에서 스펙트럼 추정 시에 효율적인 방법은 이산(Discrete) Fourier Transform (DFT)을 이용해서 Fourier Transform 영역에서 스펙트럼을 추정하는 것이다. DFT의 Convolution 이론에 근거하여, Wavelet Transform은 Fourier Transform의 역변환과 같으며 다음 식과 같이 나타낼 수 있다.
여기서 X ^ k Ψ ^ * ( s w k )
여기서 s0는 추출 가능한 가장 작은 스케일을 나타나며 δj는 추출 간격을 의미하고 Mother Wavelet 함수의 특성에 따라 다른 값을 나타낸다.
CWT 방법은 자료의 특성에 따라 선택되는 Mother Wavelet에 의해 분해가 이루어지며, 잡음(Noise Level)과 상관없이 다중스케일 분석이 가능한 장점이 있는 반면, 사용된 Mother Wavelet이 자료의 특성과 잘 맞지 않는 경우 문제가 될 수 있다.
2.2 앙상블 경험적 모드 분해 방법
경험적 모드분해(EMD, Empirical Mode Decomposition) 방법은 체거름 알고리즘(sifting algorithm)을 통해 주어진 자료에 내재한 다양한 주기인 내재모드함수(Intrinsic Mode Function; IMF)와 주기적 특성을 뺀 나머지인 잔여값(residual)으로 분해하는 방법이다 (Lee et al, 2019). 따라서 잔여 값으로부터 자료가 가진 고유의 장기적 경향성을 알 수 있다. EMD 방법을 통해 분해된 IMF는 전체 자료계열에서 극값(최댓값 및 최솟값)의 개수와 부호변화점(zero crossing)의 개수는 같거나 최소 1이어야 하고, 어느 지점에서도 상위선과 하위선의 평균은 0이어야 한다는 두 가지 조건을 만족해야 한다. 주어진 시계열 자료를 분해하는 체거름 과정은 아래와 같다.
(1) 주어진 시계열 자료가 y(t),t = 1,2,3, ...,n일 때 극값을 식별한 후 삼차 스플라인(cubic spline) 보간법을 이용하여 각각 상위선(upper envelope, yu (t))과 하위선(lower envelope, yl (t))을 구한다.
(2) 상위선과 하위선의 평균선(mean envelope, ym (t) = (yu (t) + yl (t))/2)을 구한다.
(3) 원자료계열 y(t)에서 평균선을 공제한 후(y(t) -ym(t))의 자료계열이 IMF 조건을 만족할 경우 이를 추출된 IMF IMFi라 정의한다.
(4) (3)에서 추출된 IMF를 제거한 후의 시계열을 원자료 계열 y(t)로 재설정하고, 남은 자료계열이 단조함수 또는 하나의 극값만 존재하여 더이상 새로운 계열이 추출되지 않을 때까지 (1)~(3)의 과정을 반복한다.
(5) 최종적으로 원자료계열 y(t)는 다음 식과 같이 분해된 모든 IMF(IMFi)의 합과 잔여값(residual)의 합으로 나타낼 수 있다. 여기서 N은 추출된 IMF의 개수이다.
EMD 방법을 통해 자료를 분해할 경우, mode-mixing 문제가 발생하므로 이를 해결하기 위해 개발된 방법이 앙상블 경험적 모드 분해(EEMD) 방법이다. EEMD 방법은 주어진 자료에 인위적으로 백색잡음(white noise)을 추가하고 자료를 분해한 후 잡음을 제거하는 방법으로, 자료 분해를 수행하면 마지막에 추출되는 residual은 자료에 내재한 장기 경향성(long-term trend)을 나타낸다. Fig. 1은 EEMD 방법 적용을 위한 과정을 설명하였다.
EEMD 방법의 경우 경험적으로, 즉, 반복적 과정을 거처 자료의 주기를 추출하는 모형으로서 사용되는 Mother Wavelet 따른 CWT 방법의 단점을 보완할 수 있다. 다만 자료에 잡음이 많은 경우 결과를 정확하게 분석하지 못하는 단점이 존재한다.
3. 조위관측자료 기반 해수면 상승 경향성 분석
국립해양조사원은 총 132개 관측소로 이루어진 국가해양 관측망을 운영하고 있으며, 조위관측소 50개소와 해양관측소 3개소, 해양과학기지 3개소에서 실시간으로 분 단위 해 수면을 관측하고 있다. 본 연구의 대상 지역인 군산 (새만금 방조제 소재지)의 조위관측소 중에서 관측기간이 30년 이상이며 결측치가 5% 미만의 6개 지점의 자료를 사용하였다(Fig. 2 and Table 1).
3.2 CWT와 EEMD 분석
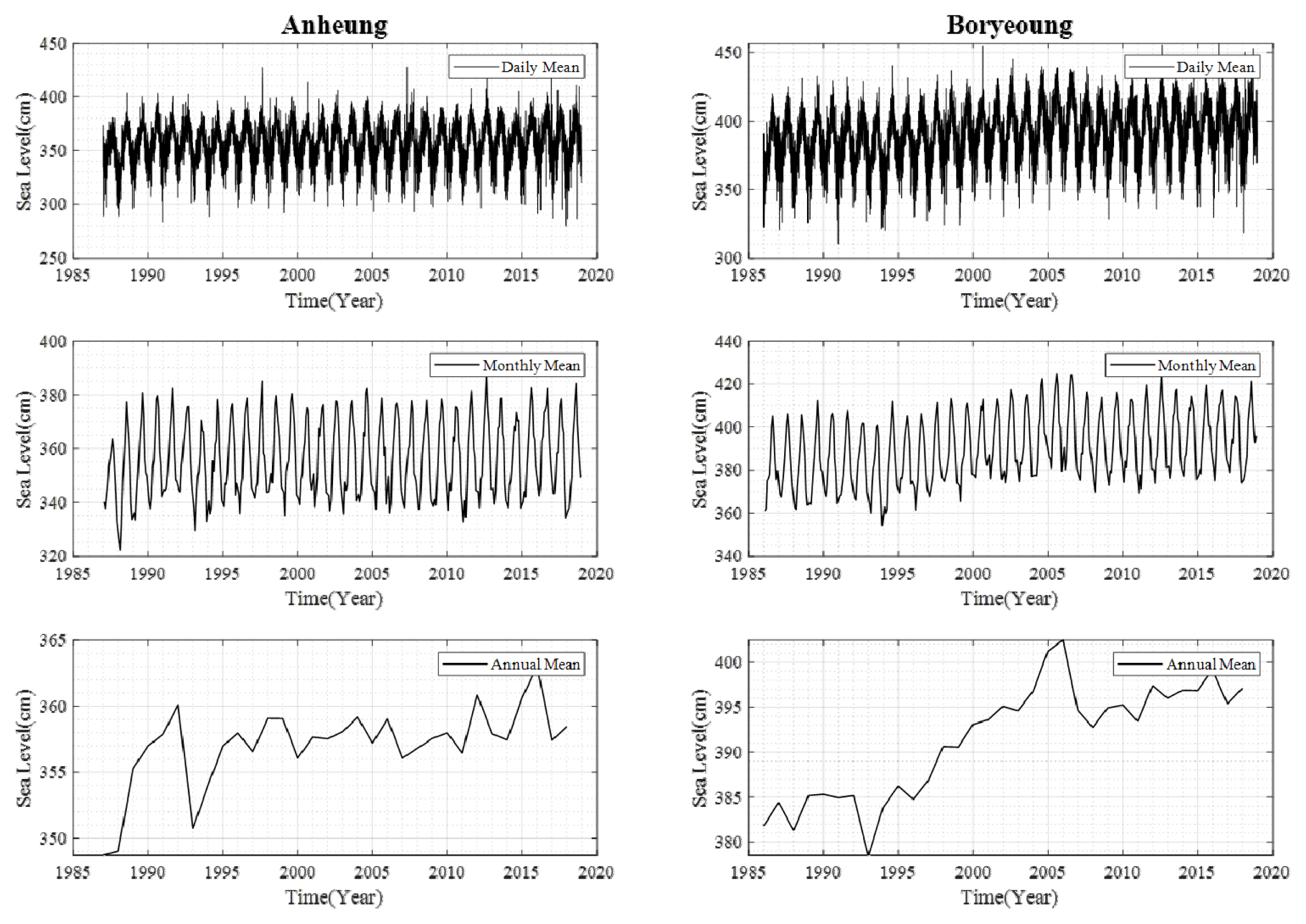
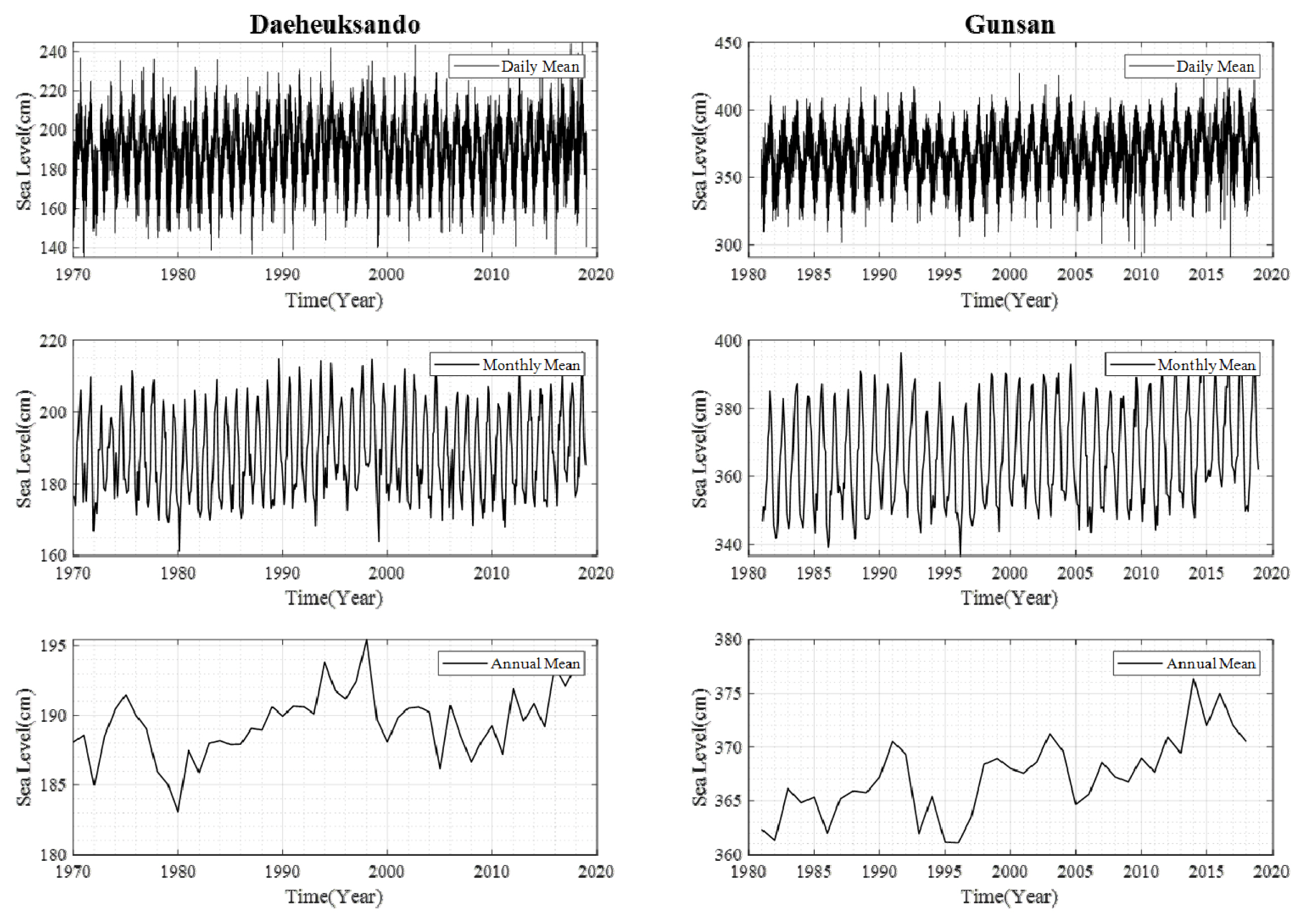
Table 1의 국립해양조사원 관측소 지점들로부터 획득한 해수위 관측자료를 활용하여 해수면 상승 경향성을 분석하기에 앞서 일평균 해수위, 월평균 해수위, 연평균 해수위의 전체적인 양상을 확인하였다(Figs. 3, 4 and 5). 이상치(outlier)의 제거를 위해 원자료의 평균으로부터 ±4표준편차 범위(자료 분포의 99.9%) 내에 드는 값만을 취하였다(Ilyas and Chu, 2019).
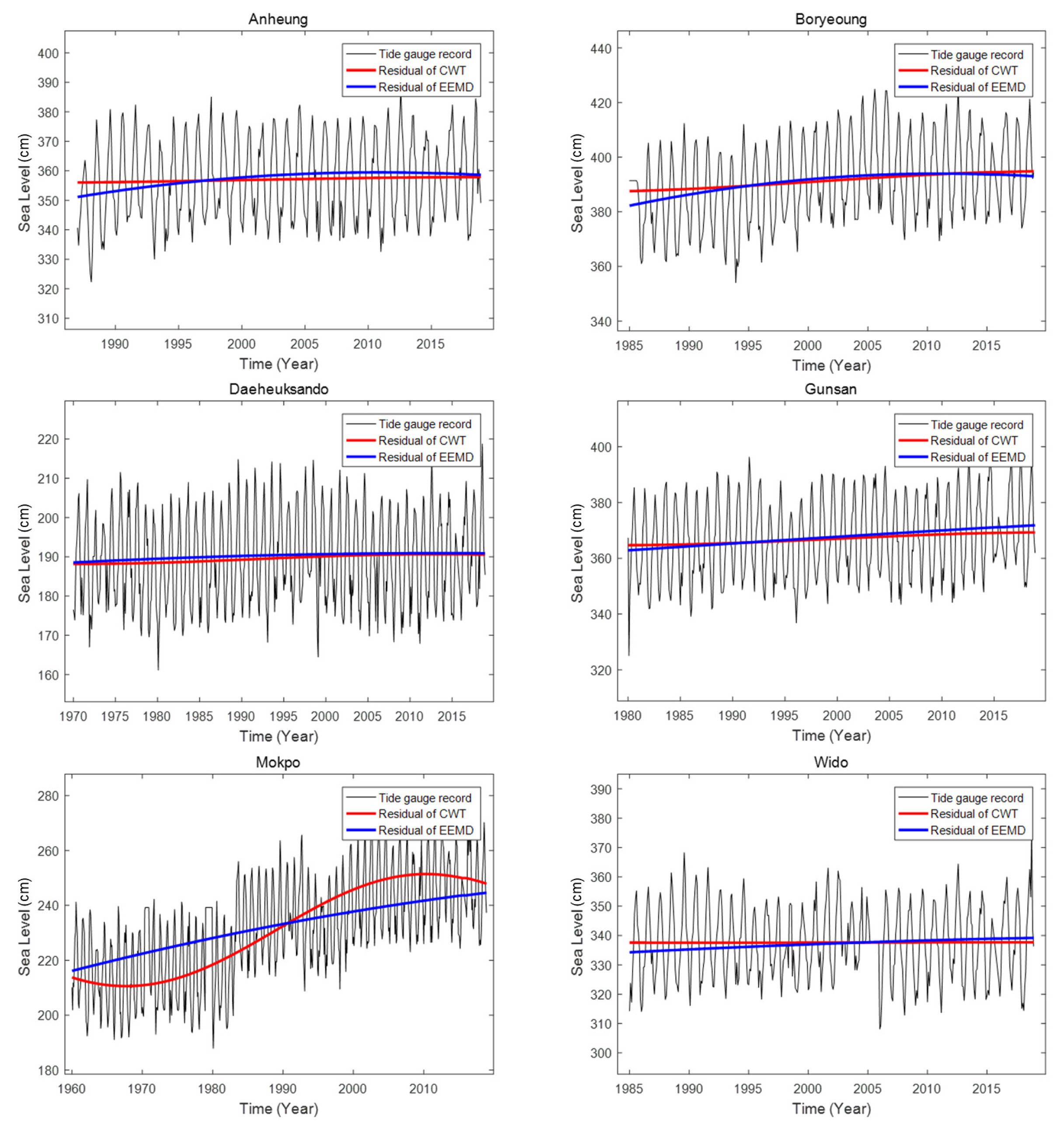
본 연구에서는 EEMD 방법에 noise 진폭 Rstd = 0.2, 예상 앙상블 개수 Nens = 300를 사용하였고(Wu and Huang, 2009), CWT 방법에는 모함수 Morlet를 선택하였고 파의 개수 ω0 = 6으로 하였다(Farge, 1992). CWT와 EEMD 방법으로 추출된 residual에 대하여 2차식 적합(fitting)을 통해 경향성을 추정하였다. 일반적으로 추출된 residual은 sigmoid 곡선 형태이며 sigmoid 곡선에는 2차 다항식이 다른 방법들에 비해 가장 적합하다고 알려져 있다. Fig. 6은 CWT와 EEMD 방법에 의한 6개 지점들의 해수면 상승 경향성을 나타내었다.
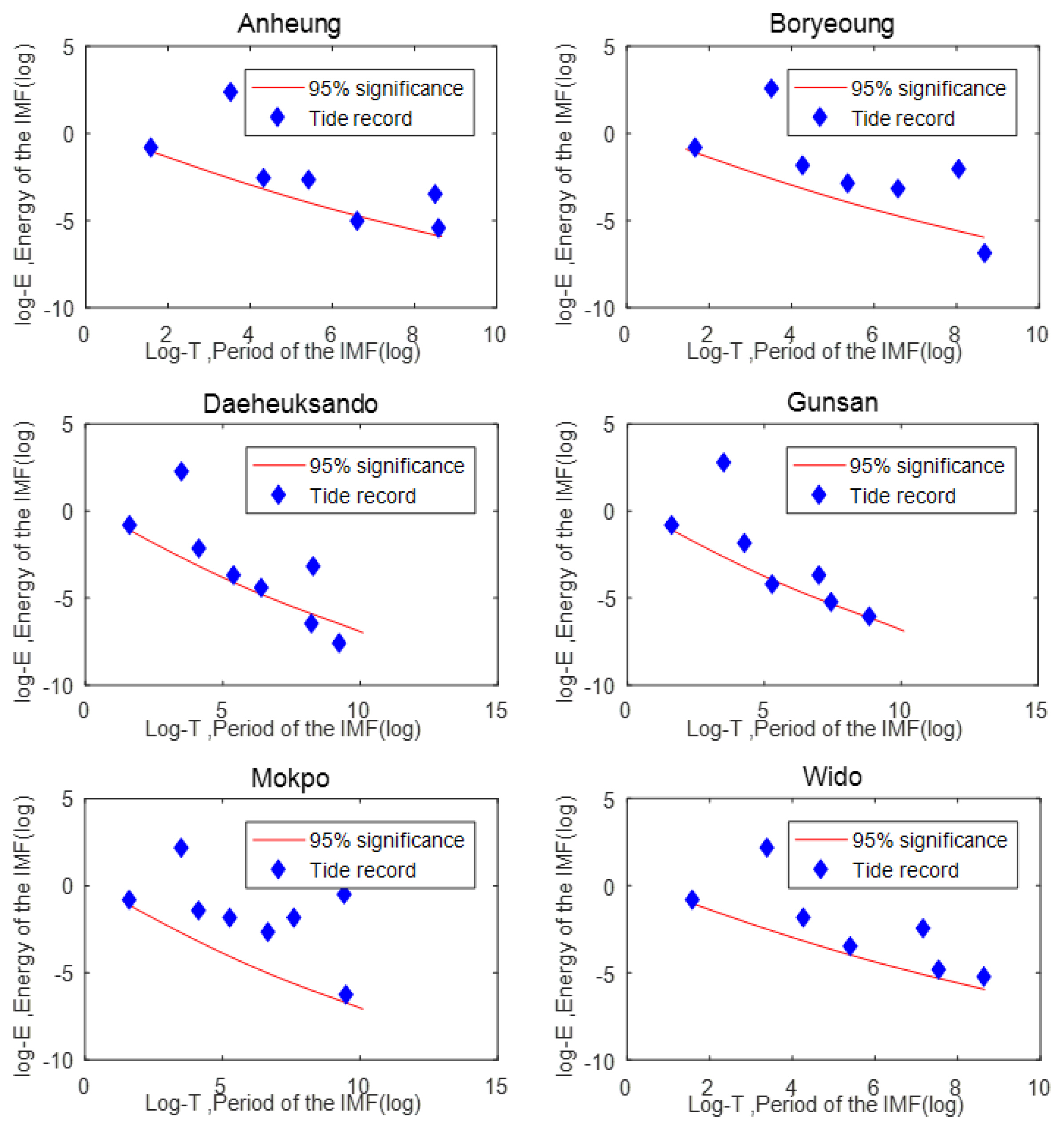
CWT와 EEMD 방법을 통해 분해된 주기 성분들이 실제로 경향성을 분석하기에 유용한 정보인지, 단지 noise인지를 결정하는 유의성 검정(significance test)이 필요하다. CWT 방법에 대한 유의성 검정에는 Monte-Carlo simulation으로 행해지는 Fourier power spectrum과 global wavelet spectrum 기반 통계적 유의성 검정 방법이 있다(Lau and Weng, 1995, Maraun and Kurths, 2004, Torrence and Compo, 1998). EEMD 방법에 대해서는 white noise에 대한 Monte-Carlo 실험을 통한 통계적 유의성 검정이 있다(Wu and Huang, 2004, Wu and Huang, 2009). CWT와 EEMD 방법에서 95% 이상의 신뢰수준을 가진 성분은 통계적으로 유의하다고 간주하였다. Figs. 7 and 8에 CWT와 EEMD 방법의 유의성 검정 결과를 나타내었다. CWT 방법의 경우 각 주기 T(Period)에 해당하는 Global Wavelet Power(GWP) P(Power)를 표시하였으며 Wavelet Spectrum이 신뢰구간 위쪽에 나타나면 해당 주기를 가진 스펙트럼이 통계적으로 유의함을 나타낸다(Kwon and Moon, 2005, Torrence and Compo, 1998). EEMD 방법의 경우 통계적 유의성을 검정하는 기준으로 각 주기 성분에 해당하는 E(Energy of the IMF)를 비교한다(Wu and Huang, 2009). 파란색 점들은 분해된 주기 성분을 나타내며 이 성분들이 95% 신뢰구간인 빨간 선 위에 있으면 통계적으로 유의함을 의미한다.
유의성 분석결과에 따르면 CWT 방법보다 EEMD 방법이 더 신뢰성 높은 결과를 나타내었으며 자료 길이나 경향의 크기에 영향을 받지 않고 더욱 뛰어난 경향성 식별 성능을 보여주었다.
Table 3은 서해안 6개 조석관측지점의 관측조위를 활용한 CWT 및 EEMD 방법을 통한 경향성 분석 및 95% 유의성 검정 결과이다. EEMD 방법 기준으로 해수면 상승 경향 추정 결과, 남해안에 가까운 목포 지점에서 4mm/year의 가장 큰 상승률을 보였으며, 안흥, 보령, 군산의 서해안에 위치한 지점들에서는 2~3mm/year의 상승률을 나타내었다. 해수면 상승 검토 결과 새만금 방조제(군산)의 평균해면은 최대 1.97 mm/year (CWT방법)과 2.51 mm/year (EEMD방법)로 상승하고 있다.
4. 결 론
기후변화에 따른 해수면의 상승이 새만금 방조제에 미치는 영향에 대하여 지난 30년간의 6개 조위관측자료를 기반으로 CWT와 EEMD방법을 활용하여 경향성을 분석하였다.
1) 국립해양조사원의 선형회귀분석방법에 따르면 새만금 방조제(군산)의 평균해면은 최대 2.4 mm/year로 상승하고 있다.
2) CWT 방법을 통한 해수면 상승 검토 결과 새만금 방조제(군산)의 평균해면은 최대 1.97 mm/year로 상승하고 있다.
3) EEMD 방법을 통한 해수면 상승 검토 결과 새만금 방조제(군산)의 평균해면은 최대 2.51 mm/year로 상승하고 있다.
EEMD 방법에 의한 결과가 선형회귀분석 방법보다 최대 0.11mm가량, CWT 방법보다는 0.54mm가량 증가하는 것으로 평가되었다. 이는 경향성을 추출하는 방법론의 차이로서 본 연구에서 적용한 EEMD 기법이 CWT 기법이나 회귀분석을 통한 경향성 분석에 비해 보다 높은 신뢰성을 가진 것으로 판단할 수 있다.
참고로, 새만금 방조제의 여유고는 0.92m이므로 EEMD 방법에 의한 해수면 상승 2.51 mm/year를 고려하면 366년 후에 해수면상승으로 인한 여유고를 초과하므로 향후 오랫동안은 새만금 방조제에서 해수면상승에 의한 영향을 고려할 필요가 없다는 결론이 도출된다. 다만 평균적으로 상승하고 있는 조위에 폭풍해일과 같은 이상기후가 복합적으로 발생하는 경우 위험도 증가할 수 있는 점은 고려할 필요가 있다.







 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print