태풍 마이삭과 하이선에 의한 한반도 폭풍파 수치모의
Numerical Simulation of Storm Waves during Typhoon Maysak and Haishen in the Korean Peninsula
Article information
Trans Abstract
In this study, we simulated storm waves induced by typhoon Maysak and Haishen in the Korean peninsula by using the third-generation numerical wave model SWAN(Simulating WAves Nearshore). We used the sea-surface wind data of KMA(Korea Meteorological Agency)’s operational meteorological model RDAPS(Regional Data Assimilation Prediction System), and JMA(Japan Meteorological Agency)’s weather forecast model JMA-MSM(Meso-Scale Model) as input forcing of the numerical wave model. In addition, the wind field of the tropical cyclone was established with JTWC(Joint Typhoon Warning Center)’s best track data for the storm wave simulation. We used two different source term options, which consider other physics of energy generation by wind and dissipation by whitecapping. Validation of the simulation result was conducted over statistical analysis with the observation data from KMA and KHOA(Korea Hydrographic and Oceanographic Agency)’s buoys. As a result, the whole scenario tended to overestimate significant wave height. The simulation result by using RDAPS as input forcing outperformed the result by using JMA-MSM. It denoted that the performance of a wave model depends on the accuracy of input forcing wind. The wind field by JTWC’s best track data was not suitable compared with the meteorological numerical model. ST6 simulated the wave height higher than Komen’s source term. However, Komen's source term simulated storm waves better than ST6 in this study, and further researches under various conditions are required to evaluate ST6 for the storm waves simulation. In the simulation of wave period parameters, it was hard to estimate the accuracy of the model, and other approaches are necessary for the evaluation.
1. 서 론
한반도에서 발생하는 폭풍파는 겨울철 동해상의 저기압성 바람으로 인해 발생하거나, 매년 내습하는 태풍에 의해 발생한다. 폭풍파는 일반적인 풍파와 비교하여 주기가 길고 파고가 높으며, 연안에 내습할 시 구조물이나 시설에 처오름을 일으켜 피해를 입힌다 (Lee et al., 2020). 특히 태풍에 의해 발생하는 폭풍파는 겨울철에 내습하는 폭풍파에 비해 빈도는 낮지만, 한반도에서 발생할 수 있는 가장 극한의 파랑으로 매년 주기적으로 내습하여 많은 인명 및 재산 피해를 일으킨다. 현재는 기후변화로 인해 한반도에 내습하는 태풍의 강도와 빈도가 점차 증가하여, 이에 동반되는 폭풍파로 인해 발생하는 피해 또한 증가하는 추세이다. 폭풍파로 인해 연안에서 발생할 수 있는 피해를 최소화하기 위해서는 연안 구조물 및 시설에 대한 과학적인 설계 등의 구조적인 해결방안이 필요로 하다. 그리고 폭풍해일, 처오름, 폭풍파의 매개변수(파고, 주기) 등에 대한 신뢰성 있는 예측 등의 시스템적인 해결방안의 중요성도 간과할 수 없다.
시스템적인 해결방안을 개선하기 위해서 한반도 주변 해역에서 폭풍파에 대한 파랑 수치모델의 예측 정확도를 검증하는 다양한 연구가 수행되어왔다. Chun et al. (2014)은 동해에서 폭풍파의 특성을 분석하여 수정된 3세대 파랑 수치모형인 WAM(WAve Model)을 사용해 겨울철에 발생한 폭풍파를 재현하였다. Do and Kim (2018)은 기상청의 현업 기상예보모델인 RDAPS와 WRF(Weather Research and Forecast, Park et al., 2015)의 시공간 바람 자료와 Rogers et al. (2003)에서 제안한 백파에 의한 에너지 감쇠항의 계수조정을 SWAN에 적용하여 동계 폭풍파의 모의 정확도를 향상시켰다. Son and Do (2021)는 관측연구 기반의 원천항인 ST6 (Rogers et al., 2012)를 사용한 동계 폭풍파 수치모의를 통해 SWAN 모델을 동해안에 적용시킬 수 있게 최적화하는 연구를 수행하였다. Kim et al.(2020)과 Kwon et al. (2020)은 JTWC의 Best Track 자료를 활용하여 각각 태풍 볼라벤(Bolaven)과 콩레이(Kong-Rey)에 의해 발생한 폭풍해일과 폭풍파를 수치모의 하였다. Yoon et al. (2020)은 JMA-MSM과 유럽중기기상예보센터(ECMWF; European Center for Medium-range Weather Forecasts)의 최신 재분석자료인 ERA5(ECMWF Re-Analysis 5th Generation), JTWC의 Best Track 자료를 기반으로 구축한 해상풍 자료를 입력 외력으로 하여 1959년 태풍 사라(Sarah) 이후 가장 강력한 태풍인 매미(Maemi)에 의해 발생한 폭풍해일 및 폭풍파를 수치모의 하였다.
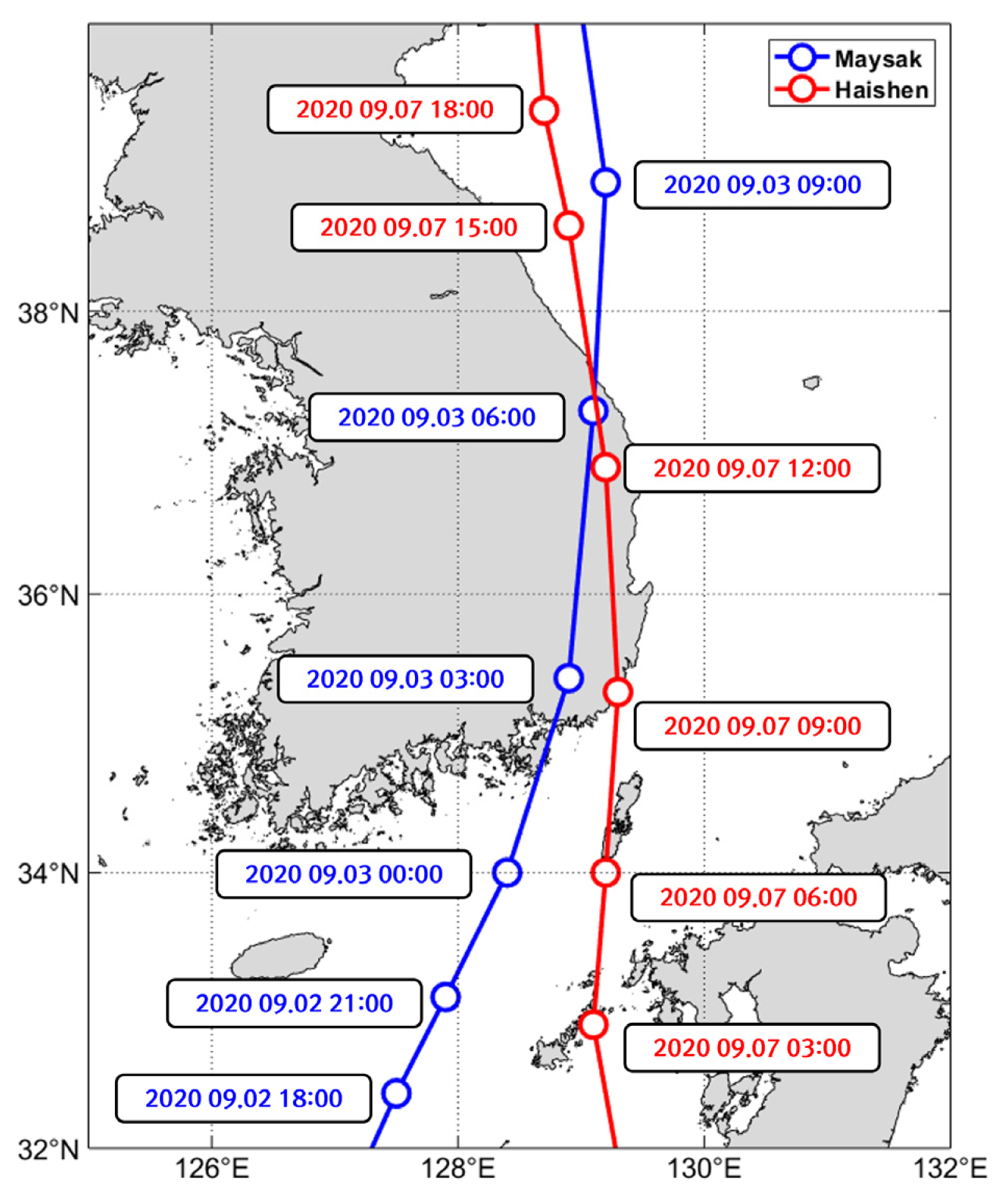
최근 2020년 한반도에 내습한 태풍인 제9호 태풍 마이삭(Maysak)과 10호 태풍 하이선(Haishen)은 각각 필리핀과 괌 인근 해상에서 발생하여 초가을에 동해와 남해 연안, 제주도 및 울릉도 등의 해안지역에서 극심한 인명 및 재산 피해를 유발하였다. Fig. 1에는 마이삭과 하이선이 한반도에 내습하였을 때의 경로와 시간대를 나타내었다. 두 태풍은 약 4~5일 간격을 두고 거의 동시에 내습하였으며, 동해와 남해의 해안 인접 지역에서 인명 및 재산 피해를 유발하였다. 마이삭은 2003년에 발생하여 역대 한반도에 가장 큰 피해를 남긴 태풍 매미(MAEMI)와 비슷한 경로로 진행하여 폭풍해일을 일으키며 연안에 피해를 일으켰다. 마이삭과 하이선의 최대 풍속은 50 ~ 55 m/s 내외를 기록하여, 한반도에서 발생한 역대 태풍 중 손에 꼽을 만한 강한 태풍으로 기록되었다. 본 연구에서는 시스템적인 방안의 일환으로서 파랑 수치모델인 SWAN의 v41.31A를 사용하여 태풍 마이삭과 하이선으로 인해 발생한 폭풍파를 수치 모의하여 파랑 매개변수에 대한 예측 성능을 검증하였다. 수치모델의 입력 외력은 대한민국 기상청의 현업예보모델인 RDAPS와 일본 기상청의 중규모 예보모델인 JMA-MSM의 예보자료에서 취득한 해상풍 자료를 사용하였다. 앞서 언급한 태풍에 의해 발생한 폭풍파를 포함한 대부분의 한반도 주변해역의 파랑 수치모의 연구에서는 JMA-MSM의 바람장이 사용되어왔다. 따라서 본 연구에서는 더욱 정확한 파랑 수치모의를 위해 한반도 주변의 관측자료를 통한 자료동화를 실시하여 정확한 예보자료를 생성한다고 알려진 RDAPS의 바람장을 추가로 입력 외력으로 선정하였다. 파랑 수치모의에 사용한 기상 예보모델의 태풍 시기 바람 자료의 민감도 분석 및 정확도 검증을 위하여, 유럽중기기상예보센터의 ERA5 재분석자료를 이용하였다. 또한 JTWC의 Best Track 자료와 Holland et al. (2010)에서 제안한 기법을 통해 구축한 태풍의 해상풍 바람장을 폭풍파 수치모의에 입력 외력으로 사용하여 모의 결과에 대한 비교 및 분석을 실시하였다. 파랑 수치모의는 SWAN에서 선택할 수 있는 Komen et al. (1984) (이후, Komen으로 표기함) 와 ST6(Rogers et al., 2012)의 서로 다른 원천항을 사용하였다. Son and Do (2021)는 동해에서 발생한 동계 폭풍파 수치 모의 연구에서 ST6를 사용해 과소 추정되는 폭풍파의 유의파고(Hm0)를 조금 더 높게 모의하여 Komen의 원천항보다 관측치에 가깝게 모의하였다. Son et al. (2018)은 일반적인 너울 조건에서 Komen의 원천항이 파랑을 과대 추정하는 문제를 ST6를 사용해 동해 연안의 너울성 파랑의 모의 정확도를 개선하였다. 하지만 한반도 주변 해역에서 태풍에 의해 발생한 폭풍파 수치모의에 ST6의 원천항을 사용한 사례는 제한적이다. 앞서 언급한 태풍 시기(볼라벤, 콩레이 및 매미)에 발생한 폭풍파를 모의한 선행연구에서는 비구조격자체계의 SWAN과 Komen의 원천항을 사용하였다 (Kim et al., 2020; Kwon et al., 2020; Yoon et al., 2020). 해외의 연구사례를 살펴보면, van Vledder et al. (2016)에서 SWAN의 ST6를 사용하였을 때 기존의 Komen et al. (1984)과 Westhuysen (van der Westhuysen et al., 2007)의 원천항보다 북해에서 발생한 폭풍파의 수치 모의 성능이 더 뛰어났다. Liu et al. (2017)에서는 ST6를 사용하여 허리케인 조건에서 발생한 멕시코만의 폭풍파를 성공적으로 모의하였다. 따라서 본 연구에서는 입력 외력 해상풍 자료와 두 가지 다른 원천항인 Komen과 ST6를 토대로 다양한 시나리오 구성하여, 한반도에서의 극한의 기상 조건을 만족하는 태풍 마이삭과 하이선에 의해 발생한 폭풍파를 수치모의 하였다. 이를 토대로 얻어진 결과를 바탕으로 통계 분석 및 검증을 실시하여, 한반도 주변 해역에서 발생한 폭풍파 예측에 대한 ST6의 적용성을 검토하였다.
2. 파랑 수치모델
본 연구에서는 네덜란드 Delft 공대에서 개발한 3세대 파랑 수치모델인 SWAN (Booij et al., 1999)을 사용해 태풍 마이삭과 하이선에 의해 발생한 한반도의 폭풍파를 수치 모의하였다. SWAN의 지배방정식은 파랑 스펙트럼의 형태를 사전에 가정하지 않고 2차원 수평 공간에서 에너지 스펙트럼의 변화를 계산하는 파작용 평형 방정식(wave action balance equation)으로 다음과 같이 식 (1)로 표현된다.
여기서 θ는 파향, σ는 각 주파수로 2π/f로 나타내고, N은 파작용 밀도 스펙트럼으로 파향 에너지 스펙트럼을 주파수로 나눈 N = E(σ,θ)/σ로 표현된다. cx,cy,cθ,cσ는 각 위상 (x,y,θ,σ)에서의 파랑 에너지의 전파속도를 나타낸다. SWAN은 바람에 의한 파랑 에너지의 성장과 굴절(refraction), 천수(shoaling), 반사(reflection) 및 회절(diffraction)에 의한 파랑의 전파를 반영하며, 3파/4파(triad/quadruplet) 비선형작용에 의한 파랑의 변형과 백파현상(whitecapping), 쇄파(breaking), 해저마찰(bottom friction)에 의한 파랑 에너지 감쇠현상을 고려하여 천해와 심해에서 발생하는 파랑을 수치 모의 할 수 있다. 우변의 ST는 바람, 파랑의 비선형작용, 백파현상, 해저마찰, 쇄파 등에 의한 파랑 에너지 밀도(wave energy density)의 생성 및 감쇠를 나타내는 원천항(source term)으로 식 (2)와 같이 표현된다.
여기서 Sin 은 바람에 의한 파랑 에너지의 성장, Snl3과 Snl4는 각각 파랑의 3파 4파 중첩 비선형작용, Sds,w, Sds,b와 Sds,br 각각 백파현상, 해저마찰과 수심에 따른 쇄파로 인한 에너지 감쇠를 의미하는 항이다 (WAMDI Group, 1988). 본 연구에서는 Komen et al. (1984)의 원천항과 관측연구 기반으로 개발된 ST6(Rogers et al., 2012)의 바람에 의한 파랑 에너지의 성장항과 백파에 의한 파랑 에너지의 감쇠항을 폭풍파 수치 모의에 활용하였다.
2.1 Komen et al. (1984)
SWAN의 원천항에서 바람에 의한 파랑 에너지의 성장은 식 (3)과 같이 표현된다.
여기서 A 는 Cavaleri and Rizzoli (1981)의 선형 성장항을 의미하며 식 (4)와 같이 나타낸다. H 는 필터, θw는 풍향 그리고 g는 중력가속도를 나타낸다. BE(σ,θ) 는 지수 성장항을 의미하며, 여기서 B 는 식 (5)와 같이 표현된다 (Komen et al., 1984). 이때 ρa와 ρw는 각각 해수 및 대기의 밀도, Cph는 위상속도, U* 는 바람의 shear velocity로 10m 높이에서의 풍속인 U10 과 바람응력계수 CD에 관한 식으로
백파에 의한 에너지 감쇠는 Hasselmann (1973)의 펄스 기반 모델로 식 (6)과 같이 표현된다 (WAMDI Group, 1988).
여기서 k는 파수를
2.2 ST6 (Rogers et al., 2012)
ST6는 관측연구 기반의 파랑 에너지의 성장과 백파에 의한 파랑 에너지의 감쇠에 관한 연구를 반영하였다. ST6에서 바람에 의한 파랑 에너지의 성장은 식 (8)과 같이 표현된다.
여기서 G는 대기에서 파 발생하는 모멘텀을 조정하는 계수로 식 (9)와 같이 표현되며, Bn은 스펙트럼 포화도, W는 바람으로 인한 파랑 에너지의 성장 및 감쇠(positive and negative)를 담당하는 식이다. ST6에서 풍속은 shear velocity에 대한 식인 US = windscaling × U* 로 표현된다. Liu et al. (2019)는 ST6 원천항을 개선하는 연구에서 windscaling 을 기존의 값인 28에서 32로 수정하였을 때 파랑 에너지 스펙트럼의 tail 영역(특히 High Frequency)의 모의 정확도가 뛰어나다고 언급하여, 현재는 SWAN v.41.31A에서 디폴트 값으로 사용된다.
ST6에서 백파에 인한 파랑 에너지의 감쇠항은 두 가지 위상의 합으로 식 (11)과 같이 표현된다.
여기서 T1은 내부 쇄파항, T2는 누적 쇄파항 이며 각각 식 (12), (13)로 표현된다. ET는 임계밀도 스펙트럼, A는 임계밀도 스펙트럼에 대하여 쇄파 여부를 결정하는 계수, a1과 a2는 각 쇄파항을 조절하는 상수, L과 M은 에너지 감쇠를 조정하는 멱수이다. ST6에 관한 세부적인 사항은 Rogers et al. (2012), Zieger et al. (2015) 및 WAVEWATCH III Development Group (2016)에 명시되어 있으며, SWAN에도 동일하게 적용된다.
3. 모델 구성 및 시나리오
3.1 격자, 수심 및 물리계수
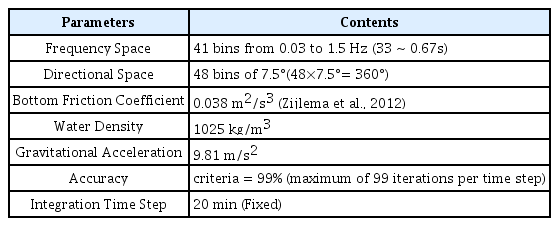
태풍에 의해 발생하는 폭풍파의 성장과 전파, 그리고 소멸을 모의하기 위해 수치모델의 계산영역은 동해와 태풍 경로를 일부 포함하는 대한해협 및 동중국해 전체로 0.04˚×0.04˚해상도 (약 4.5km)의 정방 격자로 구성하였다. Fig. 1에서 나타낸 마이삭과 하이선의 경로를 고려해 서해영역은 수치 모의 영역에서 제외하였다. 수치모델의 수심은 약 15 arc second(약 450m)의 해상도를 가지는 글로벌 수심 데이터 GEBCO(General Bathymetric Chart of the Oceans, https://gebco.net) 2019를 계산 격자에 맞추어 보간하여 사용하였다. Fig. 2에는 파랑 수치모델의 계산영역과 수심 데이터를 각각 (a)와 (b)에 나타내었다. 파랑의 파고와 주기의 매개변수를 정밀하게 모의하기 위해 주파수 분할과 공간분할을 각각 0.03 Hz부터 1.5Hz까지 41개, 공간분할은 7.5°간격으로 48개로 나누었으며, 계산시간은 20분으로 설정하였다. 이와 같은 설정으로 Do and Kim (2018)과 Son and Do (2021) 에서 동계 폭풍파를 성공적으로 모의하였다. 그 외 수치 모의에 필요한 물리 매개변수의 설정은 디폴트 값을 사용하였으며 Table 1에 요약하여 나타내었다.
3.2 입력 외력 해상풍
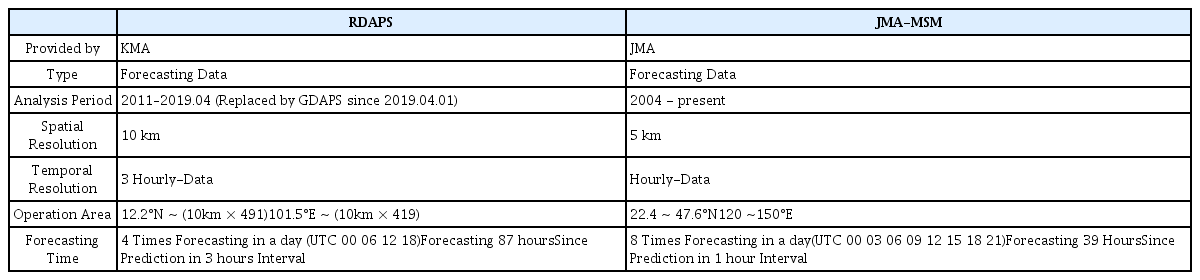
한반도 주변 해역의 파랑 예측 정확도는 입력 외력으로 사용되는 해상풍의 정확도가 큰 영향을 끼치는 것으로 알려져 있다 (Yoon et al., 2020; Kim et al., 2020; Son and Do, 2021). 그렇기에 태풍에 의해 발생하는 폭풍파를 정확하게 모의하기 위해서는 입력 외력 해상풍 자료를 생산하는 기상 수치모델이 바람을 정확하게 예측하여야 한다. 본 연구에서는 한반도 주변을 대상으로 하는 현업 기상 예보모델인 대한민국 기상청의 RDAPS와 일본 기상청의 중규모 예보모델인 JMA-MSM (Saito et al., 2006)의 해상풍 자료를 폭풍파 수치 모의의 입력 외력으로 사용하였다. 두 기상 수치 예보모델 모두 4차원 변분자료동화기법(4D-VAR data assimilation system)을 사용하여 정확도가 매우 높다고 알려져 있으며, 한반도 주벽 해역의 파랑 수치 모의 연구에 사용되어왔다. RDAPS는 GDAPS(Global Data Assimilation and Prediction System)로부터 경계조건을 받아 1일 4회 (UTC 00 06 12 18) 예측을 실시하여 3시간 간격의 87시간의 단기 예측자료를 생산한다. 하지만 2019년 4월 1일부터 RDAPS의 자료 생산 중단으로 GDAPS의 지역 영역자료로 대체되어, 단일면 자료의 공간해상도가 12km에서 10km로 개선되었다. JMA-MSM은 1일 8회 (UTC 00 03 06 09 12 15 18 21) 예측을 실시하여, 1시간 간격의 39시간 단기 예측자료를 생산한다. 본 연구에서는 각 예측 시간에 생산한 단기예측자료를 활용하여, 각 3시간 및 1시간 간격의 해상풍 자료를 구성하여 파랑 수치 모의에 활용하였다. 유럽중기기상예보센터의 재분석자료인 ERA5 (Hersbach et al., 2020)는 매우 정확한 바람 자료를 가지고 있지만, 상대적으로 낮은 공간해상도를 가지며 선행 연구에서 폭풍파 수치 모의에서 파고를 낮게 재현하는 경향이 있다는 것을 확인하였다 (Yoon et al., 2020; Kwon et al., 2020; Son and Do., 2021). 따라서 ERA5는 본 연구에서 폭풍파 수치모의의 입력 외력으로 적합하지 않다고 판단하여 해상풍 자료의 정확도 분석에만 활용하였다. Table 2에는 본 연구에서 파랑 수치모의 입력 외력으로 사용한 기상 예보모델의 정보를 요약해서 나타내었다.
본 연구에서는 JTWC Best Track 데이터와 Holland et al. (2010)의 기법을 사용한 모델로 열대 저기압 해상풍 자료를 구축하여 폭풍파 수치모의에 활용하였다. 이는 한반도 주변을 대상으로 하는 두 기상 예보모델의 태풍 시기 바람의 예측 정확도와 파랑 수치모델의 입력 외력으로서의 적합성을 검증하기 위한 것이다. Best Track 자료는 태풍이 발생한 후에 재분석을 통해 만들어진 태풍 정보이며, 본 연구에서는 JTWC의 Best Track 자료의 태풍 경로, 시간(UTC 00 06 12 18), 최대풍속, 중심기압, 최대풍속반경, 4분할(NE, SE, SW, NW; 1st ~ 4th quadrant)로 제공되는 각 풍속(35, 50, 65, 100 knot)의 반경 데이터를 해상풍 자료 구축에 이용하였다. 여기서 최대풍속과 중심기압의 관계식 및 최대풍속반경과 기압차의 관계식은 각각 Holland (2008), Gross et al. (2004)의 관계식을 사용하였다. JTWC의 Best Track 자료기반의 해상풍 자료는 DelftDashBoard v02.03 (https://publicwiki.deltares.nl/)을 통해 SpiderWebGrid 형식으로 구축하였으며, SWAN의 입력 외력으로 사용할 수 있게 변형하는 과정을 수행하였다.
3.3 수치모의 시나리오
수치 모의 기간은 태풍 마이삭과 하이선이 한반도에 내습한 시기를 포함하는 2020년 8월 27일부터 9월 13일로 선정하였다. 해당 기간의 파랑 특성을 분석하기 위해 유럽중기 기상예보센터의 재분석자료인 ERA5의 15년치 (2006-2019년) 데이터를 활용하였다. Fig. 3에는 ERA5 재분석자료의 한 정점(129.78°E 36.35°N)에서 15년 동안 발생한 유의파고와 첨두주기(Tp)를 산점도 그래프로 나타낸 것으로, 붉은색 점은 마이삭과 하이선의 내습 시기에 발생한 유의파고가 높은 순의 상위 20개 이벤트를 나타낸 것이다. 여기서 s는 유의파고와 파장의 비로 표현되는 파랑의 경사도이다. 이를 살펴보면 해당 정점은 통상적으로 유의파고 약 0.5 ~ 1.5m, 첨두주기 약 4 ~ 6초 사이의 파랑이 지배적인 환경이다. 여기서 붉은색 점이 그래프에서 위치하는 분포를 보아 태풍이 내습하였을 때 발생한 파랑은 매우 가파른 장주기성 고파랑인 것을 확인할 수 있다. 또한 점들이 대부분 그래프의 오른쪽 상단에 위치하는 것으로 보아, 마이삭과 하이선에 의해 발생한 폭풍파는 분석 기간 내에 발생한 이벤트 중에서 빈도수가 최소에 가까운 극한조건의 파랑으로 판단된다.
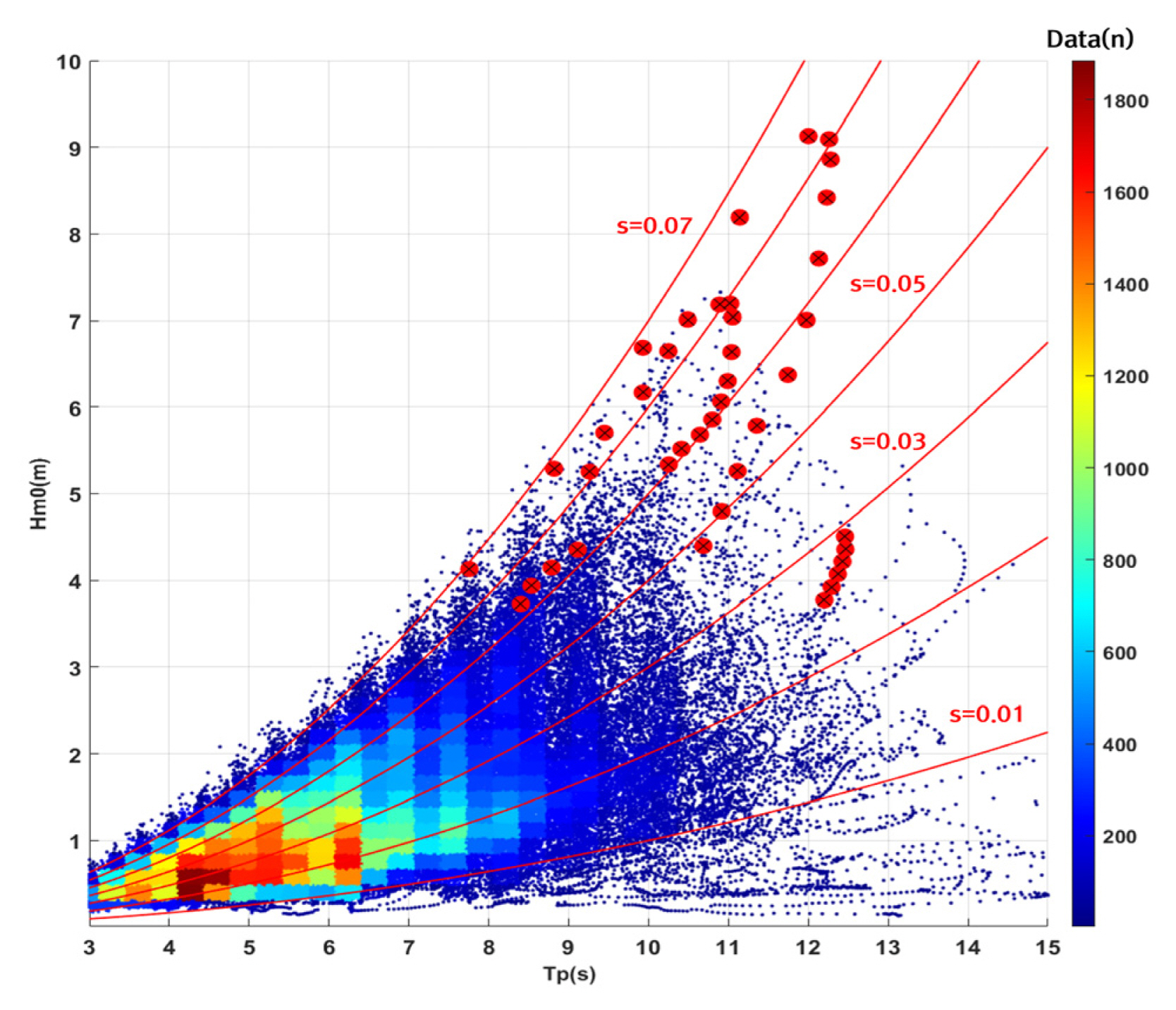
Density scatters of local Hm0 and Tp for 15 years (2006–2020), and circles with red color that indicate 40 incidents recorded during Maysak and Haishen (The data was derived from Re-analysis data of ERA5)
본 연구에서는 RDAPS 및 JMA-MSM 기상 예보모델과 JTWC Best Track 자료 및 Holland et al.(2010)의 기법으로 구축한 해상풍 자료를 폭풍파 수치모의 입력 외력으로 사용하였다. 파랑 수치 모의 원천항은 Komen과 ST6의 서로 다른 바람으로 인한 파랑 에너지 성장과 백파로 인한 파랑에너지 감쇠항을 사용하였다. 이를 입력 외력과 사용한 원천항으로 구분하여 RDAPS-Komen, RDAPS-ST6, JMA-Komen, JMA-ST6, Holland-Komen, Holland-ST6로 표기하기로 한다. Table 3에는 앞서 식 (3)-(13)에 적용되는 파랑 수치모의 원천항의 계수 값을 요약하여 나타내었다.
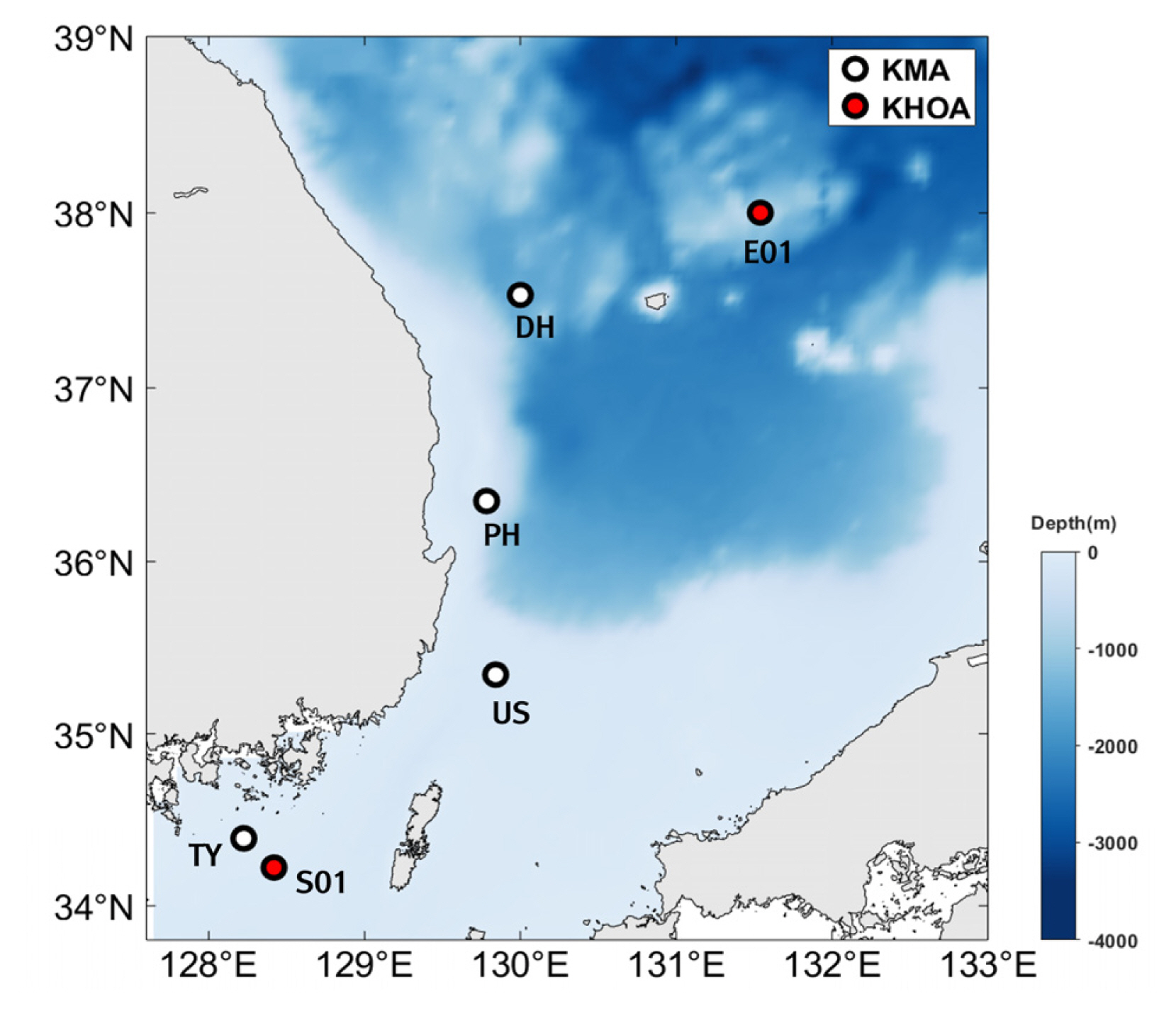
수치 모의 결과 검증을 위해서 동해와 남해에 걸쳐 총 6개 정점의 외해 관측부이 자료를 수집하였다. Fig. 4에는 각 데이터의 관측정점과 수심을 지도에 나타내었다. 결과 검증을 위한 관측치로 국립해양조사원(KHOA)의 해양관측부이(E01, S01)와 기상청(KMA)의 관측부이(DH, PH, US, TY)에서 제공하는 풍속, 풍향, 파고 및 주기를 사용하였다. 수치 모의 결과를 정밀하게 검증하기 위해 파고 및 주기의 관측치는 전국파랑관측자료 제공시스템 WINK(Wave Information Network of Korea) (Jeong et al., 2018)에서 품질 검증을 거친 자료를 활용하였다.
수치모의 결과의 정량적 분석을 위해서 1시간 간격으로 얻은 파랑 수치모의 결과와 앞서 수집한 관측치 간의 통계분석을 실시하였다. 이를 위해 편향오차(MBE, Mean Bias Error), 결정계수(R2, Determinant Coefficient) 및 평균제곱근오차(RMSE, Root-Mean Square Error)를 모델 평가항목으로 선정하였으며, 식 (14)-(16)에 나타내었다. 여기서 n은 관측자료의 개수, M은 모델의 결과값, O는 관측치,
4. 모의 결과 및 검증
4.1 입력 외력 해상풍 검증
본 연구에서는 파랑 수치모델의 입력 외력으로 대한민국 기상청의 RDAPS와 일본 기상청의 JMA-MSM의 해상풍 자료를 이용하였다. 먼저 서로 다른 입력 외력에 따른 파랑 수치모의 결과를 분석하기 위해, 외해 6개의 정점에서 관측된 풍속 및 풍향 데이터를 사용하여 기상 수치모델의 정확도 검증을 실시하였다. Fig. 5에는 각 정점에서 관측된 풍속과 RDAPS, JMA-MSM 및 ERA5의 풍속을 시계열로 나타내었고, Fig. 6에는 풍속 및 풍향의 RMSE를 계산하여 바 그래프로 나타내었다. 이를 분석해보면 RDAPS와 JMA-MSM는 태풍 시기(마이삭; 9/2 ~ 9/4, 하이선; 9/7 ~ 9/8)의 풍속을 과대 추정하였다. 특히, JMA-MSM가 RDAPS와 비교하여 풍속을 더 심하게 과대추정 하였으며, Fig. 6a의 풍속의 RMSE를 비교하였을 때 더욱 눈에 띄게 나타났다. RDAPS와 ERA5의 RMSE의 차이는 약 0.5m/s 내외로 ERA5가 작았고, JMA-MSM과 ERA5의 차이는 약 1 ~ 1.2m/s의 차이를 보인다. 결과적으로 RDAPS는 재분석자료인 ERA5와 비교하였을 때 풍속 예측 정확도가 우수한 것으로 나타났으며, 이는 RDAPS와 GDAPS가 한반도 주변의 관측자료를 사용하여 자료동화를 실시하기 때문으로 판단된다. 풍향의 경우는 세 가지 모델 모두 비슷한 RMSE 값을 나타내었다 (Fig. 6b).
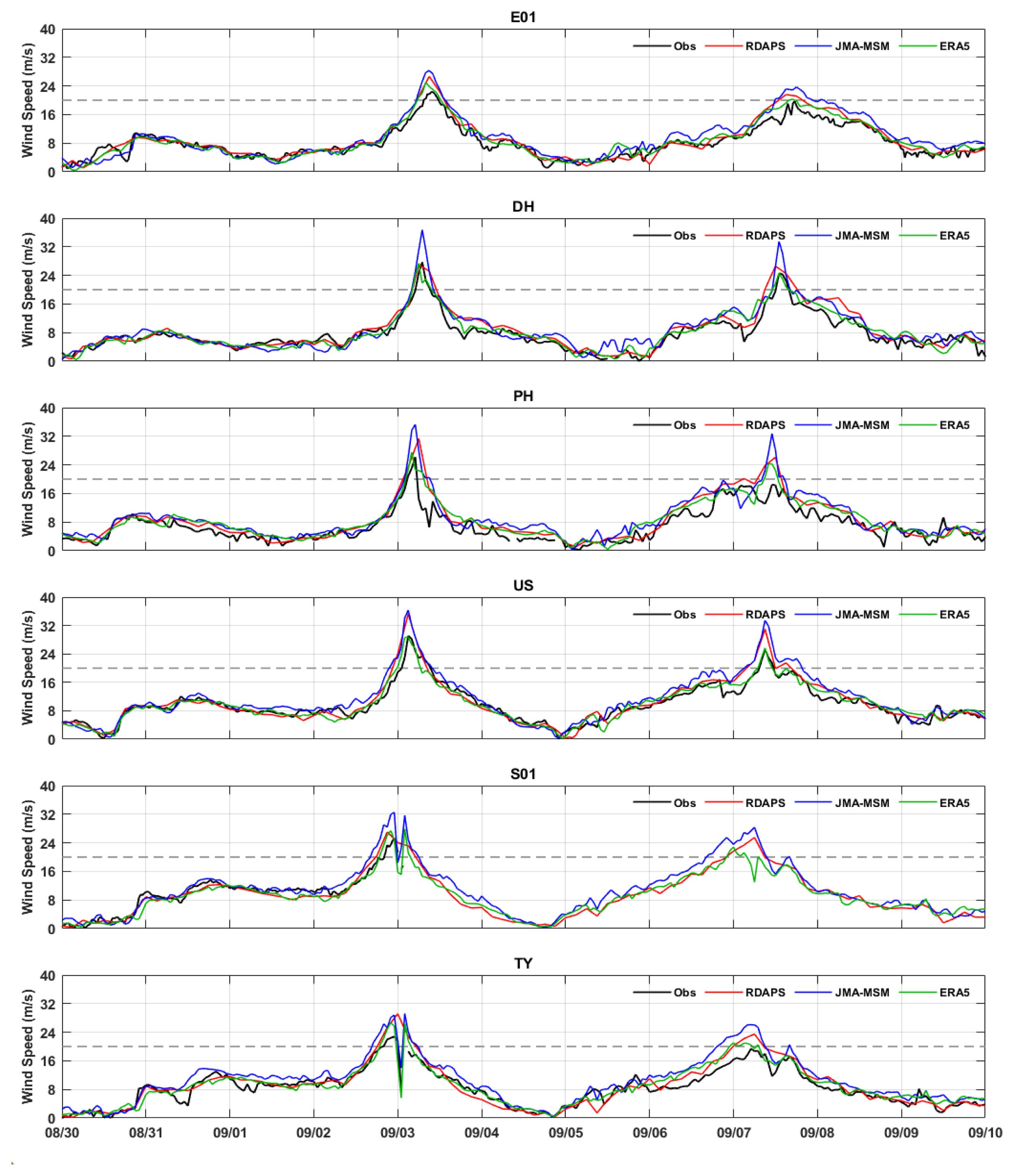
Time series of wind speed from observation buoys and each meteorological model(RDAPS, JMA-MSM, ERA5) at 6 locations. (2020.08.30 – 2020.09.10)
기상 예보모델의 태풍 시기의 바람 예측 정확도와 그에 따른 파랑 수치모의 결과를 비교 및 검증하기 위해 JTWC의 Best Track 자료와 Holland et al.(2010)에서 제안한 기법을 사용하여 열대 저기압 해상풍 바람장을 구축하였다. 해상풍 자료의 정확도를 평가하기 위해 Fig. 7에 JTWC의 Best Track 자료기반으로 구축한 바람장(이후 JTWC-Holland로 표기한다)의 풍속과 기상 예보모델의 풍속 자료 및 관측치를 시계열로 나타내었다. 이를 분석해보면, JTWC-Holland는 마이삭 내습 시기(9/2 ~ 9/4)의 풍속을 JMA-MSM과 매우 유사하게 재현하였다. 하지만 태풍 하이선 내습 시기(9/7 ~ 9/8)에는 남해에 위치한 S01, TY 정점을 제외한 4개의 정점(E01, DH, PH, US)에서 풍속을 과대 추정하였으며, 상대적으로 마이삭에 비해 재현 정확도가 떨어졌다. 또한 Holland 모델은 태풍 중심에서 멀어진 곳의 바람을 모의하지 못한다는 단점이 있어, JTWC-Holland는 6개의 정점에서 태풍이 지나가는 시기에만 풍속의 데이터가 존재한다.
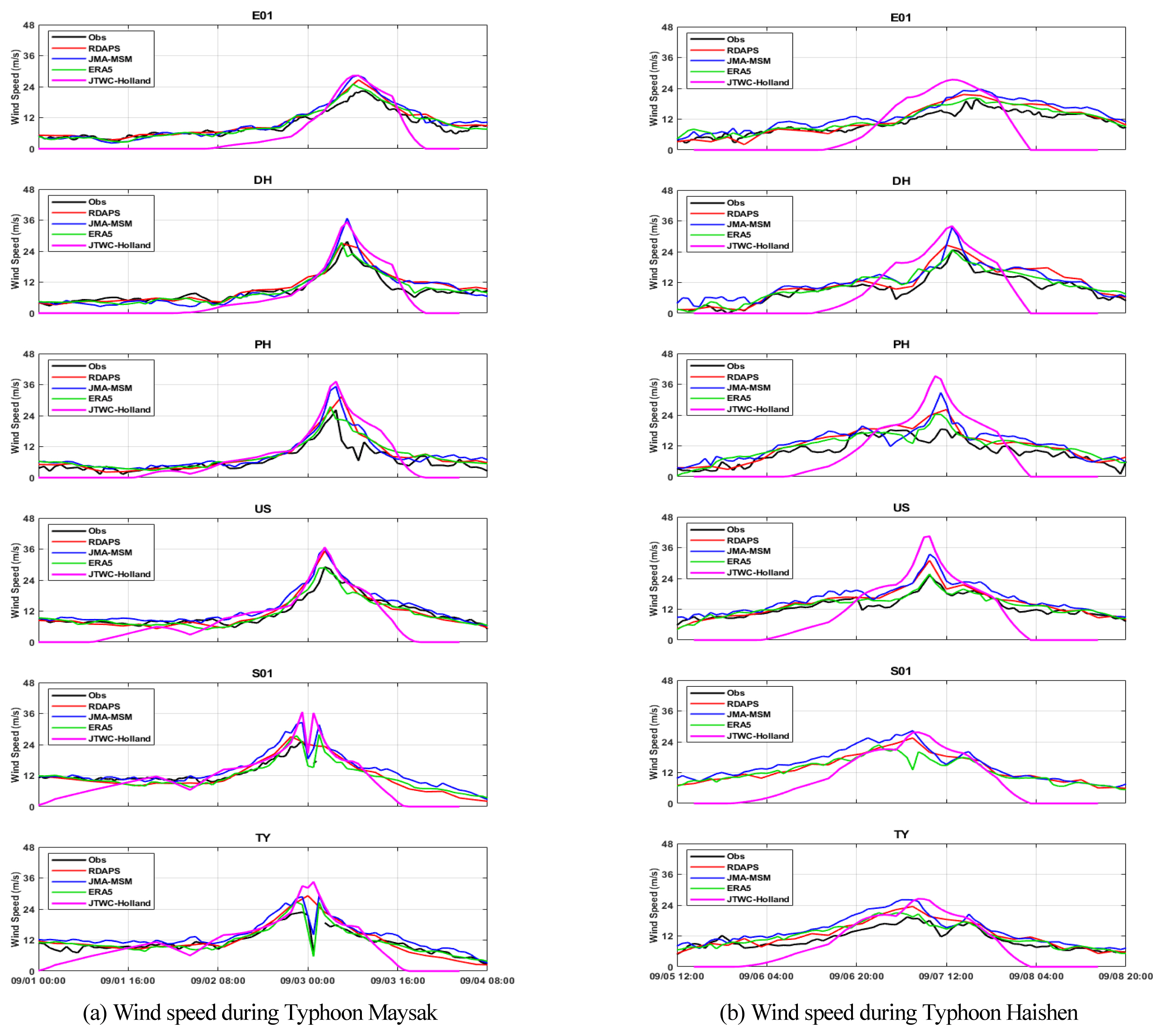
Time series of wind speed from JTWC-Holland, observation buoys, and the other meteorological models at 6 locations during Maysak and Haishen
요약하자면 대한민국 기상청의 RDAPS와 일본 기상청의 JMA-MSM는 태풍 시기에 풍속을 전체적으로 과대 추정하며, 이러한 경향은 JMA-MSM에서 더 크게 나타났다. 기상청의 기상 예보모델인 RDAPS는 관측결과와 모델의 예측 결과를 사용하여 후 처리된 재분석자료인 ERA5의 풍속과 비교하였을 때 RMSE 값의 차이가 크지 않아, 태풍 시기의 풍속 예측에서 상당히 뛰어난 성능을 보여주었다. 또한 JMA-MSM에 비해 더 적은 예측 횟수와 큰 시간 간격에도 불구하고(상대적으로 더 낮은 시공간 해상도를 가짐)에도 불구하고, 한반도 지역에서 태풍 시기에 풍속을 더 정확하게 예측하였다. JTWC-Holland는 태풍 시기의 풍속을 어느 정도 잘 재현하였지만, 마이삭에 비해 하이선 시기의 해상풍 재현 정확도가 상대적으로 떨어졌다. 이는 Best Track 자료의 생성 및 후처리 과정에서 발생할 수 있는 오차 등에 따라 재현된 해상풍의 차이가 있을 수 있다는 사실에 기인하는 것으로 추정된다. 또한 Holland 모델 특성상 제한된 시간에서 국지적인 해상풍 자료의 생성만 가능하다는 한계가 있었다.
4.2 파랑 수치모의 결과
본 연구에서는 RDAPS, JMA-MSM 및 JTWC-Holland의 해상풍 자료를 입력 외력으로 하여, Komen과 ST6의 원천항을 사용해 태풍 마이삭과 하이선에 의해 한반도에서 발생한 폭풍파를 수치모의 하였다. Fig. 8에는 6개의 정점에서의 각 시나리오별 유의파고 수치 모의 결과를 관측치와 함께 시계열로 나타내었다. 이를 분석해보면 전체적으로 파랑 수치모델이 유의파고를 과대 추정하였으며, 태풍 하이선 내습 시기(9/7 ~ 9/8)에 이러한 경향이 더 크게 나타난다. 이와 같은 모의 결과는 기상 예보모델이 태풍 시기에 풍속을 과대 추정하기 때문으로 추정된다. 특히, 입력 외력의 비교 및 검증 결과를 분석하면 JMA-MSM 기상 예보모델이 RDAPS 결과에 비해 상대적으로 풍속을 크게 추정하였다. 이로 인하여, RDAPS의 해상풍 자료를 사용한 수치 모의 시나리오(RDAPS-Komen, RDAPS-ST6)보다 JMA-MSM의 자료를 사용한 수치 모의 시나리오(JMA-Komen, JMA-ST6)에서 폭풍파의 유의파고를 더 크게 과대 추정하고 있으며, 특히 JMA-ST6 시나리오는 관측치와 비교하여 유의파고를 약 3m 내외로 더 높게 과대 추정하였다.
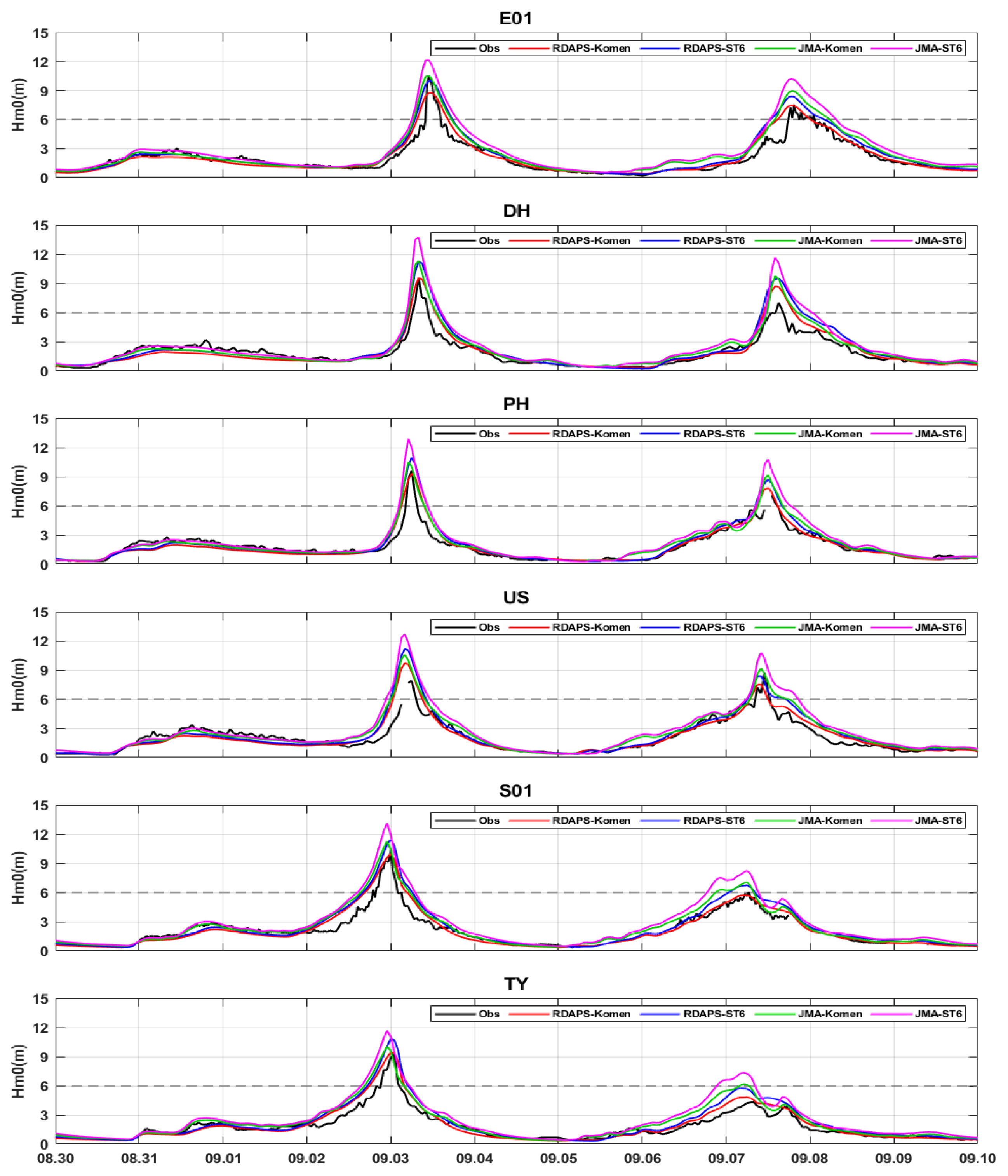
Time series of significant wave height(Hm0) from simulation (RDAPS-Komen, RDAPS-ST6, JMA-Komen, JMA-ST6) results and observation at 6 locations (2020.08.30 – 2020.09.10).
서로 다른 원천항을 사용한 유의파고 수치 모의 결과를 비교하였을 때, ST6를 사용한 수치 모의 시나리오(RDAPSST6, JMA-ST6)가 Komen의 원천항을 사용한 시나리오(RDAPSKomen, JMA-Komen)보다 유의파고를 더 높게 모의하였다. 이를 분석하기 위해 Fig. 9에 파랑 수치모의 과정에서 원천항을 통해 계산되는 파랑 에너지의 총량을 시계열로 6개의 정점별로 나타내었다. 여기서 y축은 파랑 에너지의 총량을 나타내며, 바람으로 인해 증가하는 파랑 에너지(S≥ n; Source term of energy generation)에서 백파현상 등에 의해 감쇠되는 파랑 에너지(Sds; Source term of energy dissipation)를 뺀 값을 나타낸다. 이는 파랑 에너지 평형 방정식에서 계산되는 파랑 에너지 스펙트럼을 전체 주파수와 공간에 대해 적분한 값으로 W/m2의 단위를 가진다. 이를 살펴보면 통상적인 파랑 조건(관측 유의파고가 약 3m 이하인 기간)에서는 Komen과 ST6의 수치모의에서 큰 차이를 보이지 않는다. 하지만 태풍 시기에 급격하게 유의파고가 높아진 파랑을 모의할 때, ST6를 사용한 수치 모의 시나리오(RDAPS-ST6, JMA-ST6)에서 파랑 에너지가 더 민감하게 반응하였다 (마이삭과 하이선의 내습시기인 9/3과 9/7에서 ST6를 사용한 수치모의 시나리오의 파랑 에너지가 더 높게 나타남). 이와 같이 장주기성 고파랑의 폭풍파 수치 모의에서 ST6는 전체적으로 감쇠되는 파랑 에너지를 줄일 수 있어, 유의파고를 더 높게 모의할 수 있는 것으로 추정된다. 이를 종합하면 폭풍파의 유의파고를 과소 추정할 때는 ST6의 원천항을 사용하는 것이 고파랑 모의에 가장 적합하며, 반대로 과대 추정하는 경우에는 Komen의 원천항이 더 적합하다고 판단된다. 본 연구에서는 태풍 시 풍속의 과대 추정으로 인해 파고를 더 낮게 모의한 Komen의 원천항이 폭풍파의 유의파고를 가장 정확하게 모의하였다. SWAN이 기존의 장주기성 고파랑의 성질을 가지는 폭풍파 수치모의에서 유의파고를 과소 추정하는 경향이 있는 것으로 보아 (Do and Kim, 2018; Son and Do, 2021), 정확한 기상 예측 모델을 입력 외력으로 사용하는 최적의 시나리오에서는 ST6의 원천항이 장주기성 고파랑의 수치 모의에 더 적합할 수 있다고 판단된다.
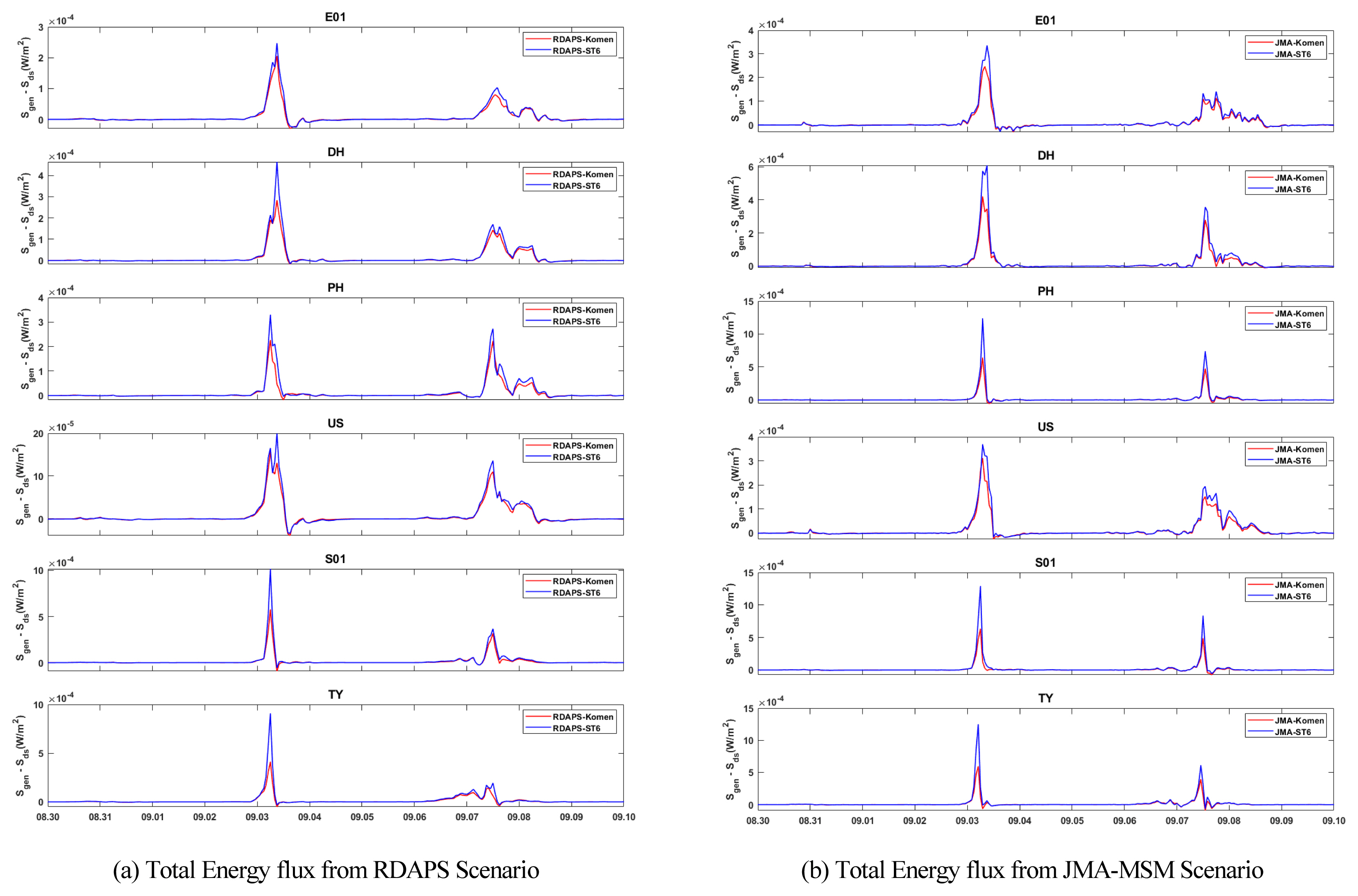
Total energy flux expressed as Sgen(wave energy generation by wind; S∈) - Sds(wave energy dissipation by whitecapping; Sds,w, and swell dissipation; Sds,swell)
Fig. 10에는 유의파고 수치모의 결과를 정량적으로 분석하기 위해 수행한 통계분석 결과를 바 그래프로 나타내었다. 이를 살펴보면 수치모의 결과의 R2은 전체적으로 0.8 이상의 값을 가지며 양호하였다. 앞서 설명한 바와 같이 모델이 유의파고를 전체적으로 과대 추정하고 있어, MBE는 거의 모두 음수 값을 나타냈다. 서로 다른 입력 외력을 사용한 모의 결과에서는 RDAPS의 해상풍 자료를 사용한 시나리오(RDAPS-Komen, RDAPS-ST6)가 JMA-MSM의 자료를 사용한 시나리오(JMA-Komen, JMA-ST6)에 비해 더 낮은 RMSE와 0에 가까운 MBE 값을 나타냈다. 이는 RDAPS가 JMA-MSM보다 태풍 시기의 풍속을 더 정확하게 모의하였기 때문으로 추정되며, 유의파고의 수치 모의에서는 입력 외력으로 사용한 해상풍 자료의 정확도가 매우 중요하다고 판단된다. 서로 다른 원천항을 사용한 모의 결과의 통계치를 살펴보면 Komen의 원천항을 사용한 시나리오(RDAPSKomen, JMA-Komen)가 ST6를 사용한 시나리오(RDAPS-ST6, JMA-ST6)에 비해 더 낮은 RMSE와 0에 가까운 MBE 값을 나타냈다. 앞선 결과에서 입력 외력으로 사용한 해상풍 자료가 태풍 풍속 과대 추정하여 전체 파랑 수치모의 시나리오에서 유의파고를 과대 추정하였다. 따라서 파고를 가장 낮게 모의한 Komen의 원천항을 사용한 시나리오의 통계분석에서 상대적으로 좋은 결과를 얻을 수 있었다고 판단하였다. 결과적으로, RDAPS-Komen의 시나리오에서 MBE값이 0에 가까웠으며, RMSE 또한 가장 낮게 나타나 유의파고를 가장 정확하게 모의하였다.
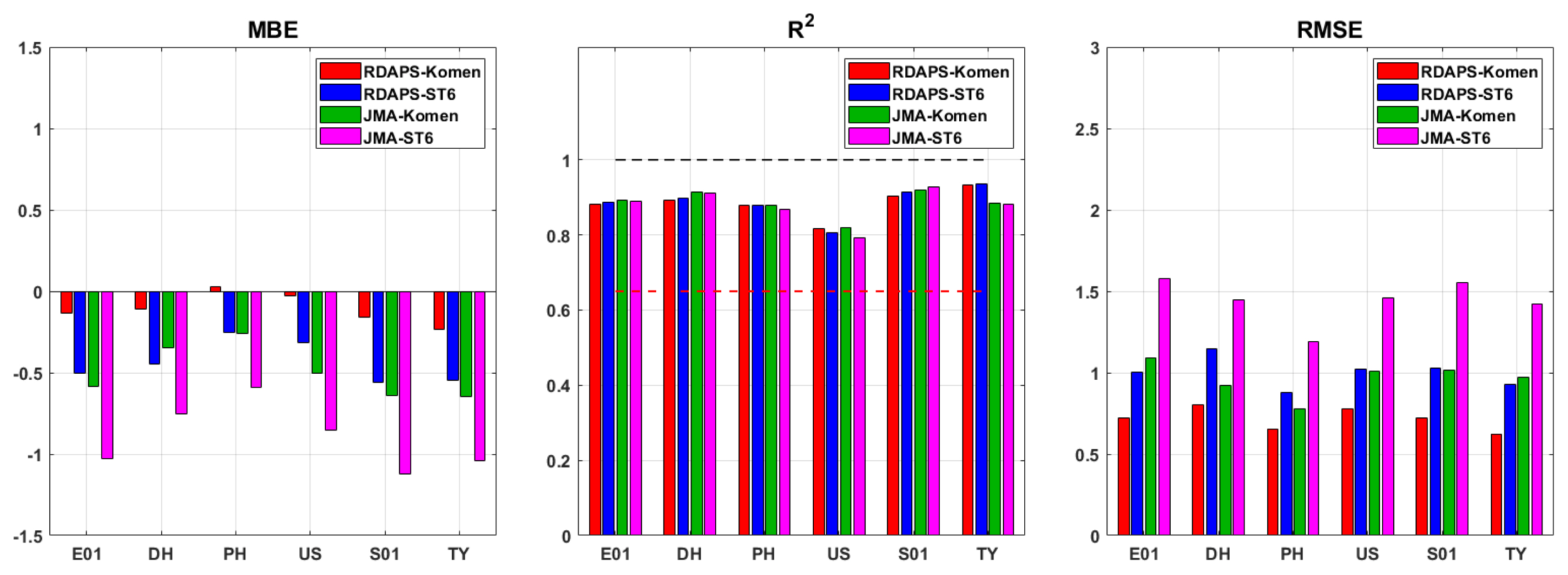
The bar graphs of statistical analysis values(MBE, R2, RMSE) of significant wave height(Hm0) simulation at 6 locations
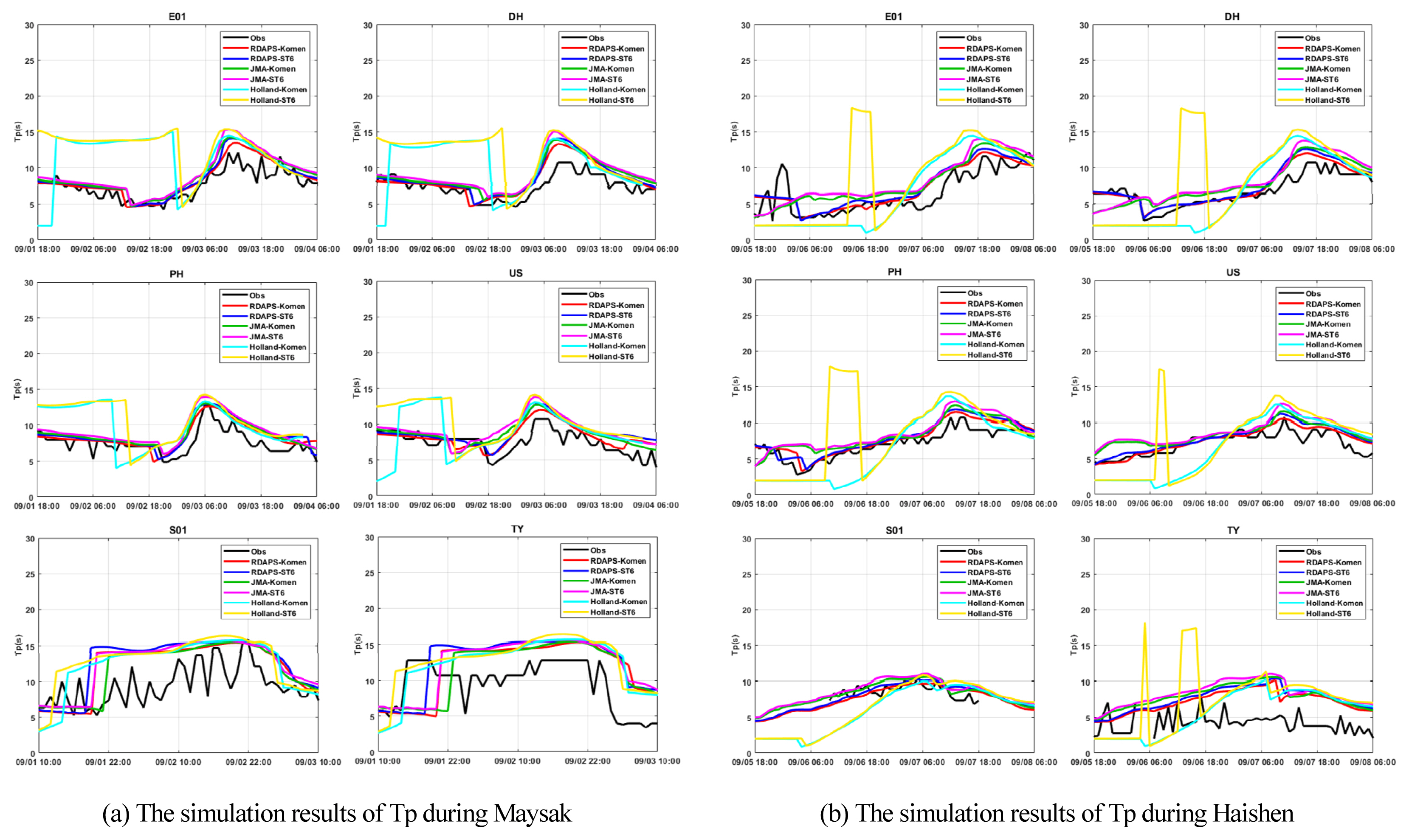
Fig. 11. 에는 JTWC-Holland 해상풍 자료를 사용한 파랑의 유의파고 모의결과를 시계열로 나타내었다. 태풍 마이삭 내습 시기에서는 JTWC-Holland를 사용한 유의파고 모의 결과는 JMA-MSM의 해상풍 자료를 사용한 시나리오(JMA-Komen, JMA-ST6)와 매우 유사한 결과를 나타내었다(Fig 12a). 이는 JTWC-Holland가 태풍 마이선의 풍속을 JMA-MSM 기상모델의 예측 결과와 거의 비슷하게 재현하였기 때문으로 추정된다. 태풍 하이선에 의해 발생한 폭풍파의 유의파고 모의 결과는 앞서 실시한 입력 외력의 정확도 검증에서 살펴본 JTWC-Holland의 풍속과 유사한 결과를 나타내었다. 이는 JTWC-Holland가 4곳의 정점(E01, DH, PH, US)에서 태풍 하이선의 풍속을 과대 추정하는 경향을 나타내었기에, 유의파고의 수치모의 결과에서 비슷한 결과가 나타난 걸로 추정된다.
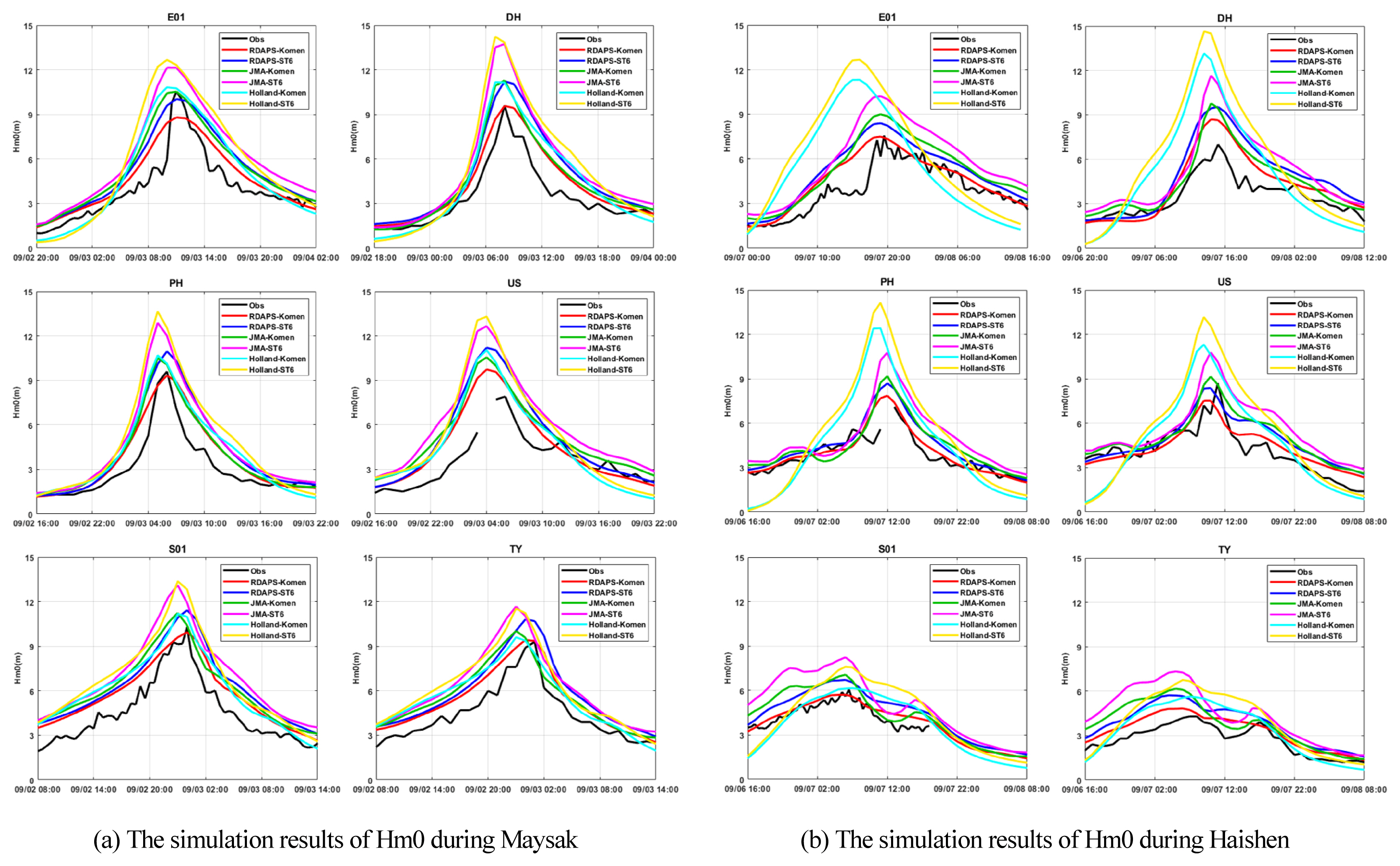
Time series of significant wave height(Hm0) from simulation (RDAPS-Komen, RDAPS-ST6, JMA-Komen, JMA-ST6, Holland-Komen, Holland-ST6) results and observation at 6 locations during Maysak and Haishen
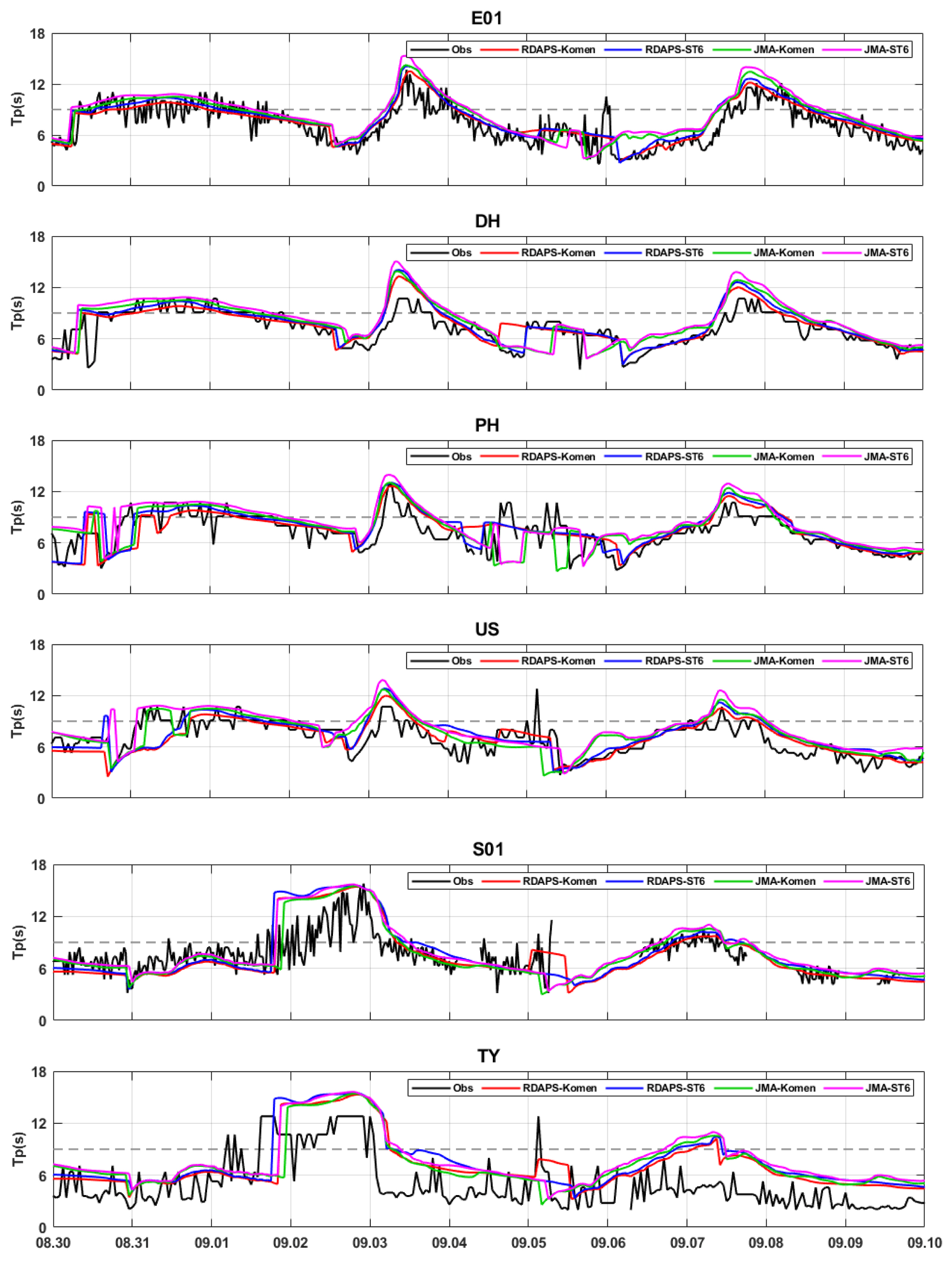
Time series of peak wave period(Tp) from simulation (RDAPS-Komen, RDAPS-ST6, JMA-Komen, JMA-ST6) results and observation at 6 locations (2020.08.30 – 2020.09.10)
폭풍파의 주기 성분에 대한 파랑 수치모델의 모의 정확도를 분석하기 위해 Fig. 12에 6개의 정점에서의 첨두주기 모의 결과를 관측치와 함께 시계열로 나타내었다. 또한 예측 정확도를 정량적으로 분석하기 위해 첨두주기 모의결과에 대한 통계 분석결과를 바 그래프로 Fig. 13에 나타내었다. 먼저 시계열 자료를 살펴보면 모의결과의 트렌드가 관측치를 따라가는 것으로 보이나, 시간적으로 변동성이 크며 불 규칙한 패턴을 보이는 첨두주기 관측치를 정확하게 모의하지 못하였다. 이는 외해에서의 첨두주기 관측에서 발생하는 관측오차의 한계로 인한 것으로 판단된다. 특히, 남해에 위치한 두 정점(S01, TY)에서 첨두주기의 모의 정확도가 상대적으로 매우 떨어졌다. Fig. 13의 통계분석 결과를 살펴보면 RMSE가 가장 낮고 MBE가 0에 가까운 RDAPS-Komen이 가장 좋은 모의결과를 낸 것처럼 보이지만 R2의 값이 DH 정점을 제외한 모든 시나리오에서 0.65보다 낮은 값을 보인다. 결과적으로 외해에서 발생하는 관측자료의 한계로 인해 각 시나리오의 첨두주기 모의 정확도를 비교 및 검증하는 것이 쉽지 않다. Do and Kim (2017)에서도 관측치의 시간적 변동성이 크게 나타난 외해 정점에서의 첨두주기 수치 모의 결과가, 상대적으로 안정적인 관측치를 보여주는 연안 정점에 비해 매우 떨어지는 결과를 나타내었다. 따라서 태풍으로 인해 발생한 첨두주기 성분의 모의 정확도를 평가하기 위해서는, 외해 파랑 주기성분의 관측자료의 품질 관리와 연안 정점에서의 수치모델 평가를 통한 추가적인 연구가 필요하다고 판단된다.

The bar graphs of statistical analysis values(MBE, R2, RMSE) of peak wave period(Tp) simulation at 6 locations
Fig. 14에는 JTWC-Holland 해상풍 자료를 입력 외력으로 사용한 각 외해 정점의 파랑의 첨두주기 모의 결과를 시계열로 나타내었다. 이를 살펴보면 태풍 마이삭 시기에 폭풍파가 발생한 시기인 9월 2일에서 4일 기간에는 전체적으로 기상 수치모델을 입력 외력으로 사용한 파랑 수치모의 결과와 비슷한 결과를 나타내었다. 하지만 4곳의 정점(E01, DH, PH, US)에서 폭풍파 발생 이전 시기인 9월 1일의 첨두 주기를 과대 추정하였다. 하이선의 경우 태풍이 정점에 내습하기 전으로 추정되는 시기인 9월 7일 이전의 모든 정점에서 첨두주기를 과소 추정하고 있으며, Holland-ST6의 경우에는 9월 6시에서 18시경의 5곳(E01, DH, PH, US, TY)의 정점에서 첨두주기를 지나치게 과대 추정하였다. 폭풍파가 발생한 걸로 추정되는 9월 7일 이후의 첨두주기 모의결과는 다른 4가지 시나리오(RDAPS-Komen, RDAPS-ST6, JMAKomen, JMA-ST6)와 유사한 결과를 보여주었다. 하지만 앞선 Fig. 14b의 유의파고 모의 결과와 동일하게 4곳의 정점(E01, DH, PH, US)에서 수치모델 기반의 수치 모의 시나리오와 차이가 마이삭 시기와 비교하여 상대적으로 차이가 조금 더 크게 나타났다. 요약하면 JTWC Best Track과 Holland 모델로 생성한 열대 저기압성 바람장을 이용한 파랑 수치 모의 시나리오(Holland-Komen, Holland-ST6)는 기상 수치모델의 해상풍 자료를 입력 외력으로 사용하였을 때와 비교하여 전체적으로 유의파고 및 첨두주기의 모의 결과에서 더 좋은 결과를 보이지 못했다. 또한 앞서 언급하였듯이 Holland 모델은 Best Track 자료의 품질에 따라 생성되는 해상풍의 정확도가 변할 수 있으며, 한정된 시간 내의 국지적인 범위의 자료를 생성한다. 따라서 취송시간과 거리가 영향을 끼치는 파랑 수치 모의에서, Holland 모델로 생성한 태풍 바람장은 폭풍파 수치 모의의 입력 외력으로서 활용도가 떨어진다고 판단된다.
5. 결 론
본 연구에서는 기상청과 일본기상청의 기상 예보모델인 RDAPS와 JMA-MSM의 해상풍 자료를 입력 외력으로 사용하여 2020년 태풍 마이삭과 하이선에 의해 발생한 폭풍파를 수치모의 하였다. 또한 기상 예보모델의 태풍 시기 바람 예측 정확도와 그에 따른 파랑 수치모의 결과를 비교 및 검증하기 위해 JTWC의 Best Track 자료와 Holland et al.(2010) 기법으로 태풍 시기의 해상풍 자료를 재현하여 파랑 수치 모델의 입력 외력으로 사용하였다. 파랑 수치모의에서 지배방정식의 원천항은 보편적으로 사용되는 Komen et al.(1984)의 식과 현장 관측연구 기반으로 개발된 원천항인 ST6 (Rogers et al.,2012)를 사용하였다. 각 입력 외력과 사용 원천항 별로 파랑 수치모의 시나리오를 구성하여 파랑 수치모의를 실시하여 얻어진 결과를 비교, 분석 및 검증을 실시하였다.
본 연구의 결과를 요약하자면 다음과 같다:
- 입력 외력 검증에서 RDAPS와 JMA-MSM의 해상풍 자료 모두 태풍 시기의 풍속을 과대 추정하였다. 하지만 RDAPS의 풍속이 JMA-MSM에 비해 더 낮은 RMSE 값을 가지며, 외해 정점에서의 태풍 시기의 풍속을 더 정확히 재현하였다.
- JTWC Best Track 자료와 Holland et al.(2010)의 기법을 사용하여 구축한 태풍 해상풍은 마이삭과 하이선 내습 시기마다 재현도의 차이를 보였다(태풍 하이선의 재현도가 마이삭에 비해 상대적으로 떨어짐). 종합적으로 입력 외력 해상풍 자료의 시공간적인 범위나 정확도 측면에서 기존의 기상 수치예보 모델(RDAPS, JMA-MSM)보다 더 나은 점을 찾을 수 없었다.
- 기상 예보모델의 해상풍 자료를 입력 외력으로 사용한 유의파고 수치 모의 결과에서, 입력 외력 풍속의 과대 추정으로 인해 전체적으로 태풍 시기의 유의파고를 과대 추정한 것으로 판단되었다. 그 중 RDAPS-Komen의 수치 모의 시나리오가 가장 낮은 RMSE 값을 나타내어, 태풍 마이삭과 하이선 시기의 유의파고를 가장 잘 모의하였다.
- 기상 예보모델을 해상풍 자료를 입력 외력으로 사용한 첨두주기 수치 모의 결과에서, 외해에서 발생한 첨두주기의 관측오차의 한계로 낮은 R2 값을 나타내었다. 따라서 시나리오별 파랑 수치모의 결과를 비교할 수 없었다.
- Holland 모델로 구축한 해상풍 자료를 사용한 파랑 수치 모의 결과에서, Best Track 자료의 정확성과 Holland 모델로 생성한 바람장이 특정 기간의 국지적인 범위에 한계가 존재한다는 단점이 있어, 파랑 수치모의에 입력 외력으로 적합하지 않았고 판단하였다.
이를 통해 다음과 같은 결론을 얻을 수 있다:
- SWAN은 장주기성 고파랑의 환경에서 유의파고를 과소 추정하는 경향이 있다 (Son and Do, 2021; Do and Kim, 2018). 본 연구를 통해 ST6를 사용하였을 때 장주기성 고파랑의 환경에서 전체적으로 감쇠되는 파랑 에너지를 줄여, Komen의 원천항을 사용하였을 때와 비교하여 유의파고를 더 높게 모의할 수 있다는 결과를 도출하였다.
- 본 연구에서는 입력 외력으로 사용한 RDAPS와 JMA-MSM의 해상풍이 태풍 시기 풍속을 과대 추정하였기 때문에 모든 수치 모의 시나리오에서 유의파고를 과대 추정한 것으로 판단하였다. 그렇기에 가장 유의파고를 낮게 모의한 RDAPS-Komen이 유의파고를 가장 잘 모의한 결과를 나타내었지만, 이를 통해 ST6가 태풍 시기의 폭풍파 수치모의에 적합하지 않다고 판단하기 어렵다.
- 정확한 해상풍 자료를 입력 외력으로 사용할 수 있는 최적의 수치 모의 시나리오를 가정할 때, ST6가 Komen의 원천항보다 장주기성 고파랑의 환경에서 유의파고를 더 정확하게 모의할 수 있을 것으로 판단된다.
- 대한민국 해역에서 태풍으로 인한 폭풍파의 수치 모의 연구에서는 주로 JMA-MSM의 해상풍 자료를 입력 외력으로 사용하였다 (Kim et al., 2020; Kwon et al., 2020; Yoon et al., 2020). 하지만 본 연구에서는 RDAPS와 JMA-MSM의 해상풍 자료의 풍속과 이를 활용한 파랑 수치 모의 결과를 비교하여, 폭풍파의 수치 모의 입력 외력으로서 RDAPS의 적합성을 검증하였다.
- 파랑 수치 모의에서 입력 외력으로 사용되는 해상풍 자료의 정확도가 매우 중요하다는 점을 고려하면, 기상청의 RDAPS의 해상풍 자료는 대한민국 해역의 파랑 수치 모의 입력 외력으로써 유용하게 활용될 수 있다고 판단된다. 하지만 시공간적 변동성이 심한 환경인 극한조건의 기상환경에서 부정확한 결과를 보이는 경향이 있었다. 이는 Kim et al. (2020)에서 시행된 연구와 같이 파랑 수치 모의에서 해상풍 자료에 대한 자료동화 기법을 적용하여, 파랑의 예측 정확도를 향상시킬 수 있을 것으로 기대된다.
- 본 연구에서 시행한 폭풍파 수치 모의는 2개의 태풍 이벤트를 대상으로 하였다. 따라서 다양한 기상 및 파랑 조건에서의 장기적인 파랑 수치 모의를 통해, 대한민국 주변 해역의 파랑 예측에서 RDAPS와 ST6의 적용성을 검토해볼 필요가 있다. 이를 통해 ST6가 Komen의 원천항을 대체할 수 있을 것으로 판단된다.
- 본 연구에서는 폭풍파 수치 모의 검증이 외해의 부이관측자료를 통해 이루어졌다. 그렇기에 외해에서 발생하는 첨두주기 관측오차로 인해, 파랑의 첨두주기 모의 성능을 정확하게 평가할 수 없었다. 따라서 연안으로 전파되어 해저마찰과 수심에 의해 변형되는 폭풍파와, 이에 따른 파랑의 주기성분의 모의 성능을 평가할 수 있는 추가적인 연구가 필요하다. 이는 추후 연구에서 비구조격자체계 또는 네스팅 기법을 SWAN에 적용시켜 연안에 적용할 수 있는 모델 구축하여 평가될 수 있을 것으로 기대된다.
Acknowledgements
이 논문은 한국연구재단 이공분야기초연구사업(NRF-2019 R1C1C1003160)과 2021년 해양수산부 재원으로 해양수산과학기술원의 지원(종합해양과학기지 구축 및 활용연구)를 받아 수행된 연구입니다.