표류물의 충돌해석을 위한 LS-DYNA의 적용성 검토

On Applicability of LS-DYNA for Collision Analysis of Drifting Objects

Article information

J Coast Disaster Prev. 2022;9(2):133-143

Publication date (electronic) : 2022 April 30

doi : https://doi.org/10.20481/kscdp.2022.9.2.133

Taegeon Hwang ^*, Taeyoon Kim ^**, Seonyong Choi ^***, Chanhyun Ko ^*, Woo-Dong Lee^,^*

^*Department of Ocean Civil Engineering, Gyeongsang National University, Tongyeong, Korea

^**Institute of Marine Industry, Gyeongsang National University, Tongyeong, Korea

^***Harbor Department, Kunhwa Engineering & Consulting Co., Ltd, Seoul, Korea

황태건^*, 김태윤^**, 최선용^***, 고찬현^*, 이우동^,^*

^*경상국립대학교 해양토목공학과

^**경상국립대학교 해양산업연구소

^***(주)건화 항만부

Corresponding author: Woo-Dong Lee, +82-55-772-9126, wdlee@gnu.ac.kr

Received 2022 March 21; Accepted 2022 April 7.

Trans Abstract

The characteristics of a secondary disaster are not well known with respect to the drift-impact by storm surge or tsunami. A numerical analysis for understanding the characteristics of a secondary disaster must be capable of simulating fluid dynamics as well as structural behaviors. In this sense, a fluid-structure interaction analysis is necessary with specialized numerical model such as LS-DYNA. In this study, we numerically simulated the breakaway-drift-impact process of a container due to break waves using LS-DYNA, and additionally examined the applicability of the model. Furthermore, we investigated the validity and effectiveness of an LS-DYNA analysis through the wave pressure comparison of measured values in a hydraulic experiment and the calculated values. In the analysis of drift-impact of a container due to dam-break waves, the drift velocity had a dominant effect, which is in line with previous experiments. In the collision analysis of drifting object due to storm surge/tsunami, the LS-DYNA simulation was proven as an appropriate numerical approach in this study.

Keywords: Drifting object; Collision force; Wave pressure; Dam-break wave; LS-DYNA

1. 서 론

한반도 주변 해역에서는 지구온난화의 영향으로 규모가 큰 태풍의 내습 빈도가 증가하고, 해저지진의 발생 또한 증가하는 추세이다. 이러한 태풍과 해저지진은 폭풍해일과 지진해일을 동반하며, 연안지역에서 막대한 인적⋅물적 피해를 입힌다. 1차적으로 해일에 의한 월파, 침수, 충격파가 피해 발생시키는 것은 주지의 사실이다. 또한 연안지역에 산재한 선박, 차량, 컨테이너 등의 물체가 표류하여 구조물에 충돌하는 2차 피해의 위험성 역시 간과할 수 없다.

우리나라에서는 2003년 태풍 매미에 의한 선박의 표류, 2006년 태풍 에위니아에 의한 컨테이너의 표류, 2012년 태풍 볼라벤에 의한 선박의 표류에 의한 2차 피해가 다수 보고되었다. 2004년 인도양 수마트라 지진해일과 2011년 동일본 지진해일에 역시 선박, 차량, 컨테이너, 오일탱크 등이 유출-표류-충돌하여 여러 구조물에 피해를 주었다. 이 같은 해일의 2차 재해를 저감시키기 위해서는 물체의 유출-표류-충돌 과정을 이해하여야 한다. 이를 위해서는 대규모 수리모형실험 또는 검증된 수치모델을 이용한 수치해석이 반드시 수반되어야 한다. 여기서 고정도의 수치해석은 수리모형실험을 대체할 수 있고, 해일의 유체운동과 구조물의 거동을 함께 검토할 수 있는 유체-구조 상호작용 해석이 필요하다.

국외에서는 해일에 의한 표류물의 2차 재해에 관한 실험적 및 수치적 연구가 다수 수행되었다. Kentaro et al.(2006)은 지진해일에 의해 컨테이너의 표류 속도와 충돌 방향이 충돌력에 지배적 영향을 미친다는 것을 유체와 구조의 커플링 해석을 통해 밝혀내었다. Yeom et al.(2009)의 수리모형 실험에서는 표류 컨테이너의 충돌력을 측정하였다. 그리고 수치파동수조에서는 표류해석, LS-DYNA에서는 충돌해석을 각각 수행하였다. Madurapperuma and Wijeyewickrema(2012)는 LS-DYNA에서 임의의 표류속도를 가진 컨테이너와 기둥과의 충돌해석으로부터 기둥의 파괴, 축력 변화, 바닥 변위에 대해 분석하였다. Riggs et al.(2013)은 나무 전신주와 20ft 컨테이너를 이용한 실제 규모의 충돌실험을 수행하였다. 그 결과, 진자운동에 의한 컨테이너의 종방향 충돌에서 최대 하중을 나타내었다. 그리고 물에 의한 표류-충돌에서는 예상치 못한 하중이 부과됨을 확인하였다. Ko et al.(2015)은 진자 운동에 의한 충돌, 물에 의한 표류-충돌을 비교하였으며, 표류-충돌에 의한 하중이 최대 17%, 충돌 시간이 평균적으로 20% 증가한다고 보고하였다. Yeom et al.(2017)은 지진해일 내습조건의 수리모형실험에서 측정한 컨테이너의 충돌력과 LS-DYNA의 충돌해석결과를 토대로 기존 충돌력 산정식(Mizutani et al., 2005)을 개량하였다.

국내에서는 2003년 태풍 매미 내습 이후, 폭풍해일 예측, 침수해석 등에 관한 연구가 활발히 수행되고 있다. 그리고 수리모형실험과 수치해석을 통해 지진해일 또는 고립파의 수리특성(Lee et al., 2019; Mase et al., 2020)을 논의할 뿐, 해일에 의한 표류물의 거동 및 충돌 재해에 대한 검토가 거의 이루어지지 않았다. Yeom et al.(2009)이 해일에 의한 표류 컨테이너의 충돌력을 LS-DYNA를 이용하여 산정하였다. 이때, 계산부하가 큰 비선형 동적 구조해석모델 LS-DYNA로 표류 거동까지 재현하지 못하였고, 슈퍼컴퓨터를 이용해 충돌 현상만 모의하였다. Choi(2020)는 해일표류물과 철근콘크리트와의 충돌실험에서 표류물을 진자운동으로 고려하여 충돌력을 측정하였다.

최근에는 비약적으로 컴퓨터의 계산성능이 향상됨에 따라 LS-DYNA를 PC에서 구동할 수 있는 환경이 조성되었다. 이에 Hwang et al.(2021)은 LS-DYNA를 이용해 초대형 컨테이너선의 스러스터 흐름이 안벽의 안정성에 미치는 영향을 검토하였다. Seo et al.(2022)는 산사태 지진해일의 전파과정을 LS-DYNA를 이용하여 조사하였다. 그 밖에 해안 및 해양공학 분야에서도 LS-DYNA 해석(Lee et al., 2019; Kim et al., 2021)이 증가하고 있다.

본 연구에서는 해일에 의한 물체의 유출-표류 거동뿐 아니라, 표류물의 충돌해석까지 LS-DYNA에서 적용할 수 있는지에 대한 검토를 수행한다. 먼저 LS-DYNA의 타당성 및 유효성을 검증하기 위해 Kleefsman et al.(2005)의 실험결과와 비교한다. 그리고 붕괴파에 의한 컨테이너의 표류 및 충돌 특성을 분석하고, 붕괴파 규모에 따른 충돌력을 산정한다.

2. LS-DYNA

LS-DYNA는 유한요소 해석프로그램으로 양해법(Explicit)에 기초하여 충돌, 파괴, 재료 성형 등 복잡한 비선형 문제를 푸는 것에 특화되었다. 그러므로 유체-구조 상호작용(FSI; Fluid-Structure Interaction)에 따른 복잡한 유체운동 및 구조물의 거동을 직접 해석할 수 있다.

2.1 지배방정식

ALE(Arbitrary Lagrangian Eulerian)기법(Santini et al., 1998; Souli et al., 2000; Seddon et al., 2004; Poehlmann-Martins et al., 2005)은 Lagrangian 구조물과 Eulerian 유체영역의 커플링을 통해 구조-유체 비선형 상호작용을 직접 해석하며, 과도한 변형에 따른 요소의 수정, 수정된 요소의 물성치를 재계산한다. ALE 방정식의 물성 시간 미분과 공간 시간 미분 사이의 관계는 다음과 같다.

(1) ∂f(Xi,t)∂t=∂f(xi,t)∂t=(vi-ui)∂f(xi,t)∂xi=∂f(xi,t)∂t-wi∂f(xi,t)∂t

여기서 X_i는 Lagrangian 좌표계, x_i는 Eulerian 좌표계, i는 참고 좌표계, v_i와 u_i는 재료(Lagrangian)와 매쉬(Eulerian)의 유속이다.

LS-DYNA에서 ALE기법은 유한요소법에서 보존 방정식을 사용하여 요소간 질량, 에너지, 운동량 이동을 추적한다. ALE 기법의 질량, 운동량, 에너지 보존에 관한 방정식은 다음과 같다.

(2) ∂ρ∂t=(-ρ)÷(v)-(vi-ui)∂ρ∂xi

(3) ρ∂vi∂t=σi,j-ρ(vi-ui)∂vi∂xj

(4) ρ∂e∂t=σijɛij-ρ(vi-ui)∂e∂xj

여기서 ρ는 재료의 밀도, v_i는 재료의 속도, σ_ij는 스트레스 텐서, ϵ는 스트레인 텐서, e는 내부에너지, u_i는 매쉬의 속도, t는 시간이다.

2.2 LS-DYNA의 검증

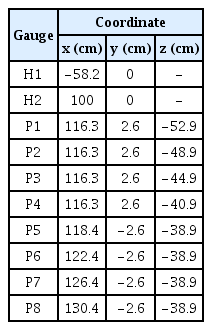
해일에 의한 표류물의 충돌해석에 있어서 LS-DYNA의 적용성을 확인하기 위해 Kleefsman et al.(2005)의 붕괴파 실험과 비교⋅검토한다. Fig. 1은 LS-DYNA의 타당성 및 유효성을 검증할 목적으로 구성한 Kleefsman et al.(2005)에 기초한 길이 322cm, 높이 100cm, 폭 100cm의 수치수조를 구성된다. 붕괴파 생성을 위한 정지상태의 수괴는 길이 122.8cm, 높이 55cm, 폭 100cm이다. 수괴로부터 116.3cm 떨어진 지점에 길이 40.3cm, 폭 16.1cm, 높이 16.1cm의 불투과성 육면체를 바닥에 고정한다.

Fig. 1

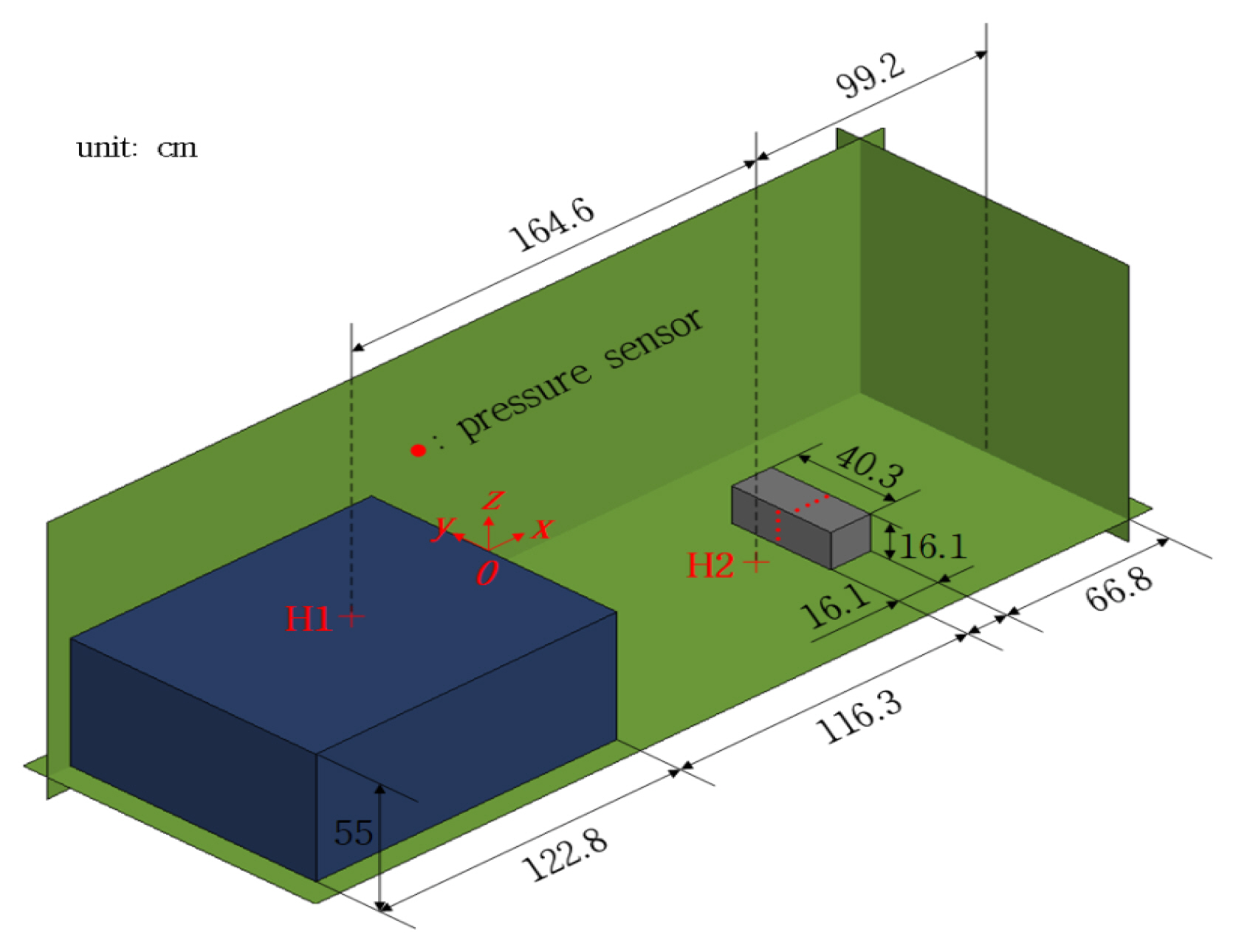
Definition sketch of a numerical water tank including an impermeable box based on the experiment by Kleefsman et al.(2005)

붕괴파의 전파과정에서의 수위변화를 측정하기 위한 파고계 2개, 충격파압 측정하기 위한 구조물의 전면에 4개, 상부에 4개가 각각 설치된다. 파고계 및 파압계의 설치지점은 Table 1과 같다.

Table 1

The wave and pressure gauge locations

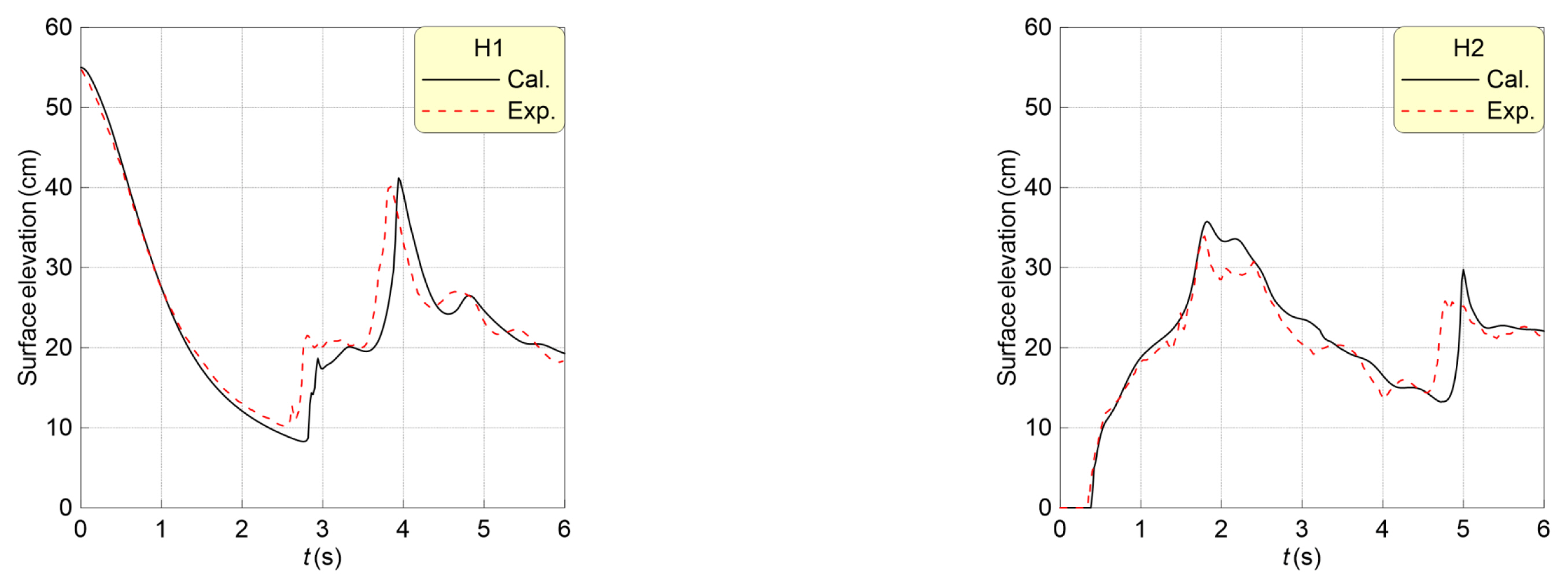
붕괴파의 전파과정을 검증하기 위해 실험사진과 LS-DYNA 시뮬레이션을 Fig. 2에서 비교한다. LS-DYNA에서 계산된 붕괴파의 전파속도가 Kleefsman et al.(2005)의 실험보다 조금 느린 것을 확인할 수 있다. 그 영향으로 인해 H1과 H2에서 계측된 Fig. 3의 수위분포에서도 위상차가 발생한다. H1의 수위분포를 살펴보면, 수괴 붕괴에 따른 수위하강, 구조물에 의한 반사파, 수조 경계에서의 반사파가 순차적으로 나타난다. 그리고 H2에서는 충격파에 의한 구조물 전면의 수위상승 현상이 발생한다.

Fig. 2

Snapshots of dam-break simulation using LS-DYNA compared with the experiment at t=0.4s and 0.56s.

Fig. 3

Comparison between the measured and the calculated surface elevations at H1 and H2

구조물에 작용하는 충격파압을 Fig. 4에서 비교한다. 여기서 P1-P4와 P5-P8은 구조물 전면과 상부에 부착된 파압계로부터 얻어진 압력분포를 각각 나타낸다. LS-DYNA에서 계산된 붕괴파 전파속도가 조금 늦어짐에 따라 구조물 전면에 작용하는 충격파압의 피크 위상 역시 지연된다. 구조물 전면 하단 P1에서 가장 큰 충격파압이 작용하고, 위로 갈수록 피크값이 감소하는 경향을 보인다. 그리고 수조 경계의 반사파에 의한 2번째 피크 위상도 LS-DYNA 결과가 실험보다 조금 느리다. 그리고 구조물 상부의 P5-P8에서 계산된 파압은 전체적으로 전면 파압보다 작고, 실험과 유사한 분포를 나타낸다.

Fig. 4

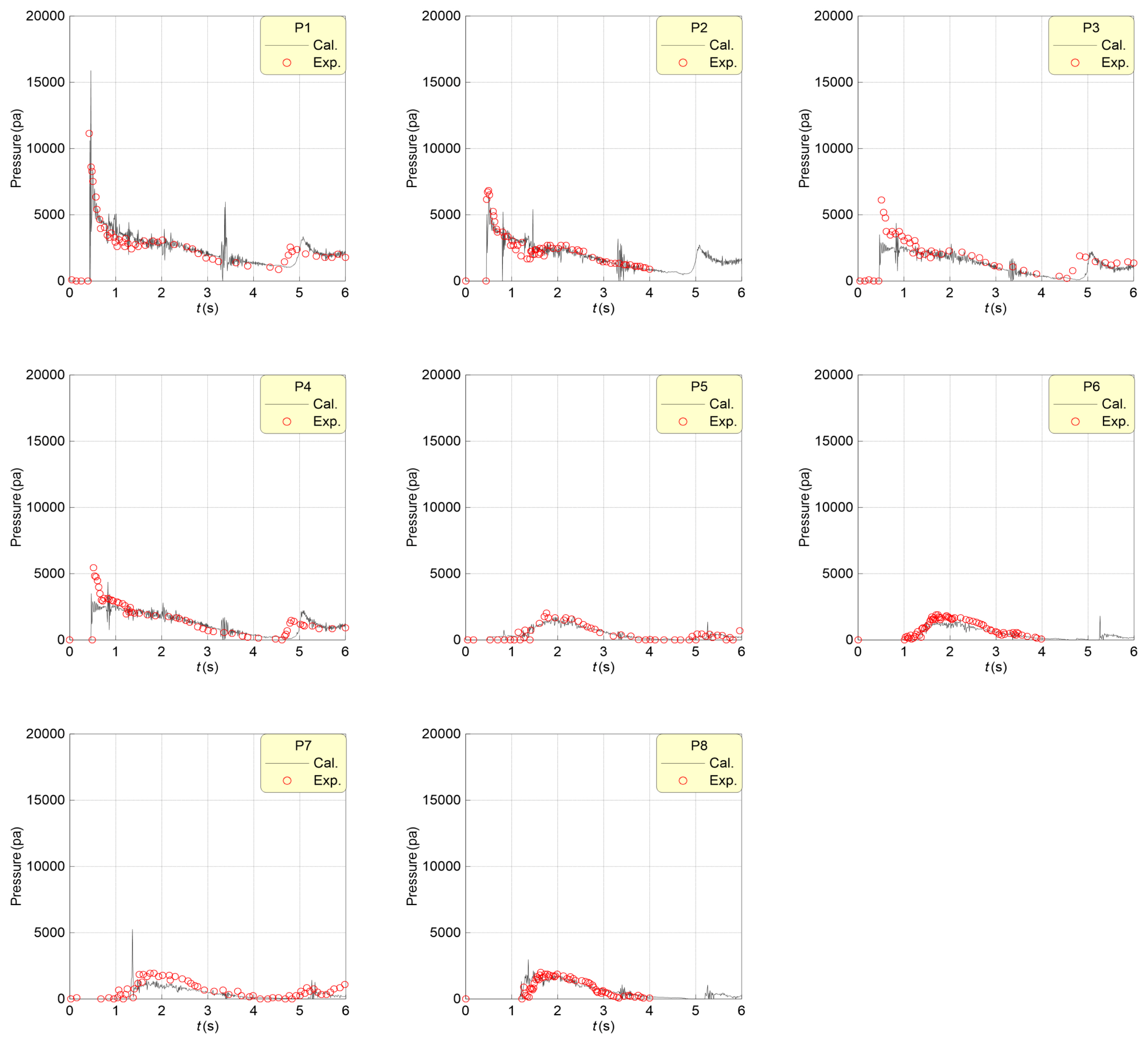
Comparison between the measured and the calculated wave pressures at P1, P2, P3, P4, P5, P6, P7 and P8

붕괴파의 전파속도가 Kleefsman et al.(2005)의 실험과 조금 차이를 보이나, 붕괴파에 의한 충격파압 특성을 전반적으로 잘 재현하고 있다. 이로써 본 연구에서 충돌해석의 적용성을 검토하는 LS-DYNA의 유효성 및 타당성이 어느 정도 검증된 것으로 판단된다.

2.3 계산조건

해일에 의한 표류물의 출동해석에 있어서 LS-DYNA의 적용성을 검토하기 위해 Fig. 5와 같은 길이 24m, 폭 20m의 수치수조를 구성한다. 경계에서의 반사파 발생을 억제하기 위해 수치수조 끝에는 개경계조건을 설정한다. 수괴와 컨테이너, 컨테이너와 기둥과의 거리는 5m, 10m로 모든 계산에서 동일하다. 충돌해석에는 20피트 컨테이너는 ISO 규격의 6.096m, 폭 2.438m, 높이 2.62m, 만재 중량 24,000kg을 적용한다. 컨테이너 부두에서 많이 사용되는 J100 크레인의 다리의 제원을 참고하여 1.732m×1.34m×10m의 직사각형 기둥으로 구성한다.

Fig. 5

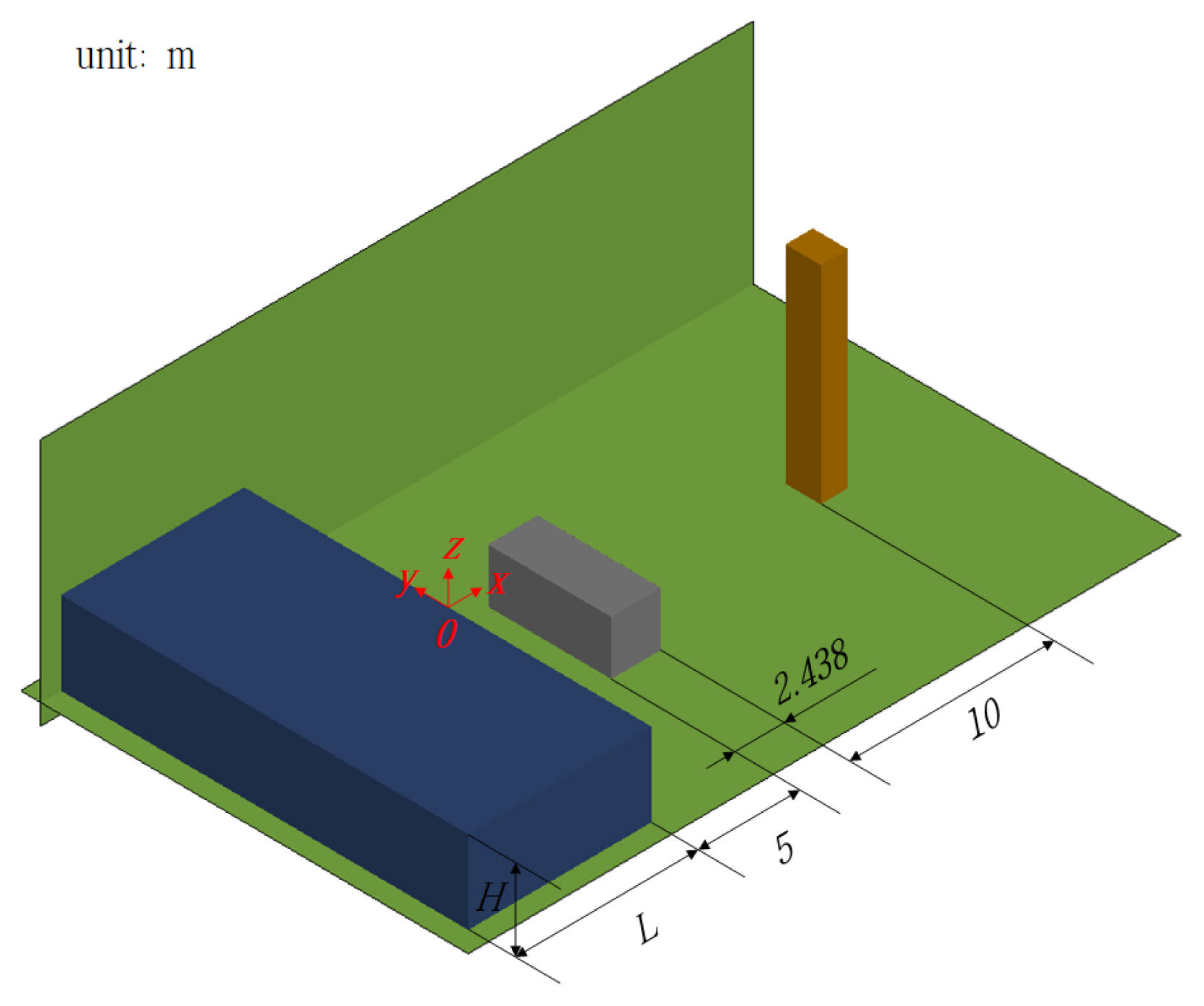
Definition sketch of a numerical water tank including a fixed column and a movable container used in this study

해일의 전파과정까지 모의할 수 없는 관계로 붕괴파를 고려하여 LS-DYNA에서는 컨테이너의 유출-표류-충돌 과정을 모의한다. 정지상태의 초기 수괴의 제원을 달리하여 붕괴파 규모를 조절한다. 초기 수괴의 높이(H)와 길이(L)는 1-9m를 각각 적용한다. 17가지 붕괴파 조건과 컨테이너 유무를 각각 고려하면, 총 34가지의 수치계산을 수행한다.

3. 충돌해석 결과

3.1 붕괴파의 전파과정

Fig. 6과 Fig. 7은 수치수조에서 붕괴파의 전파과정을 나타낸 것이며, Fig. 6은 컨테이너가 없이 붕괴파만 발생하는 조건, Fig. 7은 붕괴파에 의해 컨테이너가 유출-표류-충돌하는 경우이다.

Fig. 6

Dam-break wave propagation on H=9m and L=9m conditions in a numerical water tank with a fixed column

Fig. 7

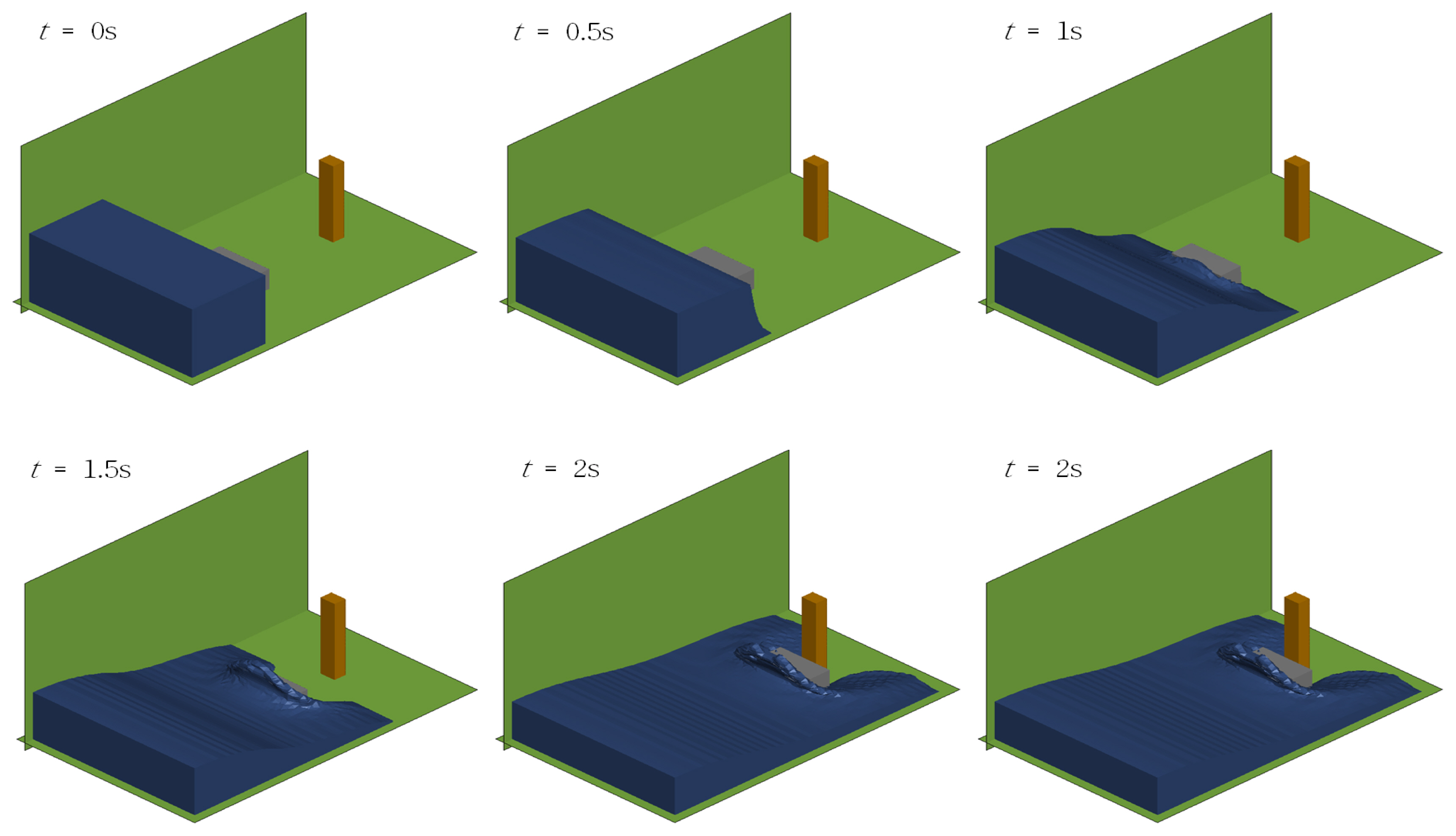
Dam-break wave propagation on H=9m and L=9m conditions in a numerical water tank with a fixed column and a movable container

정지해 있던 수괴가 붕괴되어 생성된 파가 사각 기둥을 덮치는 것을 Fig. 6에서 확인할 수 있다. 기둥 전면에서는 처오름이 발생하고, 양쪽 측면에서는 대칭적 처오름 그리고 배후에는 차폐영역이 발생한다. Fig. 7에서 붕괴파에 의해 컨테이너의 유출-표류-충돌 과정을 확인할 수 있다. 또한 표류 컨테이너가 기둥과 충돌한 후에도 붕괴파가 지속 작용한다.

3.2 파력 및 충돌력 분포

3.2.1 붕괴파의 파력

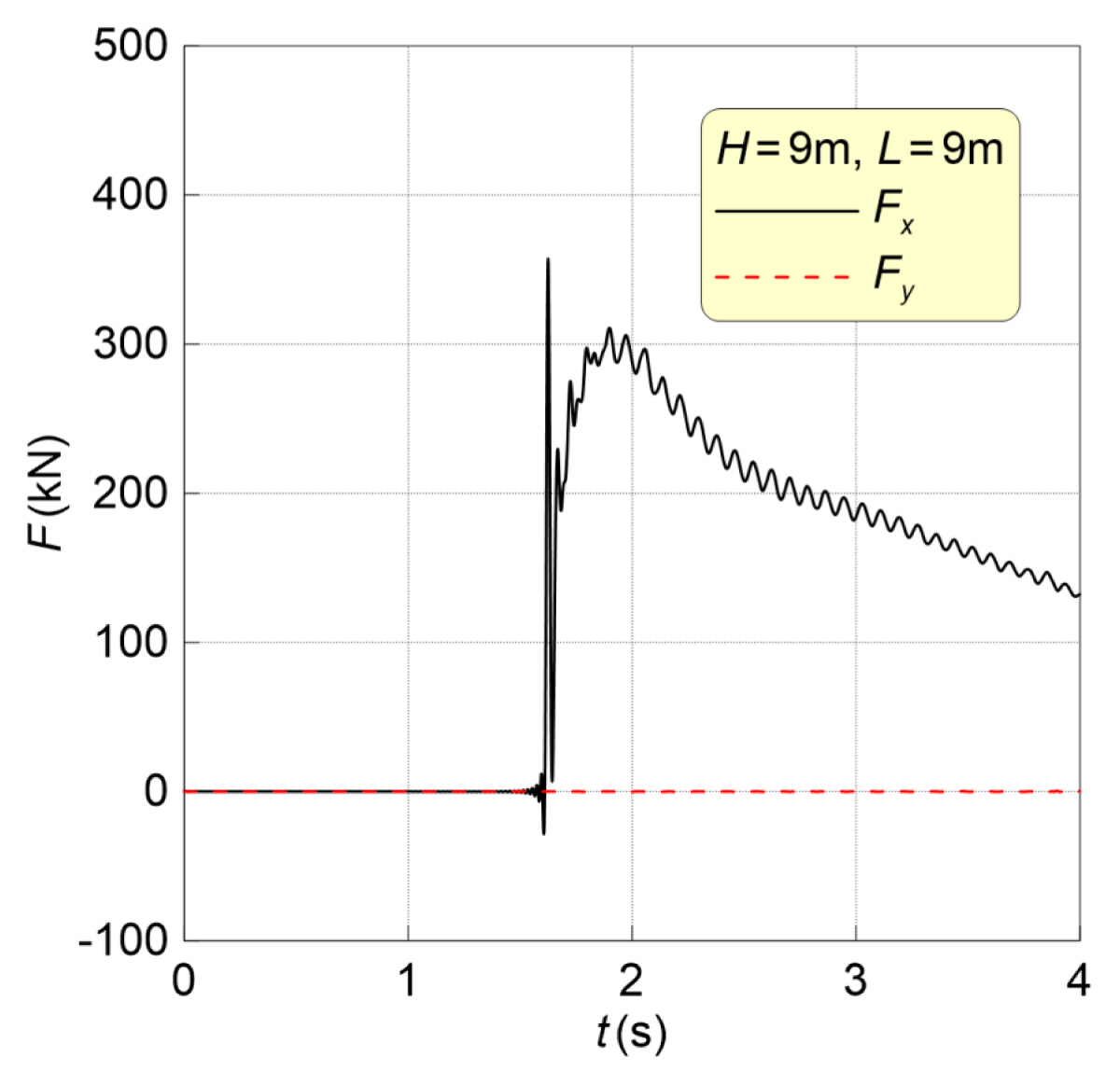
H=9m, L=9m 조건의 붕괴파가 기둥에 작용할 때, 나타나는 x, y방향 수평력(F_x, F_y)의 시간분포를 Fig. 8에 각각 나타낸다. 여기서 검정 실선은 F_x(붕괴파 진행방향이 양의 값), 붉은 점선은 F_y를 각각 의미한다.

Fig. 8

Dynamic horizontal forces acting on a column due to the impact of dam-break wave

기둥의 양쪽 측면에 붕괴파의 처오름 현상이 대칭적으로 발생하기 때문에 F_y가 상쇄되는 것을 Fig. 6에서 확인할 수 있다. 기둥 배후에는 파동의 영향이 전달되지 않기 때문에 붕괴파 진행방향의 힘(+F_x)이 지배적이고, 충격파가 발생하는 시점에 최대값이 발생한다. 그리고 유수에 의해 바닥이 고정된 기둥에 작용하는 유체력이 진동하는 것으로 것을 알 수 있다.

붕괴파에 의해 지배적으로 작용하는 F_x분포를 붕괴파 규모에 따라 Fig. 9와 Fig. 10에 각각 나타낸다. Fig. 9는 정지수괴의 길이(L)가 9m일 때, 높이(H) 변화에 따른 유체력 분포이다. Fig. 10은 H=9m일 때, L에 따른 유체력 분포이다. 여기서 명암이 짙은 선일수록 H 또는 L이 큰 조건을 나타낸다.

Fig. 9

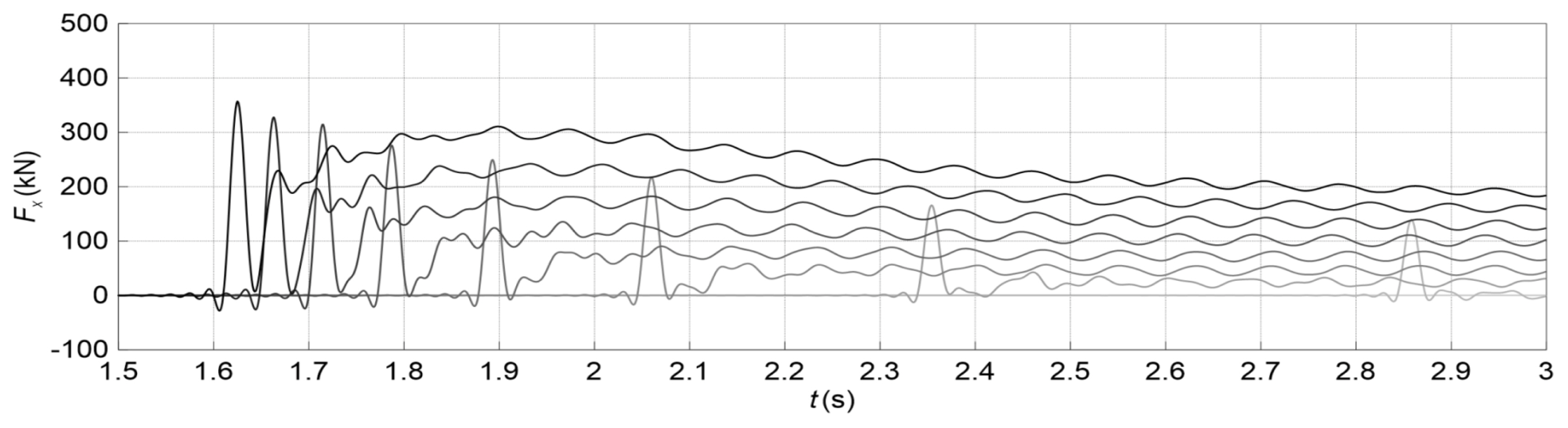
Time-domain fluid force acting on a column in the propagation direction of dam-break wave due to the variation of H

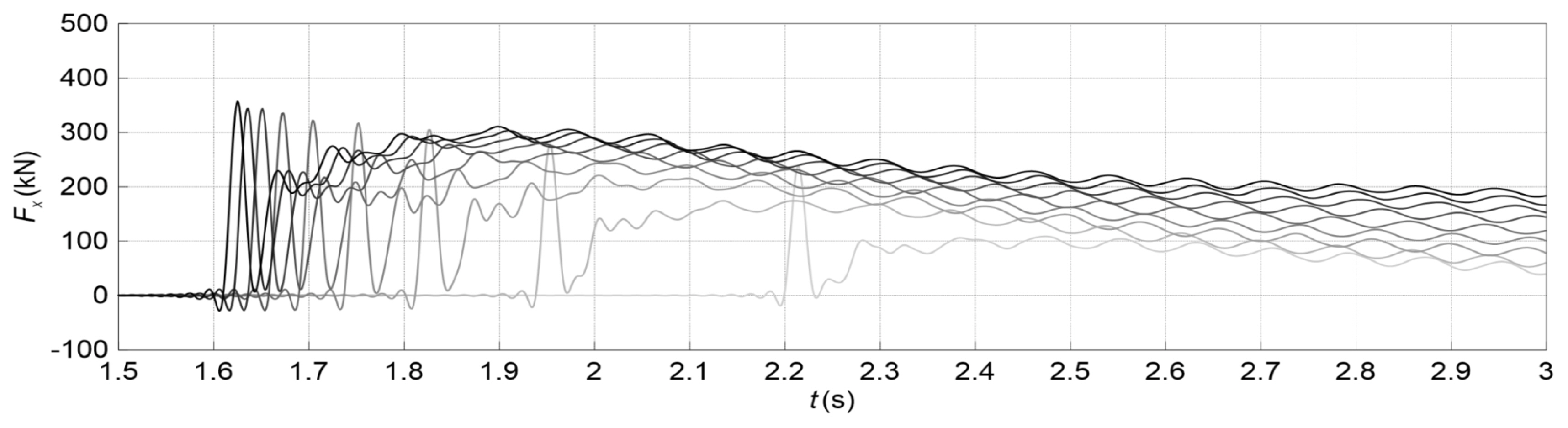
Fig. 10

Time-domain fluid force acting on a column in the propagation direction of dam-break wave due to the variation of L

정지수괴와 기둥 사이의 거리가 같은 경우, L이 일정하고, H가 클수록 파속이 빠르기 때문에 붕괴파가 먼저 도달하는 것을 Fig. 9에서 확인할 수 있다. 그리고 H가 클수록 기둥에 작용하는 F_x가 전체적으로 크다. Fig. 10로부터 일정한 H조건에서 L이 클 경우, 붕괴파의 수위하강이 느리다. 그 때문에 전파속도 차이는 크지 않으며, L≤5m에서는 피크값의 시간차가 0.1s 이하이다. 정지수괴의 L이 클수록 기둥에 작용하는 F_x가 증가하나, 그 차이는 크지 않다.

3.2.2 표류물의 충돌력

Fig. 11은 H=9m, L=9m 조건의 붕괴파에 의한 표류 컨테이너가 기둥과의 충돌과정에서 나타내는 x와 y방향 수평력(F_x, F_y)의 시간분포이다. 여기서 검정 실선은 F_x, 붉은 점선은 F_y를 각각 나타낸다.

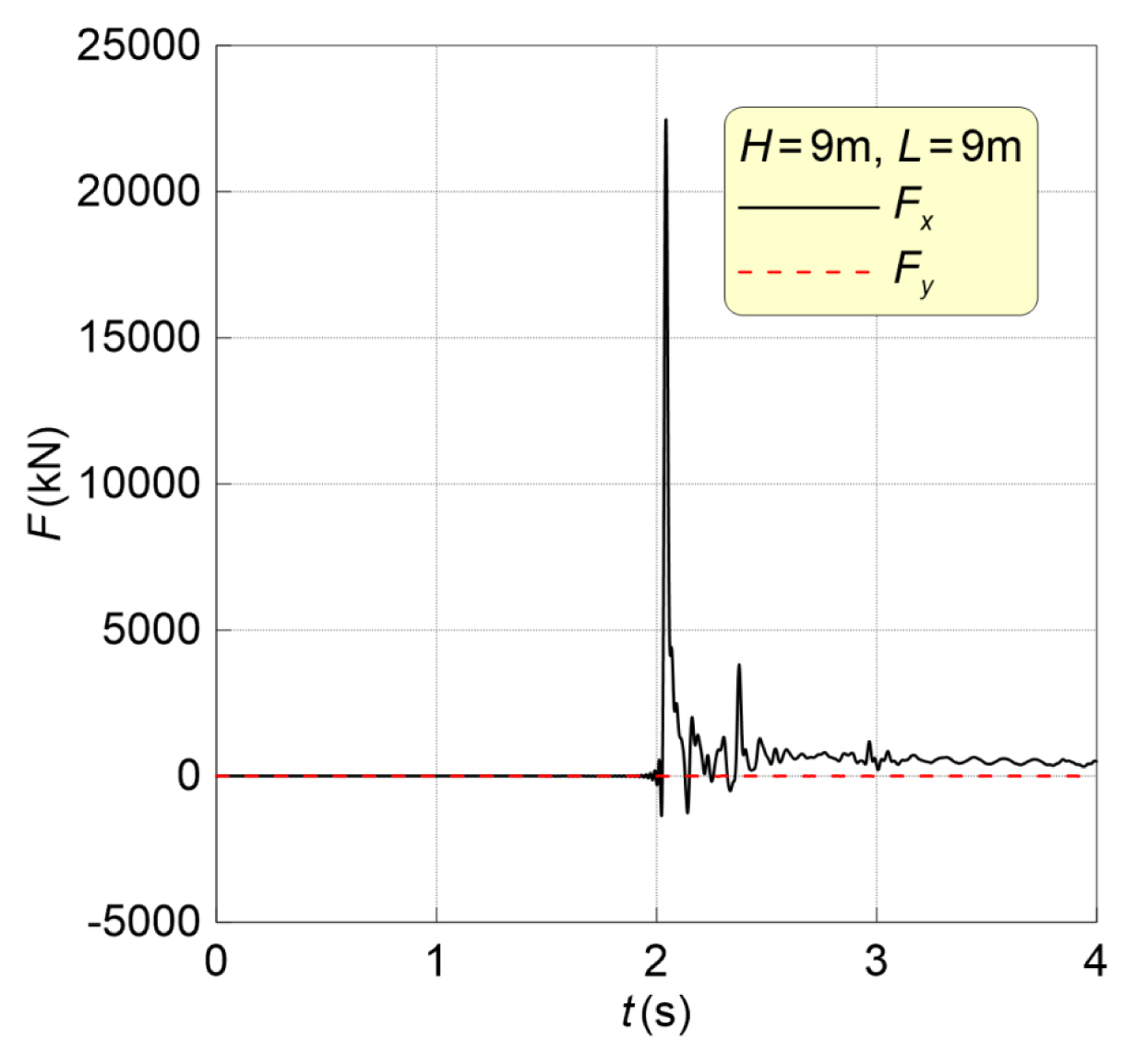
Fig. 11

Dynamic horizontal forces acting on a column due to the impact of dam-break wave with a drift container

Fig. 11로부터 붕괴파에 의해 유출된 표류 컨테이너가 기둥과 충돌함에 따라 표류 방향의 힘(+F_x)이 크게 발생한다. 컨테이너가 없는 Fig. 8처럼 기둥의 양쪽 측면에서 붕괴파가 대칭적으로 유입됨에 따라 F_y는 미소하게 나타난다. 컨테이너의 1차 충돌에서 최대 충돌력이 발생하고, 이후에도 붕괴파가 지속 작용함에 따라 재차 기둥과 충돌하는 것을 알 수 있다.

표류 컨테이너의 지배적 충돌력이 나타나는 F_x의 시간분포를 붕괴파 규모에 따라 Fig. 12와 Fig. 13에 각각 나타낸다. Fig. 12와 Fig. 13은 정지수괴가 L=9m과 H=9m일 때, H와 L에 따른 유체력 분포를 각각 나타낸 것이다. 여기서 명암이 짙은 선일수록 H 또는 L이 큰 조건이다.

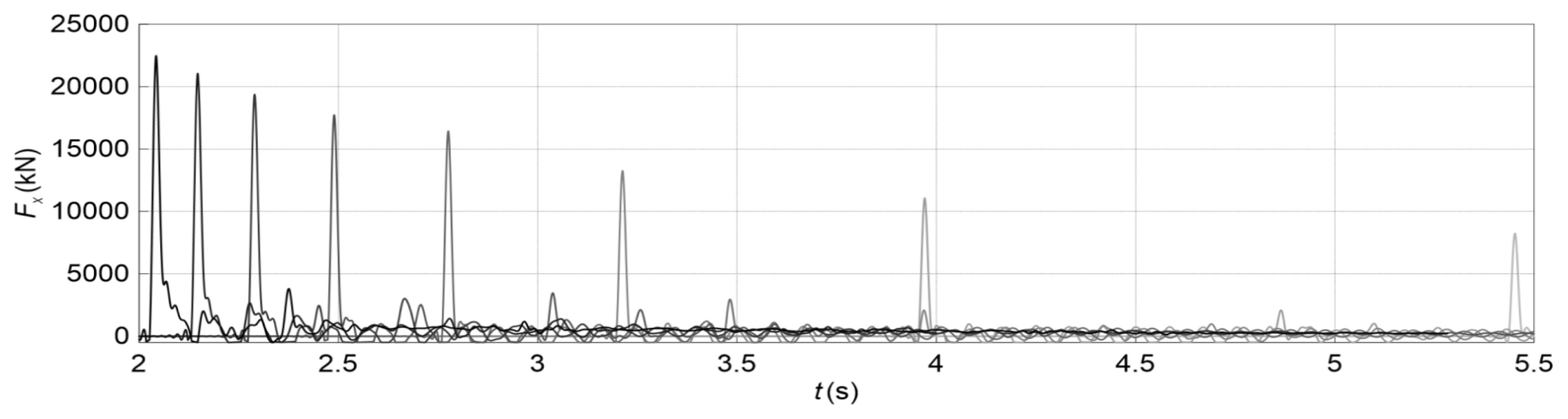
Fig. 12

Time-domain collision force acting on a column in the propagation direction of dam-break wave due to the variation of H

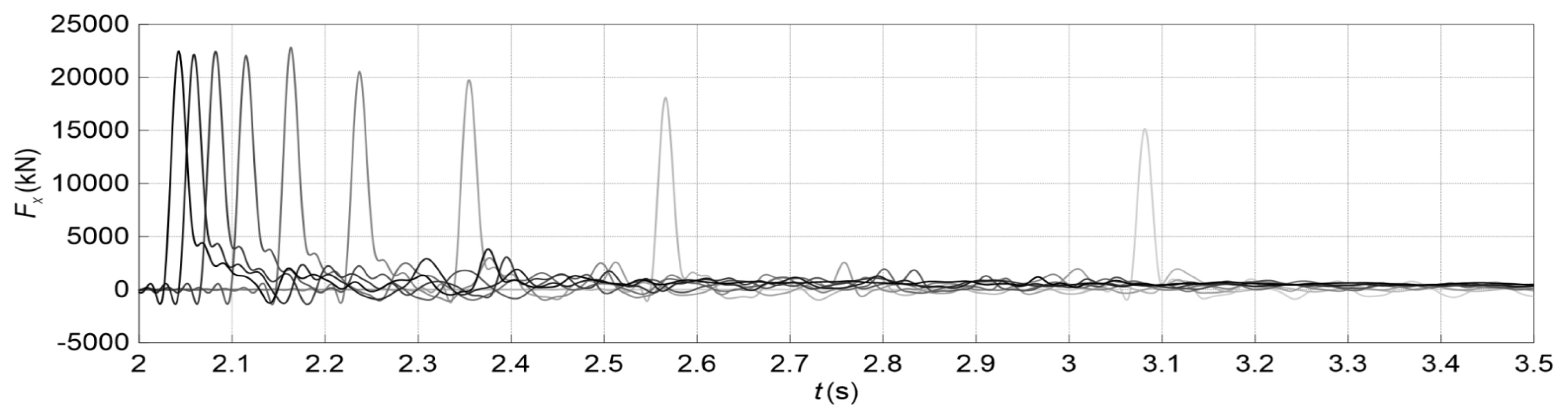
Fig. 13

Time-domain collision force acting on a column in the propagation direction of dam-break wave due to the variation of L

정지수괴와 컨테이너, 컨테이너와 기둥과의 각 거리가 일정한 조건에서 L이 같고(L=9m), H가 클수록 붕괴파의 전파 속도가 빠르다. 그 영향으로 Fig. 12처럼 붕괴파에 의한 표류 컨테이너도 H가 클수록 충돌시간이 빠르다. 그리고 H가 클수록 컨테이너의 충돌속도 역시 빠름으로 기둥에 작용하는 F_x가 전체적으로 크다. Fig. 10에서 확인한 것처럼 H=9m 조건에서 L≧5m의 피크값 시간차는 0.1s 이하이지만, L이 클수록 컨테이너의 표류속도 역시 빨라진다. 전반적으로 L이 클수록 붕괴파에 의한 표류 컨테이너의 충돌에 따른 F_x가 커지는 경향을 보인다. 다만, L≧5m 조건에서 F_x의 차이는 크지 않고, 컨테이너와 기둥이 면대면으로 충돌하는 L=5m에서 가장 큰 피크값을 나타낸다.

3.3 충격파력 및 최대 충돌력

3.3.1 붕괴파의 충격파력

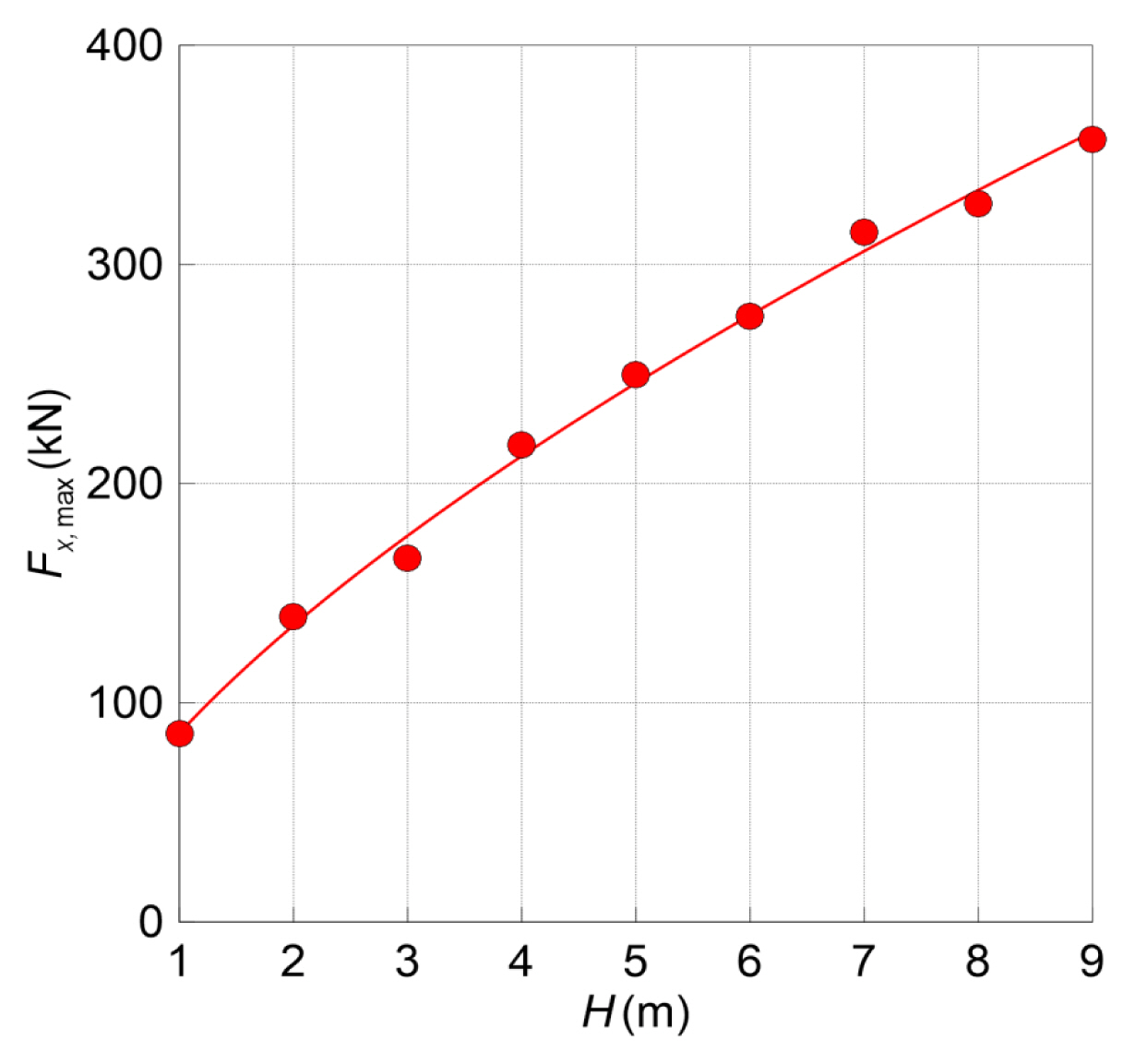
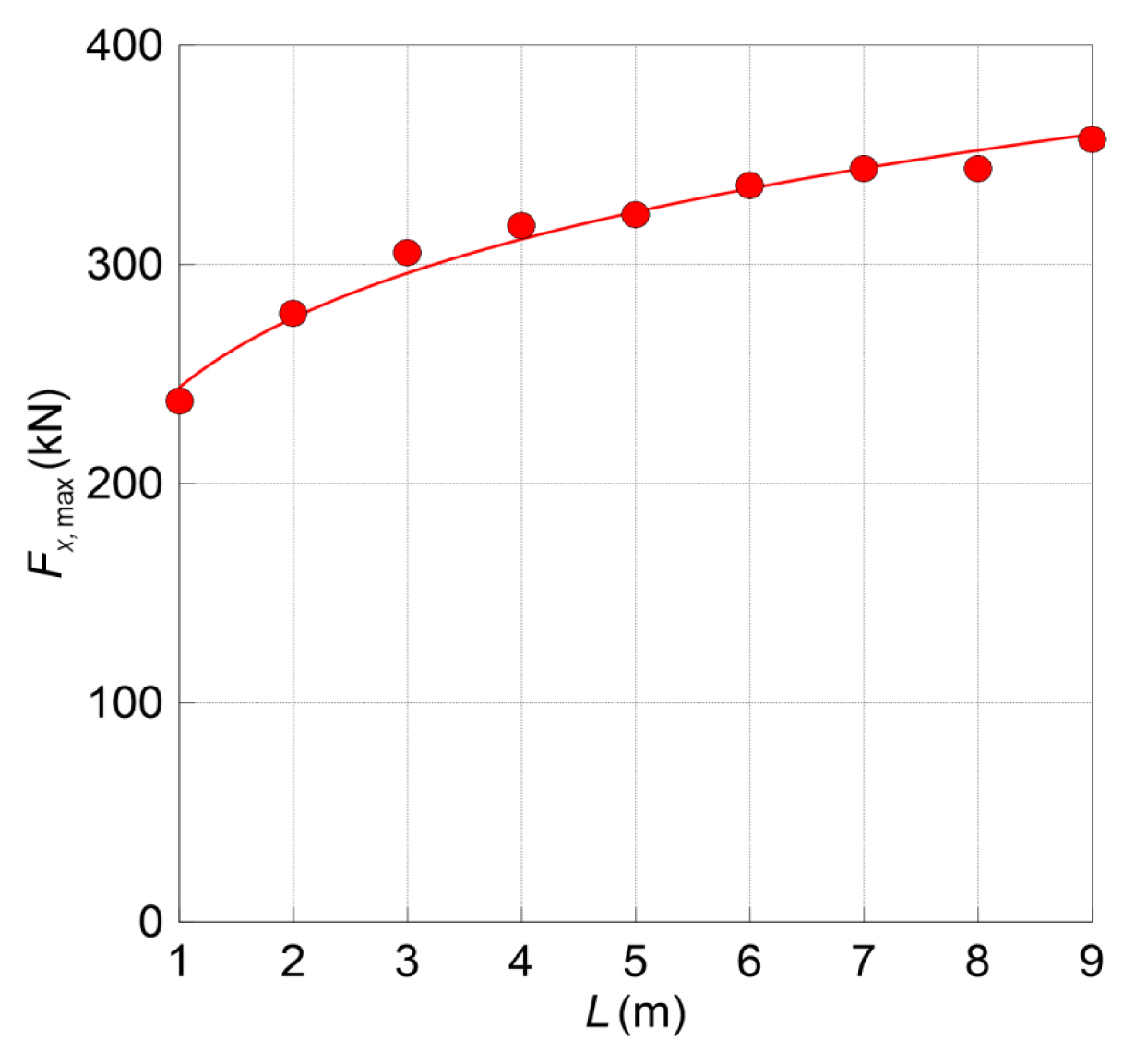
컨테이너가 없는 조건에서 붕괴파 모의에서 계산된 기둥에 작용하는 최대 수평력(F_x,max)을 Fig. 14와 Fig. 15의 그래프에 도시한다. Fig. 14와 Fig. 15는 각각의 L=9m, H=9m의 고정조건에서 H와 L에 따른 값을 나타낸 것이다.

Fig. 14

Impulsive wave force acting on a column due to the variation of H

Fig. 15

Impulsive wave forces acting on a column due to the variation of L

Fig. 14에서 정지수괴의 L이 9m일 때, H가 증가할수록 붕괴파의 전파속도, 처오름이 증가하는 관계로 기둥에 작용하는 F_x,max 역시 증가한다. Fig. 15로부터 H=9m 조건에서 L에 따른 붕괴파의 전파속도 및 처오름이 증가하여 F_x,max가 증가하는 경향을 나타내지만, F_x,max의 차이는 크지 않다. 그리고 앞서 확인한 것과 같이 L≧5m 조건에서는 0.1초 이내의 차이를 두고, 붕괴파가 기둥에 충돌함으로 F_x,max의 차이가 작음을 알 수 있다.

3.3.2 표류물의 최대 충돌력과 충돌속도

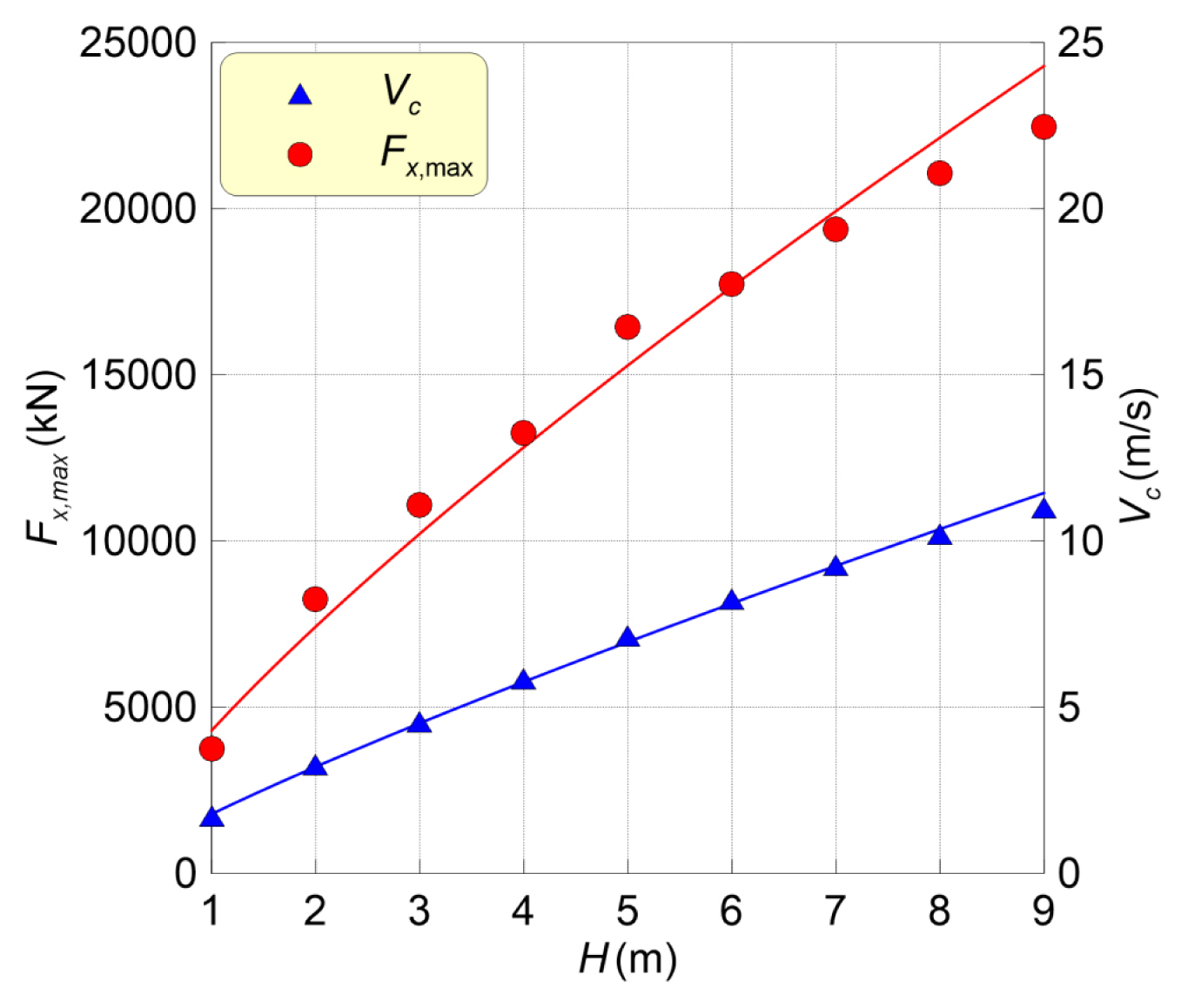
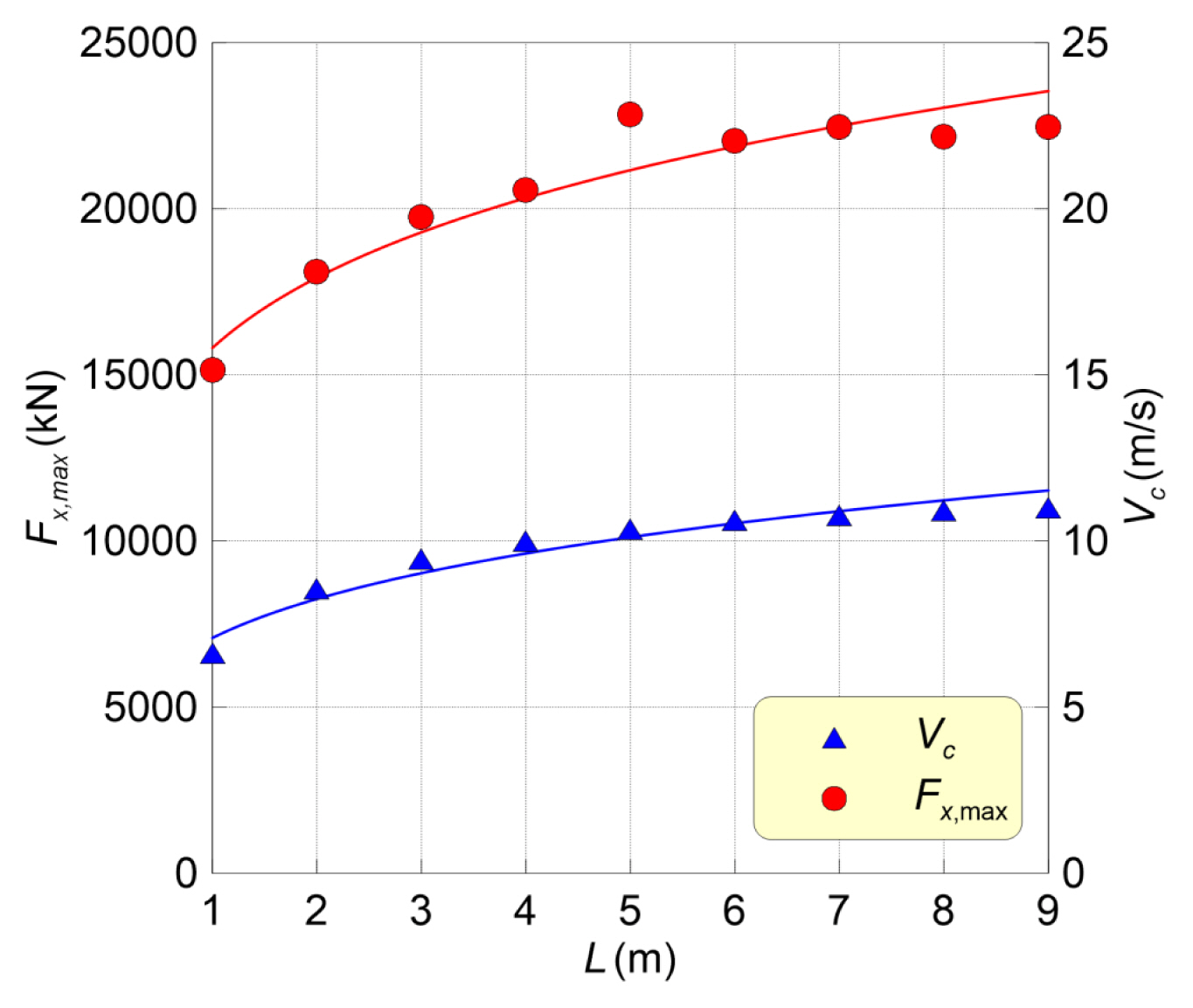
붕괴파에 의한 표류 컨테이너가 기둥과 충돌할 때의 최대 수평력(F_x,max)과 충돌속도(V_c)을 Fig. 16와 Fig. 17에 각각 나타낸다. Fig. 16은 L=9m 조건에서 H 변화, Fig. 17은 H=9m 조건에서 L 변화에 따른 충돌해석 결과이다.

Fig. 16

Maximum collision forces and velocities acting on a column due to the variation of H

Fig. 17

Maximum collision forces and velocities acting on a column due to the variation of L

정지수괴의 L이 9m일 때, H가 증가할수록 컨테이너의 F_x,max 뿐 아니라, V_c 역시 크게 증가하는 경향을 Fig. 16에 잘 나타낸다. H가 클수록 붕괴파의 전파속도가 빠르기 때문에 표류 컨테이너의 이동속도가 증가함과 더불어 기둥과의 충돌력이 커진다. H=9m의 정지수괴에서 L가 클수록 따른 표류 컨테이너의 F_x,max 및 V_c가 큰 경향을 보인다. 이것은 붕괴파의 전파속도와 밀접한 관계가 있다. L≧5m에서 전파속도의 차이가 0.1초 이내이기 때문에 V_c 역시 큰 차이를 나타내지 않는다. 그로 인해 L≧5m에서 F_x,max의 차이가 크게 발생하지 않으며, 충돌면에 따른 차이만 보이고 있다.

3.3.3 최대 충돌하중 비교

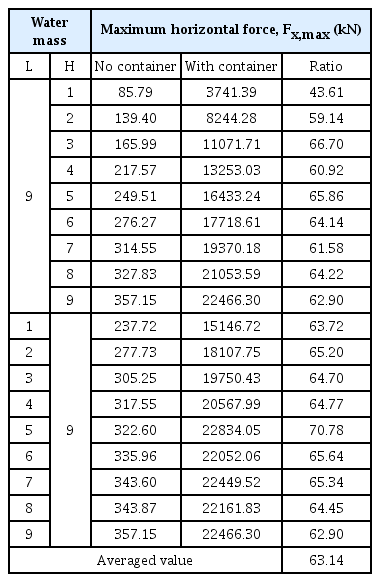
수치수조에서 기둥에 작용하는 붕괴파의 충격력과 표류 컨테이너의 충돌력은 아주 큰 차이를 발생한다. 이것을 비교하기 위해 컨테이너 유무에 따른 기둥에 작용하는 최대 수평력(F_x,max)를 Table 2에 각각 나타낸다.

Table 2

Maximum horizontal force acting on a column

붕괴파가 기둥에 작용하는 충격력보다 만재 컨테이너가 표류해 충돌하는 경우가 최소 43.61배, 최대 70.78배, 평균 63.14배를 나타낸다. 이것은 해일에 충격파에 의한 1차 재해보다 표류 컨테이너 충돌에 의한 2차 재해의 규모가 상당히 크다는 것을 보여주는 것이다.

4. 결론

본 연구에서는 유체-구조 비선형 상호작용을 직접 고려할 수 있는 LS-DYNA를 이용하여 해일에 의한 물체의 유출-표류-충돌 해석의 적용성을 검토하였다. 먼저, LS-DYNA의 타당성 및 유효성을 입증할 목적으로 Kleefsman et al.(2005)의 실험과 비교한 결과, 붕괴파의 수위변화 및 구조물에 작용하는 파압이 잘 일치하였다. 그리고 LS-DYNA에서 수행한 붕괴파에 의한 컨테이너의 유출-표류-충돌 해석의 주요 결과는 다음과 같다.

1) LS-DYNA를 이용해 붕괴파에 의한 컨테이너의 유출표류-충돌 과정을 모의할 수 있었다.

2) 정지수괴의 H가 클수록 붕괴파의 전파속도는 증가하였다. L가 클수록 전파속도가 증가하는 경향을 나타내었으나, L≧5m 조건에서는 큰 차이를 나타내지 않았다.

3) 기둥에 작용하는 붕괴파의 충격력은 전파속도에 빠를수록 처오름 크게 발생하여 큰 값을 나타내었다.

4) 컨테이너가 존재하는 경우, 붕괴파에 의한 표류 및 충돌 속도는 전파속도와 같은 경향을 보였다.

5) 붕괴파에 의한 컨테이너의 유출-표류-충돌에 따른 F_x,max는 정지수괴의 H와 L가 클수록 증가하였다.

6) 붕괴파에 의한 만재 컨테이너의 충돌은 컨테이너가 없는 경우보다 최소 43.61배, 최대 70.78배, 평균 63.14배의 F_x,max를 발생시켰다.

이로써 LS-DYNA는 해일에 의한 물체의 유출-표류-충돌 해석에 적용할 수 있는 하나의 도구가 될 수 있음을 본 연구를 통해 확인하였다. 또한, 해일에 의한 월파/류, 침수, 충격파와 같은 1차 재해뿐만 아니라, 표류물에 의한 2차 재해의 위험성을 확인할 수 있었다.

Acknowledgements

이 성과는 2021년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2021R1A2C4002665).

References

Choi H. 2020;Experimental study on response characteristics of reinforced concrete buildings due to waterborne debris impact loads. Journal of the Korean Recycled Construction Resources Institute 8(4):590–595.

Hwang T, Yeom GS, Seo M, Lee C, Lee WD. 2021;Impact of the thruster jet Flow of ultra-large container ships on the stability of quay walls. Journal of Ocean Engineering and Technology 35(6):403–413.

Kim JH, Baeg DY, Seo JK. 2021;Numerical investigation of residual strength of steel stiffened panel exposed to hydrocarbon fire. Journal of Ocean Engineering and Technology 35(3):203–215.

Kleefsman KMT, Fekken G, Veldman AEP, Iwanowski B, Buchner B. 2005;A volume-of-fluid based simulation method for wave impact problems. Journal of Computational Physics 206(1):363–393.

Ko H, Cox D, Riggs H, Naito C. 2015;Hydraulic experiments on impact force from tsunami-driven debris. Journal of Waterway, Port, Coastal, Ocean Engineering 141(3):04014043.

Kosbab BD. 2010. Seismic performance evaluation of port container cranes allowed to uplift. Ph.D. dissertation Georgia Institute of Technology; USA:

Kumagai K, Oda K, Fujii N. 2006. Applicability of simulation model for drift behavior of containers due to tsunami. In : Proceeding of the Techno-Ocean 2006/19th JASNAOE Ocean Engineering Symposium. Kobe, Japan.

Lee DJ, Shin SB, Kim MH. 2019;Modeling of the temperature-dependent and strain rate-dependent dynamic behavior of glass fiber-reinforced polyurethane foams. Journal of Ocean Engineering and Technology 33(6):547–555.

Lee WD, Jeong YM, Choi KN, Hur DS. 2019;Water wave propagation caused by underwater blasting in a 3d numerical wave tank. Journal of Ocean Engineering and Technology 33(4):364–376.

Madurapperuma MAKM, Wijeyewickrema AC. 2012;Inelastic dynamic analysis of an RC byilding impacted by a tsunami water-borne shipping container. Journal of Earthquake Tsunami 6(1):1250001.

Mase H, Kim S, Hasegawa M, Jeong JH, Yoon JS. 2020;Development of wave overtopping-overflow transition model based on full-scale experiments. Journal of Ocean Engineering and Technology 34(2):128–135.

Mizutani N, Takagi Y, Shiraishi K, Miyajima S, Tomita T. 2005;Study on wave force on a container on apron due to tsunamis and collision force of drifted container. Proceedings of Coastal Engineering, JSCE 52:741–745.

Poehlmann-Martins F, Gabrys J, Souli M. 2005. Hydrodynamic ram analysis of non-exploding projectile impacting water. In : Proceedings of the ASME 2005 Pressure Vessels and Piping Conference. Denver, Colorado, USA. p. 267–273.

Riggs HR, Cox DT, Naito CJ, Kobayashi MH, Pian Aghl P, Ko HT-S, Khowitar E. 2013. Water-driven debris impact force on structures: Experimental and theoretical program. In : Proceeding of the ASME 2013 32nd International Conference on Ocean, Offshore and Artic Engineering. New York, USA.

Santini P, Palmieri D, Marchetti M. 1998. Numerical simulation of fluid-structure interaction in aircraft fuel tanks subjected to hydrodynamic ram penetration. In : 21st the International Council of the Aeronautical Sciences (ICAS) Congress. Melboume, Australia.

Seddon C, Moodie KThyer A, Moatamedi M. 2004;Preliminary analysis of fuel tank impact. International Journal of Crashworthiness 9(3):237–244.

Seo M, Yeom GS, Lee C, Lee WD. 2022;Numerical analyses on the formation, propagation, and deformation of landslide tsunami using LS-DYNA and NWT. Journal of Ocean Engineering and Technology 36(1):11–20.

Souli M, Ouahsine A, Lewin L. 2000;ALE formulation for fluid-structure interaction problems. Computer Methods in Applied Mechanics and Engineering 190(5–7):659–675.

Yeom GS, Mizutani N, Hur DS, Bae KS. 2009. Estimation of collision force of drifted container based on fluid-structure Interaction. In : Proceedings of the Joint Conference of the Korean Association of Ocean Science and Technology Societies. Changwon, Korea.

Yeom GS, Mizutani N, Hur DS, Lee WD. 2017;Application of a modified estimation formula for collision force of deformed drifting containers under tsunami conditions. Journal of Coastal Research 33(3):720–730.

Yeom GS, Nakamura T, Mizutani N. 2009;Collision analysis of container drifted by runup tsunami using drift collision coupled model. Journal of Disaster Research 4(6):441–449.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Gauge	Coordinate
Gauge	x (cm)	y (cm)	z (cm)
H1	−58.2	0	-
H2	100	0	-
P1	116.3	2.6	−52.9
P2	116.3	2.6	−48.9
P3	116.3	2.6	−44.9
P4	116.3	2.6	−40.9
P5	118.4	−2.6	−38.9
P6	122.4	−2.6	−38.9
P7	126.4	−2.6	−38.9
P8	130.4	−2.6	−38.9

Water mass		Maximum horizontal force, F_x_,max (kN)
L	H	No container	With container	Ratio
9	1	85.79	3741.39	43.61
	2	139.40	8244.28	59.14
	3	165.99	11071.71	66.70
	4	217.57	13253.03	60.92
	5	249.51	16433.24	65.86
	6	276.27	17718.61	64.14
	7	314.55	19370.18	61.58
	8	327.83	21053.59	64.22
	9	357.15	22466.30	62.90
1	9	237.72	15146.72	63.72
2		277.73	18107.75	65.20
3		305.25	19750.43	64.70
4		317.55	20567.99	64.77
5		322.60	22834.05	70.78
6		335.96	22052.06	65.64
7		343.60	22449.52	65.34
8		343.87	22161.83	64.45
9		357.15	22466.30	62.90
Averaged value				63.14