마커와 고정형 비전센서를 활용한 항만시설 변위 측정 기법 성능 평가
Performance Evaluation of Displacement Measurement System with Marker and Fixed Vision Sensor on Port Structures
Article information
Trans Abstract
This study focused on the measurement of displacement on port structures with the combination of a marker and a vision sensor installed on the fixed location. The proposed algorithm optimizes the intrinsic parameters of the vision sensor using genetic algorithm and then measures the 6-DOF displacement automatically tracking feature points on the marker extracted through the image process. Experimental studies were carried out by using a general IP camera and a marker including 12 feature points. The distance between the camera and the marker was 10 m. Several types of displacements were induced with the precise motion stage, and the results showed that the measurement errors might be reasonable less than 3.5% in rotation and 4.0% in translation. This system was applied on the lock gate located in Incheon port, which corresponds to Type 1 facilities in Korea. The same camera was fixed at 24 m from the marker and the marker was moved by controlling the precise motion stage. The errors of measurements were less than 1 mm and 0.5 degrees, which were precise and accurate enough to evaluate the displacement in the field considering the present evaluation standard for drift, settlement, and slope on port facilities.
1. 서 론
2030년을 기준으로 공용연수 30년을 초과하는 노후 항만 시설물이 약 50%까지 증가할 것으로 예상되며, 노후화로 인한 시설물의 파손 사례가 함께 증가하면서, 일상 점검 및 유지관리를 통하여 최소 비용으로 안전성 및 사용성을 확보하려는 수요가 증가하고 있다(Min et al., 2022; Yu et al., 2022). ｢시설물의 안전 및 유지관리에 관한 세부지침｣에서는 시설물의 침하, 경사/전도, 활동, 이격거리 등 변위와 관련한 항목을 ‘중요결함’으로 분류하고 있으며, 일정한 기준 값을 초과한 변위(선형, 회전)가 발생한 경우 시설물 안전성을 위협하는 중대한 결함으로 규정하고 있다. 변위는 수년 주기의 정밀안전점검 혹은 정밀안전진단 시에 수준측량 등을 통하여 점검자에 의해 직접 측정⋅기록된다. 그러나 항만시설물 상부에서는 크레인, 컨테이너, 중장비, 중차량 등이 상시 이동하므로 작업자 안전 확보에 어려움이 있으며, 2022년 1월 ｢중대재해처벌법｣이 시행됨에 따라 중대산업재해 발생 시 책임 문제로 인하여 항만시설 점검 및 유지 관리에 대한 운영자의 부담이 증가하였다. 따라서 항만 내 작업자 및 점검자의 안전을 최대한 확보하기 위하여 점검의 무인화⋅자동화를 위한 기술이 다양한 분야에서 개발되고 있으며, 이는 시설물의 거동 및 상태에 대한 시간이력관리를 가능하게 함으로써 결과적으로 시설물의 정량적 데이터 관리 자동화로 귀결된다.
변위 측정 무인화 및 자동화를 위하여 센서를 이용하여 물리량을 측정하여야 한다. 현재 구조물의 변위 측정에 주로 사용되는 장비로는 LVDT(linear variable differential transformer), 가속도계 등 접촉식 센서, LDV(laser doppler vibrometer), GPS(global positioning system) 위성을 이용한 장비 등이 있다(Myung et al., 2011; Jeon et al., 2011). LVDT는 기준점을 선정하기 어려운 항만시설에 대해서는 적용이 어렵다. 가속도계는 측정된 가속도 물리량을 이중적분을 통하여 변위로 변환하는 간접적인 방법에 해당하며, 이로 인하여 신호 이동(drift)로 인한 오차가 적분을 통하여 누적된다는 단점이 있다(Gindy et al., 2008). 또한 신호가 온도 등 환경적인 요인에 의하여 영향을 받기 때문에 신호 처리에 어려움이 존재한다. RTK(real time kinematic)-GPS는 구조물의 처짐 변화 계측에 대한 정확도가 낮고 이중 주파수 RTK-GPS의 경우 고가인데다 넓은 지역을 세밀하게 관측하는 데에 한계가 있다(Jo et al., 2013). LDV는 성능은 뛰어날지라도 변위 측정을 위한 고정점이 필요하고 매우 고가이다(Rothberg et al., 2017).
이와 같이 기존의 변위 계측 장비가 가지는 한계점을 해결하기 위한 방안으로 비접촉식 계측 기법인 영상으로부터 변위를 계측하는 기술과 관련한 연구가 활발히 진행되고 있다. 최근 캠코더, 웹캠 등 비전센서의 성능이 과거에 비하여 비약적으로 향상되었으며, 비전센서로부터 촬영된 영상의 해상도 등 품질이 높아 보다 효율적으로 구조물의 변위를 계측할 수 있게 되었다(Lee et al., 2014) 비전센서를 이용한 변위 계측은 대부분 원거리에 고정⋅설치된 카메라를 사용하여 구조물에 존재하는 2차원 특징점을 관측하고 그 움직임을 계측하여 실제 변위를 예측한다. 비전센서를 통하여 특징점이 포함된 영상을 정확하게 촬영하고 영상 내에서 특징점을 안정적으로 추출하여 변위를 추정하기 위한 다양한 기법들이 제안되었다. Olaszek (1999)은 2개의 십자형 마커를 사용하여 동적 하중이 작용하는 교량의 거동을 측정하는 시스템을 개발하였다. 하나의 마커는 고정된 기준으로 설정하기 위해 교량 외 고정된 위치에 설치하였고, 다른 하나는 변위가 발생하는 교량에 설치하여 계측을 수행하였다. Wahbeh et al. (2003)은 두 개의 붉은색 빛을 발산하는 발광 다이오드(light emitting diodes, LED)가 설치된 판을 교량에 설치하여 이를 특징점으로 활용하여 교량의 변위를 계측하였다. Lee and Shinozuka (2006)는 검은색 배경을 가진 4개의 흰색 점을 비대칭 십자형으로 배열한 마커를 사용하여 변위 측정 시스템을 구성하였다. Ji and Chang (2008)은 구조물의 선형적인 부분을 마커로 사용하여 스테레오 비전을 활용해 변위를 측정하는 기법을 제안하였다. Park et al. (2010)는 검은색 배경에 십자형으로 배치된 4개의 흰색 점을 마커로 사용하여 분할 촬영을 통해 대형 구조물을 분할 촬영하여 변위를 계측할 수 있는 기법을 제안하였다. Ribeiro et al. (2014)은 네 개의 흰색⋅검은색 사각형과 5mm의 균일한 포인트들로 이루어진 타겟 패널에 IR 백열등 및 LED를 적용하여 구조물의 변위를 측정하는 기법을 연구하였다. Wu et al. (2014)은 구조물에 캘리브레이션 보드(calibration board)와 균일한 간격의 LED 마커를 부착하여 실제 진동대 위에서 구조물의 움직임을 모니터링하였다. Feng and Feng (2016)은 흰색⋅검은색의 불규칙한 패턴 패널을 실제 구조물의 타겟 근처에 부착하여 비전센서로 패널과 실제 타켓을 추적하는 방법을 비교하였다. Hoskere et al. (2019)는 ArUco 마커를 구조물에 설치하고 마커를 자동 검출하는 알고리즘을 통해 영상 속 구조물의 주기와 모드형상 도출 방법을 연구하였다. 이와 같이 평면형 마커를 구조물에 설치한 다음 마커까지의 가시거리를 확보할 수 있도록 설치한 비전 센서로부터 구조물의 움직임을 정밀하게 측정할 수 있는 다양한 기술이 개발되고 있으며, 이로부터 기존의 고가의 센서 혹은 장비 대신 오로지 마커와 비전센서를 사용하여 비교적 단순하게 변위를 계측할 수 있다.
그러나 실제 항만시설물에서는 이와 같은 영상 변위 측정과 관련한 연구 결과가 보고된 적이 없다. 대다수 연구가 교량을 대상으로 한 변위 추정 기술 개발로 진행되었기 때문에 본 논문에서는 교량과는 다른 운영 환경 및 특징을 가지는 항만시설물을 대상으로 비전센서를 활용한 영상 변위 추정 기술을 개발하고자 하였다. ｢시설물의 안전 및 유지관리에 관한 세부지침｣에서 제시하고 있는 침하, 활동의 평가기준을 살펴보면, 진행성의 경우 a등급은 2cm 미만, b등급은 2~5cm, c등급은 5~8cm, d등급은 8~12cm, e등급은 12cm이상으로 제시하고 있다. 12cm 이상의 경우 침하의 정도가 아주 심하고 광범위하게 발생하여 구조적인 안정을 상실할 수 있는 위험한 상태라고 기술하였다. 경사/전도의 평가기준을 살펴보면, 진행성의 경우 a등급은 1% 미만, b등급은 1~2%, c등급은 2~3%, d등급은 3~4%, e등급은 4% 이상이다. 한편, ｢항만 및 어항 설계기준 내진편(KDS 64 17 00)｣ 에서 제시하고 있는 내진설계 수행 시의 허용변위를 살펴보면, 공용의 관점에서 본 안벽 변형량의 허용값은 중력식 계선안의 경우 수심에 따라 20~30cm이며, 경사는 3~5°이다. 에이프런의 경우 에이프런상의 단차는 3~10cm, 에이프런과 배우부지의 단차는 30~70cm 수준이다. 즉 항만구조물에서 허용 가능한 변위가 수 cm, 수 ° 수준으로 타 시설물 대비 크기 때문에 고가의 고정밀 변위 측정 장비보다는, 수 mm 단위의 촬영 오차가 있을지라도 평면형 마커와 비전센서를 활용한 변위 측정이 보다 효과적일 것으로 판단된다.
본 논문에서는 항만시설물의 효과적인 변위 측정을 위하여 평면 마커와 원거리 고정점에 설치된 비전센서를 이용하여 호모그래피 변환(homography transformation)에 기반한 선형 및 회전 변위(6자유도) 측정 기술을 제안한다. 측정 변위의 정밀도를 향상시키기 위하여 카메라 내부 파라미터를 최적화하기 위한 유전 알고리즘(genetic algorithm)을 개발하고, 이후 고정 위치에서의 연속적인 영상 촬영을 통하여 6자유도 변위의 연속적인 측정이 가능하도록 하였다. 정밀 제어가 가능한 모션 스테이지에 임의 변위를 인가함으로써 변위 측정의 정확도를 평가할 수 있으며, 실제 항만시설물에 마커를 설치하여 실시간으로 변위를 측정하여 인가된 변위 값과 비교하였다. 제안 알고리즘은 추후 다수개의 모듈로 확장하여 항만시설물에 설치된 카메라 등을 활용한 변위 모니터링 시스템으로 활용할 수 있을 것으로 기대한다.
2. 호모그래피를 활용한 선형 및 회전 변위 계측 알고리즘
두 지점 사이의 상대적인 6-자유도 선형 및 회전 변위는 실제 좌표계(world coordinate system) 상의 특징점의 위치와 비전센서의 내부(intrinsic) 파라미터를 이용하여 추정한다. 내부 파라미터는 초점 거리, 주점 및 왜곡 계수를 포함하며 이는 카메라 렌즈의 광학적 특성을 나타낸다. Fig. 1은 실제 좌표계와 영상 좌표계의 특징점을 나타내며, 그림에서 Qi = [X Y Z 1]T (i = 1,…,N)와 qi = [u v 1]T는 각각 실제 및 영상 좌표계의 대응점이다. 이 때, N은 특징 점의 개수이며, 두 좌표계 사이의 관계는 Eq. (1)~(4)로 표현된다.
Homogeneous transformation between world and image planes
위 식에서 fu와 fv는 각 축의 초점 거리를, cu와 cv는 주점을, 그리고 K1, K2, K3, K4는 왜곡 계수이다. r 및 t는 회전행렬 및 선형 벡터를 의미한다. 비전센서의 내부 파라미터 추정을 위하여 본 논문에서는 체커보드와 Lomonosov Moscow State University의 Graphics & Media Lab.에서 개발한 GML 카메라 캘리브레이션 툴박스를 사용하였다. 동일한 평면을 서로 다른 카메라 위치 혹은 방향에서 촬영하고, 각 영상에서의 특징점의 위치를 바탕으로 Eq. (5)로부터 호모그래피행렬인 H를 계산한다. 여기에서
변위 계측의 정밀도를 향상시키기 위하여 유전 알고리즘 기반 카메라 내부 파라미터 최적화 알고리즘을 개발하였다(Karray et al., 2004). 촬영된 체커보드의 영상 품질 등으로 인하여 발생할 수 있는 내부 파라미터의 오차를 보정하기 위하여 계산된 오차 범위 내에서 두 지점 사이의 변위 값을 기반으로 파라미터를 추정하였으며 의사(pseudo) 알고리즘은 Table 1과 같다. Fig. 2의 다양한 크기의 체커보드를 이용하여 내부 파라미터의 초기값을 계측하고, 이를 바탕으로 유전 알고리즘 최적화를 수행한다.
Psuedo code for optimization of intrinsic parameters by using genetic algorithm
Various checkerboards for optimization of intrinsic parameters
3. 실내실험 및 검증
3.1 내부 파라미터 최적화 알고리즘 성능 검증 실험
본 논문에서 제안한 유전 알고리즘을 이용한 내부 파라미터 최적화 알고리즘의 성능 검증을 위하여 실내실험을 수행하였다. 본 연구에서 사용한 영상 기반 변위 계측 시스템은 단순하게 마커와 촬영용 카메라, PC로 구성된다. 비전센서로부터 2m 거리에 Fig. 2의 체커보드를 위치시킨 다음 촬영을 수행하였다. 여기에서, 마커의 정밀한 변위값을 확보하기 위하여 선형 130 µm , 회전 ±0.2° 정밀도를 가지는 Thorlabs사 모션 스테이지(PT1.M-Z8, MLJ150/M, KPRMTE/M) 상에 체커보드를 위치시켰으며, 실제로 마커에 인가되는 변위 값을 실시간으로 PC로 전송하여 수령하도록 하였다. 촬영을 위한 카메라는 줌 기능을 가진 한화테크윈 사의 IP 카메라(XNZ-L6320)를 사용하였다.
실험은 총 3가지의 시나리오로 구성하여 진행하였다: (1) x축 방향으로 -10 mm 이동한 경우, (2) y축에 대하여 5° 회전한 경우, (3) z축 방향으로 -30mm 이동한 경우이다. 각 시나리오에 대하여 10개의 서로 다른 유전 알고리즘 파라미터에 대한 평균 제곱근 오차(root mean square error)를 유전 알고리즘 최적화 전과 후로 나누어 Table 2에 나타내었다. 유전 알고리즘을 적용하여 내부 파라미터를 산출하고, 이를 바탕으로 6자유도 변위를 예측한 경우, 1번 시나리오에 대하여 RMSE가 선형변위에 대하여 28%, 회전변위에 대하여 61% 감소하였으며, 2번 시나리오에서는 각각 11%, 40%, 3번 시나리오에서는 32%, 31% 감소하였다. 즉, 유전 알고리즘 기반 내부 파라미터 최적화 알고리즘을 통하여 최대 60%까지 RMSE 오차를 감소시킬 수 있음을 확인하였다.
The results of 6-DOF displacement with and without using genetic algorithm (RMSE: Root mean square error)
3.2 6자유도 측정 알고리즘 성능 검증 실험
항만구조물에서 카메라와 마커 사이의 거리는 최소 10 m 이상이다. 카메라와 마커 사이의 거리는 촬영 영상의 해상도와 밀접한 관련이 있으며. 한 픽셀의 크기가 오차 크기를 좌우한다. 따라서 실 구조물에서의 개발 알고리즘 검증 실험에 앞서 실내실험을 수행하였다. 평면형 마커와 카메라 사이의 거리를 10 m로 설정하여 측정 영상 변위의 오차를 검토하였다. 앞선 내부 파라미터 최적화 알고리즘 검증 실험과 동일한 형태로 영상 기반 변위 계측 시스템을 구성하였다. 마커는 다수개의 특징점이 포함된 사각 또는 삼각형을 이용하여 Fig. 3(a)와 같이 설계하였으며, 최외곽 크기는 150×150 mm이다. 그림 내 좌표값의 단위는 mm이며, 두 쌍의 직사각형 및 외부의 정사각형 코너점을 이용하여 총 12개의 특징점을 가지고 있다. 이와 같이 다수의 도형을 포함함으로써 복수개의 항만구조물에 다수의 마커를 부착하여 촬영하는 경우에 각 위치를 구별하기 위한 식별자로 사용할 수 있으므로 관리에 용이하다는 장점이 있다. 카메라와 PC는 이더넷 통신으로 연결하여 제어하도록 하였다(Fig. 3(b)).
Experimental setup for validation of the proposed 6-DOF measurement algorithm. (a) Marker design with 12 feature points and (b) experimental setup
실험은 선형 및 회전 변위를 계측할 수 있는 시나리오로 구성하여 진행하였다: (1) y축에 대하여 ± 20° 회전한 경우(yaw), (2) y축 방향으로 25 mm 이동한 경우이다. 마커를 촬영한 영상은 (1) 영상 왜곡 보정, (2) RGB 채널 분리, (3) 이진화, (4) 흑백 반전, (5) 외곽선 검출, (6) 코너 검출의 프로세스를 통하여 특징점의 위치정보를 추출하며, 호모그래피 변환을 통하여 실제 좌표계에서의 선형 및 회전 변위를 계측한다.
Fig. 4는 비전센서로부터 계측한 선형 및 회전 변위를 실제 인가된 변위 값(ground of truth)과 비교한 결과이다. 인가된 변위와의 오차를 비교한 결과, 선형 및 회전 변위의 RMSE 값을 Table 3에 나타내었다. 회전 변위에 대한 오차는 20°를 기준으로 약 0.7° 이내로 약 3.5%였으며, 선형 변위에 대한 오차는 Y축의 경우 0.8mm 이내로, 4% 수준이었다. 비전센서 및 특징점을 기반으로 하는 변위 계측에 있어, 특징점이 오검출 되는 경우 Fig. 4(a)에서 나타나는 바와 같이 변위 계측 중 값이 튀는 현상이 발생한다. 이는 향후, 관성항법장치(IMU: intertial measurement unit)와 같은 센서 융합을 통해 필터링함으로써 개선시킬 수 있다(Jeon et al., 2022).
Experimental results of (a) translational and (b) rotational displacement measurements by using a vision sensor
RMSE of translational and rotational displacements
4. 현장실험 및 검증
4.1 대상 시설물
항만시설은 1장에서 언급하였듯이 침하, 경사/전도, 활동, 케이슨⋅블록 이격거리와 같이 변위와 관련한 점검항목의 관리가 시설물의 안전성 및 사용성 측면에서 매우 중요하게 다루어진다. 이 중에서 본체가 전면 혹은 후면으로 이동하는 활동의 경우 영상 촬영 방향으로의 발생 변위에 해당하여 비전센서 기반 변위 측정 시스템의 직접적인 적용이 어려운 반면, 침하 혹은 경사/전도의 경우에는 측정 및 모니터링이 가능하다.
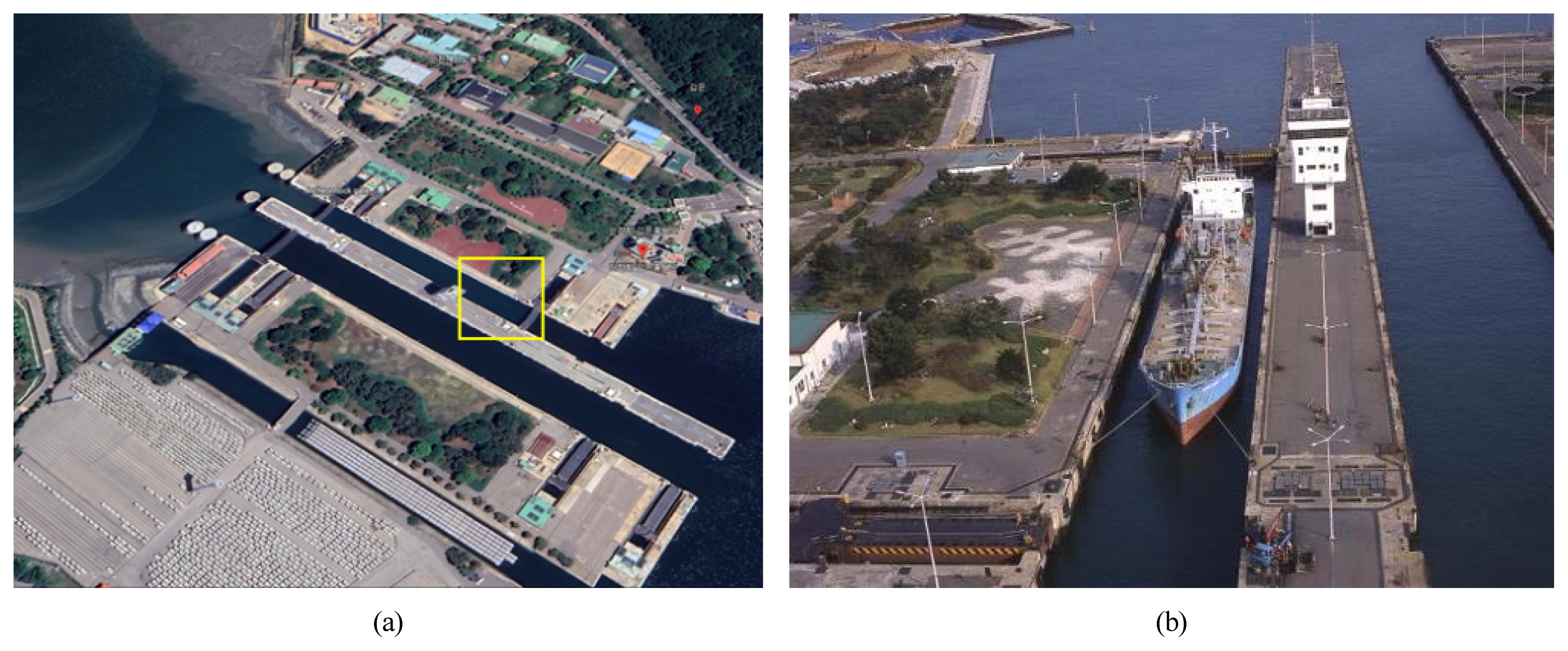
본 논문에서 제안된 기술을 현장실험을 통해 검증하기 위하여, 변위 모니터링이 필수적으로 필요한 인천항 갑문을 대상지로 선정하였다. 인천항 갑문은 최대 10m 수준의 조수 간만의 차를 극복하고 인천항 내항에 접안하는 선박의 안정적인 통항 및 접안⋅하역을 지원하기 위하여 1974년 준공된 대표적인 1종 시설물이다. 그러나 갑문이 노후화됨에 따라 운영 효율이 저하되고 유지보수 난이도가 높아짐에 따라, 인천항만공사는 갑문의 유지관리 및 운영 업무의 효율성을 향상시키기 위하여 2017년부터 스마트 갑문 구축을 추진하였다. 추진 내용에는 변위 모니터링 시스템도 포함된다. 인천항 갑문에는 Fig. 5(a)와 같이 1만톤급(우측) 및 5만톤급(좌측) 취배수문 2기가 있으며, 수문의 계폐를 통하여 Fig. 5(b)와 같이 선박이 통항한다. 스마트 관리를 위하여 구축된 혹은 예정인 스마트 안전장비로는, 안전고리체결 스피커, CCTV, 에너지 저장 장치, 수위관측장치, 모터진동센서, 장력센서, 갑문 변위측정시스템 등이 있다. 갑문은 국가에서 지정한 보안시설에 해당하여 영상 촬영 및 공개 등이 불가하기에, Fig. 5는 기 보도된 영상 자료를 활용하였다.
Target structure for validation of the proposed algorithm (a) satellite photograph (from Google Earth) (b) aerial photograph (from Yonhap News Agency)
4.2 실험 개요
고정형 영상과 마커를 이용한 변위 추정 알고리즘의 성능을 검증하기 위하여 Fig. 6과 같이 육상 측에 네트워크 카메라를, 1만톤급 취배수문 측에 마커를 설치하였다. 카메라와 마커 사이의 거리는 24m이다. 인위적으로 마커에 선형 및 회전 변위를 인가하기 위하여 마커는 Fig. 6과 같이 3축 선형변위(X,Y,Z) 및 Z축 중심 회전변위(yaw) 제어가 가능한 모션 스테이지에 마커를 고정하였다. 마커의 크기는 카메라와 마커 사이의 거리 및 목표 해상도를 고려하여 450×450mm로 제작하였다. 촬영을 위한 카메라는 실내실험과 동일하게 한화테크윈 사의 IP 카메라(XNZ-L6320)를 사용하였다. 본 논문에서 제안하는 시스템은 단일 마커와 고정 설치가 가능한 카메라만을 사용하여 마커 위치에서의 6자유도 변위를 측정하는 것으로, 기존 토탈스테이션 등 측량장비(예: NTS-332R6)와 비교하면 그 비용이 20% 수준으로 감소할 뿐만 아니라 실시간 자동화 계측이 가능하다는 장점이 있다.
Experimental setup in the field
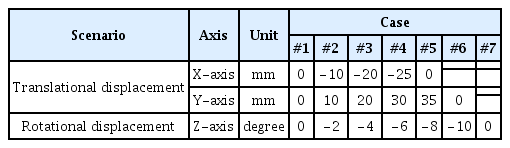
마커에 인가되는 변위 시나리오는 Table 4와 같다. 변위 계측의 축 방향은 다음과 같다: 갑문의 처짐(+Y 방향), 외해방향 수평변위(+X 방향), 외해 방향 경사(R 방향). 기존 세부지침 상의 평가기준 ‘a’ (진행성 기준 최대 범위: 5cm)를 고려하여 인가 변위를 5~10mm, 2° 단위로 하였으며, X축 최대 -25mm까지, y축 최대 35mm까지, z축 중심 회전 변위 최대 10도로 설정하였다.
Displacement control scenarios for validation in the field
4.3 실험 결과 및 분석
특징점의 실제 및 영상 좌표계 사이의 관계식을 이용하여 두 지점 사이의 상대적인 6자유도 변위 계측을 수행하였으며, 그 과정을 Fig. 7에 나타내었다. 비전센서를 이용하여 원거리 마커를 포함한 영상을 획득하고, 획득된 영상 내 렌즈의 왜곡을 보정한 뒤, 흑백으로 변환한 다음 특징점을 추출한다. 이 모든 것이 비전센서를 제어하는 PC에 탑재되어 있어 일련의 과정이 자동으로 이루어진다. Fig. 7은 촬영한 영상으로부터 특징점을 추출하는 과정을 단계별로 나타낸 그림이다.
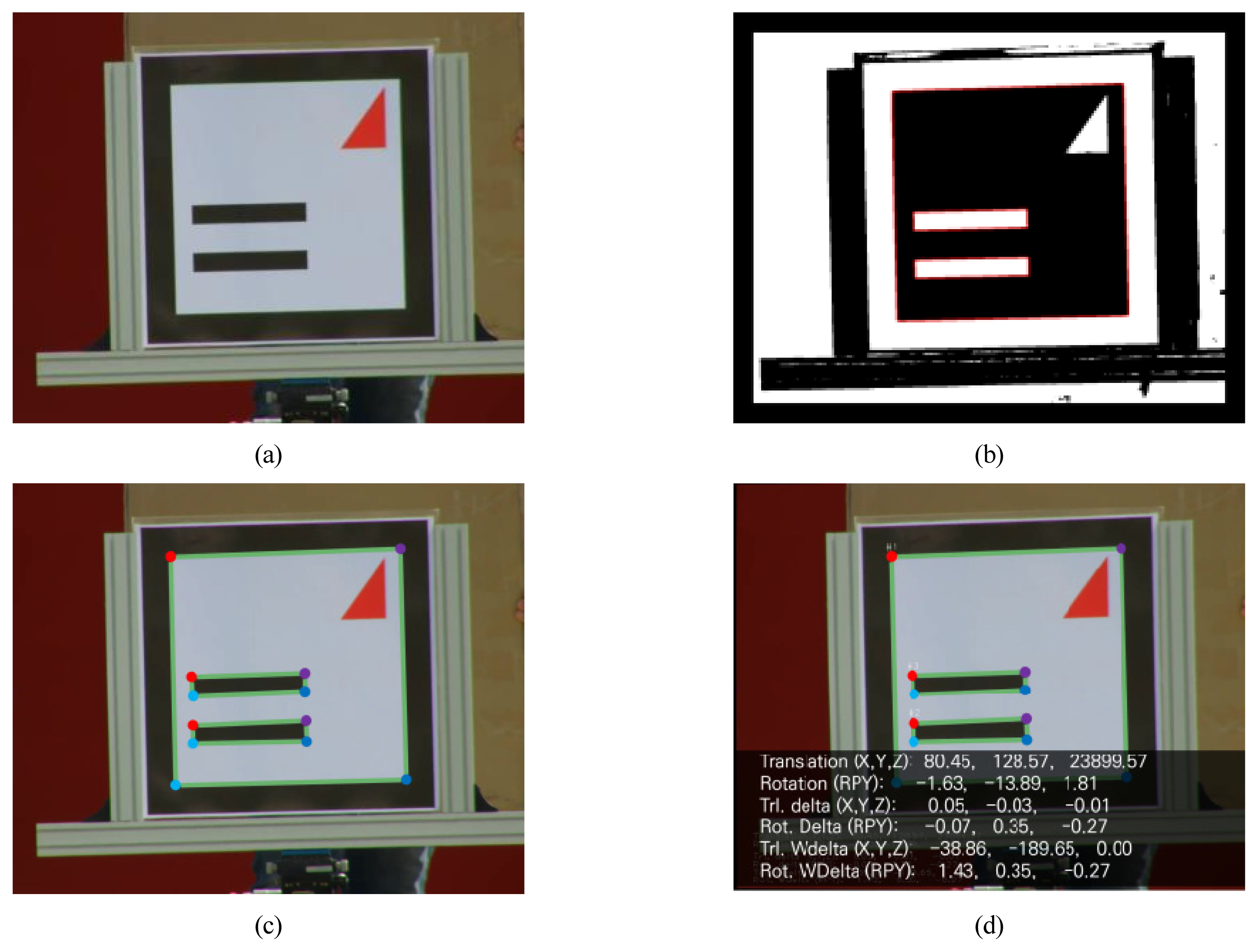
Image processing for real-time 6-DOF displacement measurement (a) original image, (b) contour detection, (c) corner detection, and (d) 6-DOF measurement
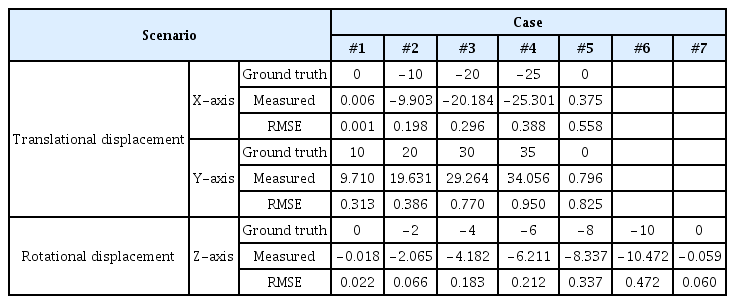
Table 4의 시나리오에 대하여 비전센서로부터 측정한 선형 및 회전 변위를 Fig. 8에 구분하여 나타내었다. Fig. 8(a)에서 x축 방향으로 선형 변위가 인가될 때 y축, z축 변위 및 회전 변위는 ±1mm 이하, ±1° 이하의 오차값을 가지는 것으로 측정되었으며, x축 변위는 인가된 변위와 약 1mm 오차로 정확하게 추정함을 확인할 수 있었다. Fig. 8(b)는 y축 방향으로 선형 변위가 인가되는 경우로, 촬영 방향인 z축에 대해서는 약 8mm의 오차가 발생하였으나, 나머지에 대해서는 ±1mm 이하, ±1° 이하 오차를 보여주었다. 선형 변위가 인가된 y축에 대해서는 변위가 인가되는 시점에서만 최대 2mm 수준의 오차를 보여주었으며 변위 인가 종료시점에는 1mm 이하의 오차로 정확하게 추정함을 알 수 있다. Fig. 8(c)는 z축을 중심으로 회전변위(yaw)가 인가되어 갑문의 길이(내해) 방향으로 기울어진 경우이다. 모션 스테이지를 통하여 회전변위만 인가하였으나, x축 및 y축에 대한 변위가 함께 나타났다. 이는 마커의 중심점을 기준으로 회전한 것이 아니라 마커의 하단 중심부를 기준으로 회전하였기 때문에 선형 변위가 함께 발생한 것이며 y축에 대해서는 일부 오차가 발생하였다. 그래프에서의 인가된 회전 변위 참값(ground truth)은 원점을 보정하여 계산한 값에 해당한다. 선형 변위 인가 시와 마찬가지로, 회전 변위 역시 매우 정확하게 측정됨을 알 수 있으며, 오차는 0에 가까웠다. Roll과 Pitch의 경우 ±1° 이하의 오차를 보여주었다.
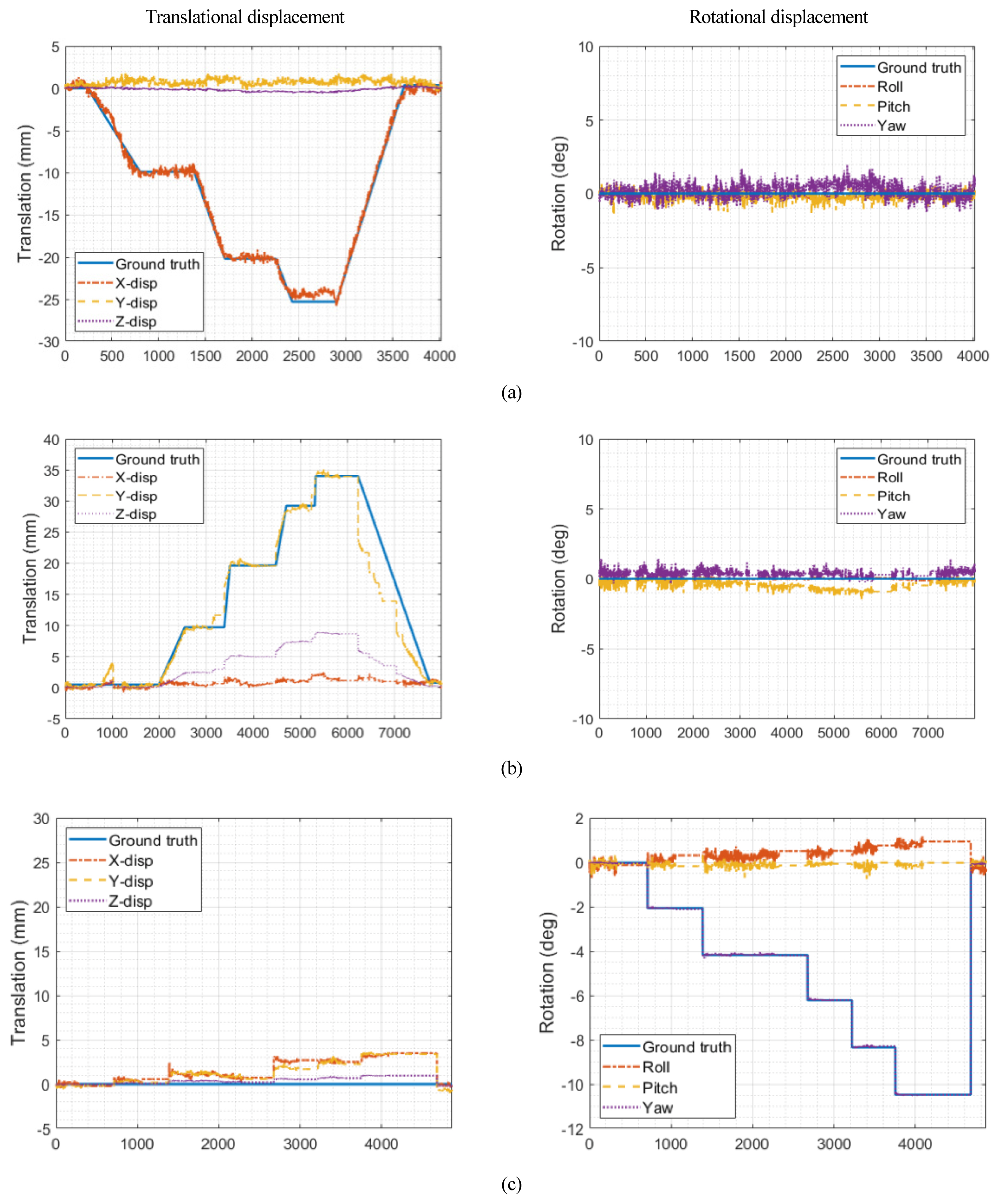
Field validation results of vision-based measurements (a) translation along x-axis, (b) translation along y-axis, and (c) rotation around z-axis
Table 5는 각 시나리오에 대하여 RMSE 값을 표시한 것이다. X축 선형 변위가 인가되었을 때 25mm 인가변위에 대하여 약 0.388mm RMSE 값을 가지며 이는 인가된 변위 대비 약 2% 오차를 의미한다. y축 선형 변위 인가시에도 마찬가지로 약 2~3% 오차가 발생하였다. z축 중심 회전 변위 인가 시에는 RMSE 값이 0.5° 이하였다. 즉, 실제 항만시설에서 비전센서로부터 측정된 영상으로 변위를 측정하였을 때 RMSE 값이 1mm, 0.5° 미만이었으며, 실제 항만시설의 안전성 및 사용성에 영향을 미치는 변위가 수 cm임을 고려할 때 허용 가능한 수준의 계측 오차임을 알 수 있다. 이로부터 갑문 등 항만시설에서 비전센서를 통하여 변위 모니터링을 충분히 수행할 수 있다는 가능성을 확인하였으며, 추후 관성항법장치 등을 포함한 센서 융합 기술을 통하여 정밀도를 더욱 향상시킬 수 있을 것이다.
RMSE of measured displacement in the field
5. 결 론
본 논문에서는 비전센서와 평면형 마커로 구성된 변위 계측 알고리즘을 개발하였으며, 실제 항만시설에서의 적용 가능성을 검토하였다. 개발 알고리즘은 우선 유전 알고리즘을 통하여 카메라 내부 파라미터를 최적화한 다음 마커의 특이점을 추출하여 6자유도를 측정하는 것으로, 마커(150×150mm)가 설치된 구조물의 변위를 실시간으로 측정할 수 있다. 개발 알고리즘의 검증을 위하여, 선형 및 회전 변위의 정밀한 제어가 가능한 모션 스테이지에 마커를 고정시킨 다음 변위를 인가하였으며, 마커에서 10m 떨어진 네트워크 줌 카메라를 이용하여 마커를 촬영하였다. 그 결과 회전 변위에 대한 오차는 3.5%, 선형 변위에 대한 오차는 4.0%였다. 개발 알고리즘의 현장 적용성 검토를 위하여 항만시설 중 1종 시설물에 해당하는 인천항 갑문에서 실험을 수행하였다. 마커와 비전센서 사이의 거리가 24m에 해당하여 마커의 크기를 450×450mm로 증가시켰으며, 수평변위 및 처짐, 기울임을 모사하기 위한 변위를 모션 스케이지를 활용하여 마커에 인가하였다. 계측 결과 오차가 1mm, 0.5° 미만으로 ｢시설물의 안전 및 유지관리에 관한 세부지침｣ 상 변위에 대한 평가기준을 고려할 때 충분한 정밀도 및 정확도를 확보하였다. 향후 다수개의 센서 모듈로 확장하기 위하여 마커 및 비전센서 기반 비접촉 무인 변위 모니터링 하드웨어 플랫폼을 개발하고자 한다. 이때 줌 기능이 강화된 비전센서를 사용함으로써, 원거리에서 보다 작은 크기의 마커를 탐지하고 두 지점 사이의 6자유도 변위를 안정적으로 계측할 수 있을 것으로 기대한다.
감사의 글
본 논문은 해양수산부 재원 해양수산과학기술진흥원(과제번호: 20210659) 및 산업통상자원부 재원 한국산업기술평가관리원(과제번호: 20011780)의 지원을 받아 수행되었으며, 이에 감사드립니다. 또한 항 내 시설물 촬영 및 지원에 협조해주신 인천항만공사와 방유석 대표에게 감사드립니다.