선박주묘에 의한 풀루크 앵커의 침투깊이 산정을 위한 수치해석
Numerical Analysis for Estimating Penetration Depth by Ship-dragged Fluke Anchor
Article information
Trans Abstract
Anchor penetration by ship anchoring is emerging as a major risk factor for submarine cable. A numerical analysis method was established to predict the anchor penetration depth by ship-dragged fluke anchor in relation to setting the optimal burial depth of submarine cable. The soil resisting forces (bearing force, friction force) generated during the anchor penetration process were calculated for each of the fluke, shank and mooring chain of the anchor. The results of the numerical analysis were compared with the existing chart values of Vryhof (2015). It was found that it is desirable to use the force coefficients of strip foundation for the fluke and shank, and the force coefficients of a single vertical pile for mooring chain. The numerical analysis well reproduced the penetration trajectory in which the inclination angle of the lower surface of fluke gradually converged to zero.
1. 서 론
전력송전과 통신을 위하여 바다에 설치되는 해저케이블은 다수의 자연적 또는 인위적 위해인자에 의하여 손상될 가능성이 있다. 최근 2022년도 1월에 발생한 남태평양 통가 해저지진에서도 해저 통신케이블 손상으로 인하여 상황대처 및 복구에 많은 불편이 초래된 바 있다 (The New York Times, 2021). 또한, GCube Insurance (2021)는 해상풍력발전 부문에서 과거 2010-2020의 십 년 동안 발생한 손해보험 신청 중 해저케이블 관련 부분이 전체 30%로, 그리고 누적 보험지급액이 전체 50% 이상 차지한 것으로 보고한 바 있다. 따라서, 해저케이블을 다수의 위해인자로부터 보호하는 것은 해저케이블의 경제성 유지 측면에서 매우 중요하며 적절한 보호공을 처음부터 잘 강구할 필요가 있다.
1980년대 초기부터 해저케이블을 매설하기 시작하면서 어구사용 등에 대한 피해 (ICPC, 2009)가 현저히 감소한 반면, 대신 선박앵커 주묘가 새로운 케이블 피해원인으로 지목되고 있다 (CIGRE, 2009). 따라서, 전체적인 케이블 포설의 경제성을 유지하면서 동시에 주묘 피해를 방지하기 위한 적정 매설심도의 결정이 중요한 설계 현안문제로 부각되고 있다. 국내에서는 완도-제주 간 제3연계선 (KEPCO, 2019)을 포함한 다수의 해저케이블 포설사업에서 실증 및 모형실험과 경험에 바탕을 둔 매설심도 결정방법들이 사용되어 왔다. 그러나 소정 중량의 선박을 이용하여 일부 해역에서 수행한 실증실험이 전 해저케이블 노선의 상황을 충분히 대표한다고 보는 것은 무리가 있다. 그리고 모형실험 역시 대부분 1g 실험으로 수행되었으나 상사율 오차에 대한 보정이 포함되어 있지 않다. 경험적 방법 역시 기존 해저케이블들의 매설심도를 참고하는 식으로 되어 있어 이 역시 정확한 매설심도 산정방법으로 보기는 어렵다.
국외의 경우는 Allan (1998)이 제시한 BPI (Burial Protection Index) 방법과 그리고 Carbon Trust (2015)가 제시한 CBRA (Cable Burial Risk Analysis) 방법이 있으나 이들 역시 아직은 정성적인 수준을 벗어나지 못하고 있는 실정이다. 앵커침투는 앵커의 형상 및 중량, 해저지반의 토질특성에 따라 달라지며, BPI 방법은 Fig. 1에서 볼 수 있듯이 앵커중량 및 어구사용에 따라 정해지는 BPI와 그리고 토질의 지지력 특성을 고려하여 매설심도를 구하는 방식이다. 그러나, 본연적으로 이 방법은 BPI와 토질의 지지력 특성을 정성적으로 판단해야 하는 문제점을 내포하고 있다. 한편, CBRA 방법은 선박 사고확률에 입각하여 매설심도를 재현주기별로 산정하는 것이다. 결과로서 제시되는 천년 이상의 재현주기가 설계 실무적 관점에서 볼 때 과연 어느 정도의 현실성을 갖는가 하는 논란도 충분히 있을 수 있지만 가장 중요한 선박 DWT와 주묘 침투 깊이 간 정량적 관계설정이 기법에 포함되어 있지 않다.
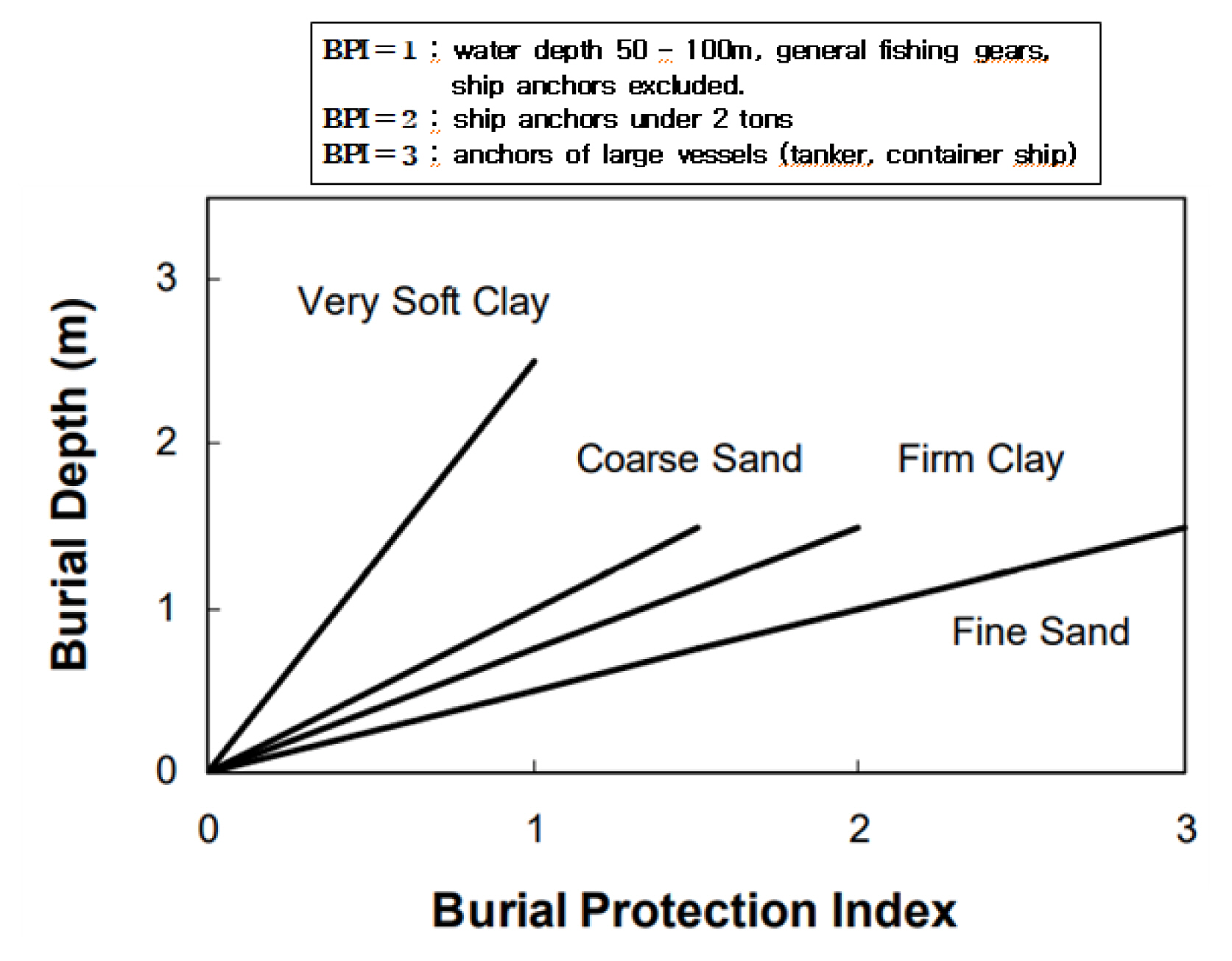
BPI Method for estimating burial depth of drag anchor (adapted from Allan 1998)
상기와 같이 선박 주묘에 대한 매설심도를 정확히 설정하기 위해서는 우선 주묘에 의한 앵커의 지반 침투깊이를 정확히 산정하여야 한다. 사실 앵커의 침투깊이 산정은 꽤 오랜 역사를 가지고 있으며, 대별하면, 실험적 방법과 해석적 방법이 있다. 먼저 실험적 방법으로서 NCEL (1984)은 실해역 관측에 근거하여 여러 형태의 앵커에 대해서 파주력과 침투깊이를 산정할 수 있는 도표를 제시하였다. 그러나 주로 앵커의 파주력에 대한 결과에 치중하였으며, 여러 앵커 유형에 대하여 침투깊이-견인거리 (drag distance)의 관계에 대해서는 다소 정성적인 도표를 제시하였다. 한편, Vryhof (2015)는 여러 종류의 앵커에 대하여 비교적 상세한 기하학적 제원과 함께 점토와 사질토 각각에 대하여 극한파주력, 침투 깊이 그리고 견인거리를 독취할 수 있는 도표를 제시하였다. 이 도표는 기존의 여러 실증 및 모형실험결과에 근거를 둔 것으로 판단되며, 많은 앵커 주묘 관련 문헌에서 비교자료로 사용되어왔다. 그러나, 도표들이 주로 1톤 이상의 대형 앵커들을 대상으로 작성되었기 때문에 연안역에서의 소형선박들에 적용하는 것은 한계가 있다.
해석적 방법은 한계평형법 (Limit equilibrium method), 소성한계법 (Plastic limit method) 그리고 토체저항법 (Soil resistance method)으로 구분할 수 있다. 한계평형법은 Nam, et al. (2019), Thorn (1998), Neubecker and Randolph (1996), 그리고 Tabatabaee (1981) 등에 의하여 제시되었으며 앵커 주변 토체에 파괴면을 설정하고 앵커의 주묘과정 중 파괴면에서 발생하는 저항력과 앵커에 작용하는 수동토압들간의 역학적 평형관계를 해석하는 방법이다. 그러나, 한계평형법은 일반적으로 부정정 문제로서 (Rahardjo and Fredlund, 1984), 해석의 폐합 (closure)을 달성하기 위한 여러 가정이 포함되어 있는 점, 특히 앵커에 작용하는 각 힘들의 작용점을 정확히 설정하기가 매우 어려운 점 등은 설계실무에서의 사용성을 저하시키는 주요 소인이 될 수 있다. 소성한계법은 토체를 완전한 소성체로 보고 해석하는 방법으로서 당연히 점토질 토체에 대해서만 적용 가능하다 (O’Neill, et al., 2003; Aubeny and Chi, 2010; Wang, et al., 2014). 이와 같이 상기 두 방법은 각각 사질토와 점토질에 대해서 선별적으로 적용 가능하나 이 두 토질조건에 대한 해석개념이 출발부터 완전히 다르기 때문에 점토에서의 주묘와 사질토에서의 주묘를 동등한 기준으로 일관성 있게 해석하는 것이 매우 어렵다. 경우에 따라서는 일반적 기대와는 달리 사질토 조건이 점토질 조건보다 침투깊이가 더 크게 발생 발생할 수 있다.
마지막으로 토체저항법은 말뚝침투 해석과 유사하며 주묘 과정 중 앵커표면에 발생하는 흙의 저항력을 지지력 (bearing force)과 마찰력 (friction force)으로 구분하여 해석하는 방법이다. DnV-RP-E302 (2002, p. 26)에서도 앵커주묘는 실질적으로 말뚝 설치와 유사하다는 점을 지적한 바 있다. 말뚝 설치에서는 점토질과 사질토 각각에 대하여 지지력과 마찰력을 달리 결정할 뿐 해석방법은 근본적으로 동일하기 때문에 상기와 같이 기본개념이 완전히 다른 모델들을 적용하면서 발생하는 비일관성 문제를 원천적으로 극복할 수 있다. Neubecker and Randolph (1995)는 점토질 토양에 대하여 본 방법을 적용하여 복합 토층에서의 앵커궤적과 최대침투깊이 (UED, ultimate embedment depth)를 계산할 수 있는 수식을 전개하였다. 그 이후 Liu et al. (2010)은 본 방법을 확장하여 점성토와 사질토 각각에 대하여 최대침투깊이를 산정하기 위한 수식들을 제시하였다.
본 연구에서는 Neubecker and Randolph (1995)의 토체저항법에 근거하여 사질토와 점성토 각각에 대하여 주묘과정 중 발생하는 지중부 계류체인과 앵커의 상호운동을 동시에 해석할 수 있으며 단일 또는 복합 지반조건에서의 앵커궤적과 최대침투깊이를 계산할 수 있는 수치해석기법을 제시하였다. 앵커는 부위별로 생크 (shank), 스톡 (stock), 풀루크 (fluke) 그리고 계류체인 (mooring chain)으로 구분하고 각 부위를 작은 소구간들로 분할하여 주묘과정 중 각 소구간에서의 지지력과 마찰력을 연속적으로 산정함으로써 단일 토질 조건을 포함하여 점성토와 사질토의 다층 토질조건에서도 적용할 수 있도록 하였다. 앵커에 대해서는 일반적으로 많이 사용하고 있는 스톡리스 앵커 (또는 풀루크 앵커)를 대상으로 하였으며 관련 파라미터들의 보정을 위하여 NCEL (1984)의 실험도표와 그리고 Vryhof (2015)의 Stevin MK3 앵커의 도표를 이용하였다.
2. 단일 지반조건에 대한 주묘해석
2.1 기본방정식의 전개
Fig. 2에서 보이는 바와 같이 선박견인에 의한 앵커침투는 풀루크 하면 방향으로 진행되며 새클에 연결된 지중 계류체인은 역 케티너리 형상을 보이게 된다 (DnV-EP-E301, 2012). 계류체인은 dip-down point에서 지면과 만나며 일반적으로 touch-down point까지 지면과 부착된 상태의 접지장 (ground length)을 이루게 된다. 풀루크가 진행하면서 풀루크 하면이 수평면과 이루는 각도 (β)가 점차 감소하며 종국에는 β=0인 상태의 극한 침투깊이 zult에 도달하게 된다. 본 연구에서는 zult의 수치해석적 예측에 중점을 두었다.

Anchor penetration by ship dragging (DnV-EP-E301, 2012)
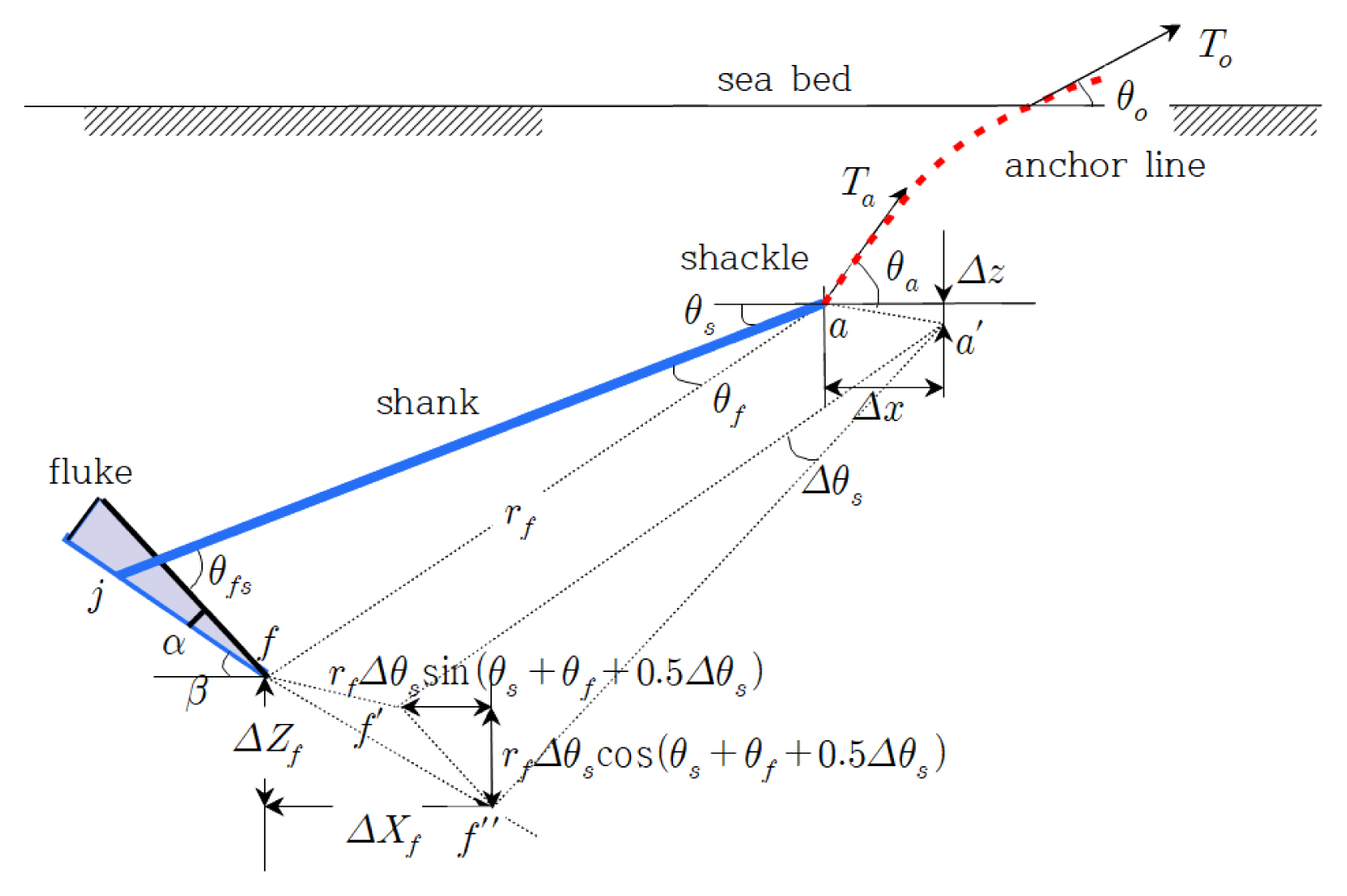
풀루크 앵커의 지중침투 중 발생하는 풀루크 및 생크의 변위를 Fig. 3에 도시하였다. 풀루크가 하면 (지표면과 β의 각을 이룸)을 따라 진행하면서 풀루크 끝점 f가 f′′로 거리 ∆s만큼 이동하면 풀루크 선단의 수평 및 연직변위가 각각 ∆Xf, ∆Yf만큼 발생한다. 이에 따라 생크 역시 침투하게 되며, 새클은 α에서 α′으로 이동하고 수평 및 연직변위가 각각 ∆x, ∆z로 발생하며, 생크가 반시계방향으로 ∆θs 만큼 회전한다.
앵커의 초기위치에서 시작하여 풀루크 끝이 미소거리 ∆s 만큼 축차적으로 진행할 때 임의 계산스텝에서 풀루크 선단 (풀루크 tip) 및 새클의 변위들 간 기학학적 상호관계를 다음과 같이 나타낼 수 있다.
여기서, rf = 새클 - 풀루크 선단 거리, θf = 생크와 선분 (새클-풀루크 선단)의 사이각. θs = 지면-생크 각도이다. 또한 그림에서 rf와 θf는 다음과 같은 기하학적 관계를 이용하여 구할 수 있다.
여기서, Ls = 생크 길이, θfs = 풀루크 각 (생크-풀루크 상면 사이각), lf = 풀루크의 생크 연결점과 생크 선단 사이 (선분 )의 길이이다
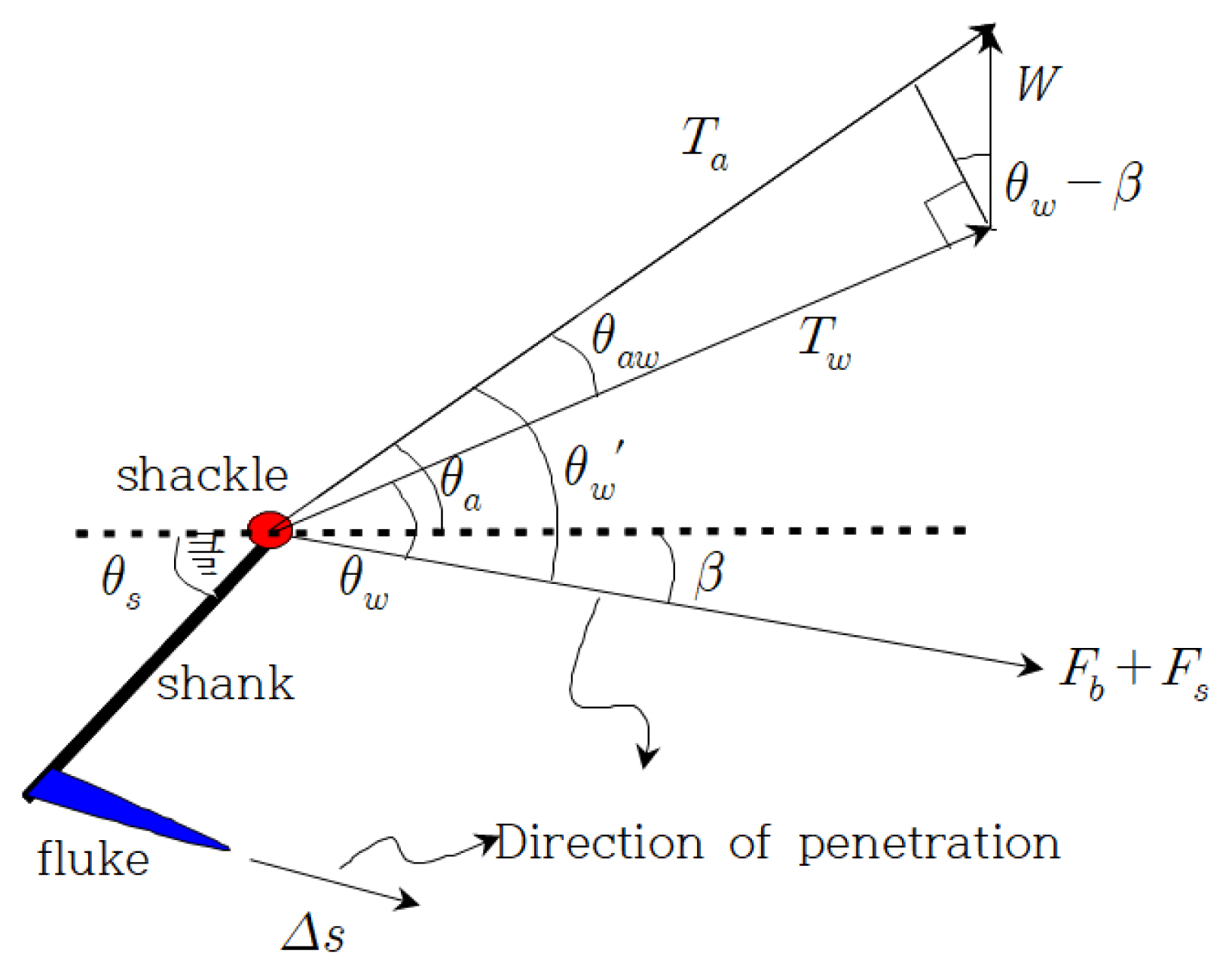
앵커 풀루크가 각도 β로 침투하면서 발생하는 토체 저항력은 새클에 전달되며 지면과 θa의 각을 이루는 계류장력 Ta를 발생시킨다. 앵커의 침투방향과 계류장력의 관계를 Fig. 4에 도시하였다. 그림에서 θw는 계류체인에 전달되는 앵커의 무게 (수중무게) W를 무시했을 때의 가상적 계류장력 Tw의 작용방향과 그리고 풀루크 침투방향간의 사이각도이다. Neubecker and Randolph (1996)는 θw를 앵커와 토질의 특성에 따라 정해지는 고유상수로 정의하였다. 계류장력 Tw는 풀루크와 생크 그리고 스톡 (스톡앵커에 설치)에 작용하는 지지력 (bearing force)의 총합 Fb, 그리고 표면마찰력 (friction force)의 총합 Fs와 힘의 평형을 이루게 된다. 이하 서술의 편이를 위해 β를 침투각 (penetration angle), θs를 생크각 (shank angle), θw를 앵커각 (anchor angle) 그리고 θa를 체인각 (chain angle)으로 각각 호칭하기로 한다.
실제로는 앵커 무게로 인하여 계류장력은 Ta가 되며 지면과 θa의 각을 이룬다. Fig. 4에 대한 기하학적 해석을 통하여 작용력 간의 상호 평형관계를 다음과 같이 나타낼 수 있다.
또한, 침투각 β, 풀루크각 θfs 그리고 생크각 θs은 다음과 같은 관계를 이룬다.
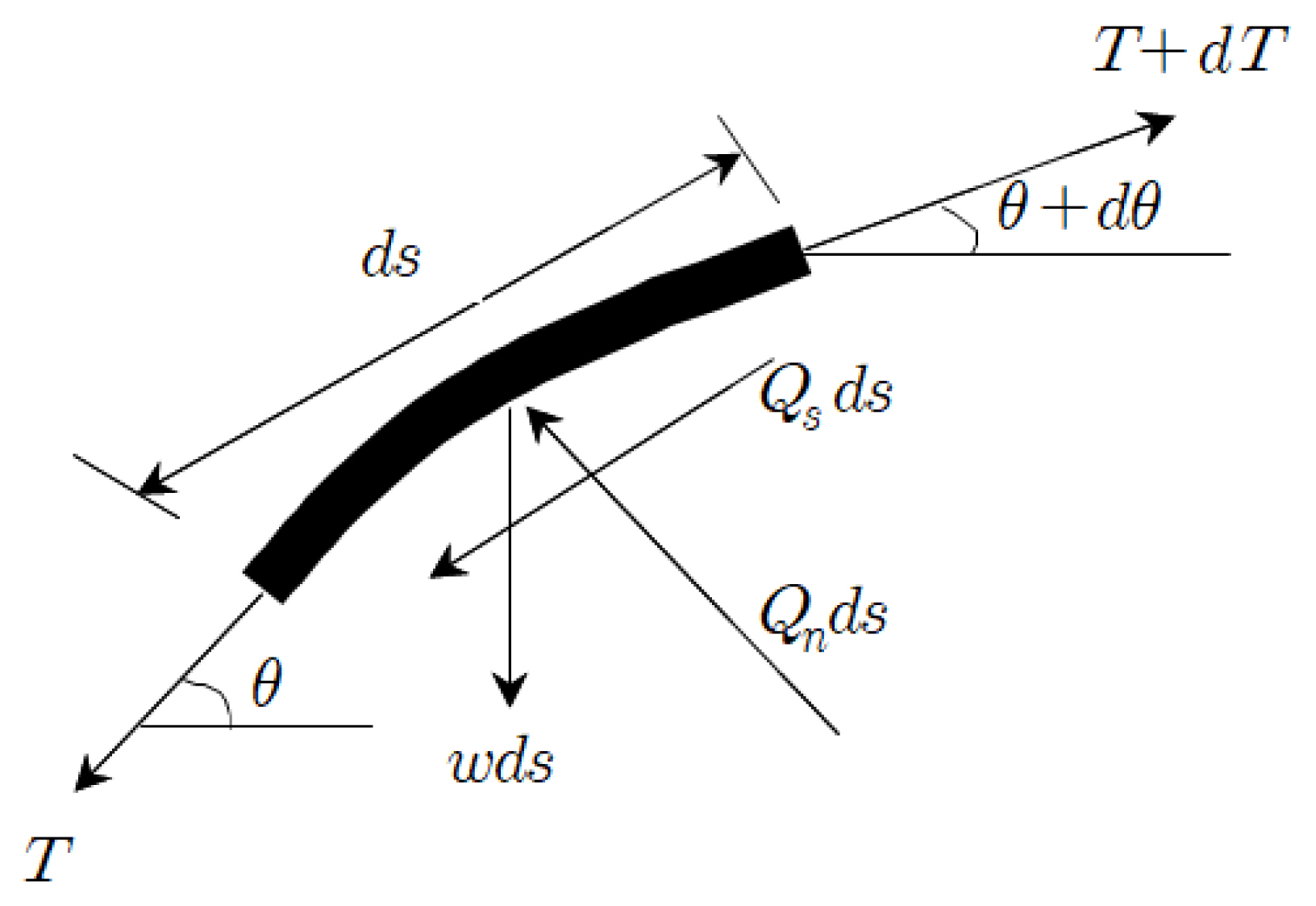
Fig. 3에서 보이는 바와 같이 dip-down 점에서 계류장력 To가 체인각 θo로 작용하면 체인의 지중부는 체인에 작용하는 저항력에 의하여 Fig. 2에서 보이는 바와 같은 역 케티너리 형상을 보이게 된다. 체인 중간의 임의 소구간 ds에 작용하는 힘들은 Fig. 5에서 보이는 바와 같이 장력, 무게 그리고 저항력들로 구성된다. 여기서, T = 장력, w = 단위길이 당 체인의 수중무게, Qn = 단위길이 당 체인에 작용하는 법선저항력 (normal bearing force), Qs = 단위길이 당 체인에 작용하는 접선저항력 (tangential friction force)이다.
Fig. 5에서 임의 점에서의 장력 T와 체인각 θ는 다음과 같은 미분방정식 (Vivatrat et al., 1982; Berteaux, 1976)을 풀어 결정할 수 있다.
한편, Neubecker and Randolph (1995)는 계류체인에 작용하는 법선응력 Qn과 샤클에서의 체인각 θa, 체인장력 Ta의 근사적 관계를 다음과 같이 제시하였다. 본 식은 계류체인의 수중무게를 무시하고 체인각 θ가 매우 작다는 가정하에 유도된 것이다.
2.2 앵커궤적에 대한 수치해석
2.2.1 기본 방정식
수치해석을 위하여 상기 방정식들을 미지수들을 포함하는 형태로 변형하여 정리하면 식 (13) - (20)과 같다.
식 (19)와 식 (20)은 체인 지중부의 해석을 위하여 식 (10)과 식(11)를 총 Nc개의 소구간에 대한 유한차분 형태로 나타낸 것이다. 윗 식들에서 θsp는 한 계산스텝 전의 θs값을 의미한다. 방정식의 개수는 총 2Nc+6개가 되며 총 2Nc+6개의 미지수 (∆x, ∆z, ∆θs, θaw, β, θ1,...,θNc, T1,...,TNc+1)와 폐합을 형성한다. 여기서 체인 상 점 1은 새클에, 그리고 점 Nc+1은 dip-down점과 일치한다. 따라서, (θ1,T1)=(θa,Ta)가 된다. 본 수치해석에서는 dip-down 점에서의 각도와 장력을 별도로 (θo,To)로 정의하며, 체인의 경계조건으로서 각도 θo는 주어지는 것으로 하였다. 통상 체인은 지면에서 접지장을 갖게 되며 θ=0인 경우가 일반적이다. 사실상, 접지장의 형성 여부와 θo의 값은 계류체인의 수중부 해석과 연계하여 결정할 수 있으나 (Wang et al., 2014), 본 수치해석에서는 경계조건으로서 주어지는 값으로 설정하였다.
선박에서 앵커를 투하하고 견인하면 앵커는 풀루크가 완전히 침투할 때까지 다소 불안정한 움직임을 보이게 된다. 이와 같은 앵커의 초기운동은 본 수치해석의 범주를 벗어나기 때문에 본 수치해석에서는 초기조건으로서 풀루크가 지중에 침투되어 있고 생크가 지면에 수평으로 누워있는 경우로 설정하였다. 이 때 Fig. 3에서 침투각 β의 초기조건은 βp=θfs-α가 된다. 수치해석은 β 방향으로의 미소 이동치 ∆s만큼 전진시켜가는 반복계산을 통하여 다음과 같이 수행할 수 있다.
- 초기 값을 이용하여 식 (18)과 식 (15)를 풀어 Ta를 구한다.
- 식 (19)와 식 (20)을 이용하여 dip-down 점에서의 경계조건 θo와 합치될 때까지 θa의 값을 조정한다.
- θa를 식 (17)과 식 (16)에 대입하여 ∆θs와 다음 계산스텝에 사용할 β를 구한다.
- 식 (13), 식 (14)를 이용하여 ∆x와 ∆z를 구한다.
- ∆x, ∆z, ∆θs를 이용하여 새클의 새 좌표 (x,z)를 다음과 같이 갱신한다. 하첨자 p는 한 계산단계 이전을 의미한다. 즉,
- β=0에 근접할 때까지 상기 과정을 반복한다.
그리고 각 계산단계 별 풀루크 선단 (tip)의 좌표는 다음과 같이 구할 수 있다.
초기조건은 위에서 언급하였던 것처럼 생크가 지면에 누운 상태로서 x=z=θs=0로 하였다. 초기 상태에서의 풀루크 끝의 좌표 (Xf,Zf)는 앵커의 기하학적 형상을 고려하여 쉽게 계산할 수 있다.
본 연구에서는 비교목적 상 식 (19), (20) 대신에 Neubecker and Randolph (1995)의 근사식 (12)를 변형한 다음과 같은 식을 사용하여 별도로 계산을 수행하였다.
2.2.2 지지력과 마찰력의 결정
Fig. 4에서 앵커에 작용하는 저항력은 면에 직각으로 작용하는 지지력 (bearing force) Fb와 측면에 평행하게 작용하는 마찰력 (friction force) Fs로 구성되며 이들은 생크와 풀루크 각각의 저항력을 합산하여 구한다. 앵커침투가 진행되면서 각 부위의 위치가 변하게 되며 따라서 이들 저항력도 변하게 된다. 따라서, 상기 수치해석의 반복계산에서 각 계산스텝마다 앵커 저항력을 갱신해주어야 한다. 이 작업은 생크, 스톡, 풀루크 그리고 계류체인 (지중부) 각각을 수 개의 길이방향 소구간으로 분할하고 계산과정 중 각 소구간의 중심점 위치를 연속적으로 추적하여 그 중심점에서의 토압을 계산하여 입력하는 방식으로 수행하였다. 침투과정 중 앵커의 형상은 불변임으로 각 계산스텝마다 새클의 위치 (x,z) 및 생크각 θs가 결정되면 상기 부위 별 소구간 중심점의 좌표를 쉽게 구할 수 있다. 물론, 각 소구간에서의 저항력 작용면적, 즉, 지지력 면적 Ab와 마찰면적 As는 각 소구간의 형상을 고려하여 미리 결정해 놓으면 된다.
여기서는 앞서 기술한 대로 말뚝과의 유사성을 고려하여 앵커의 저항력을 결정하였다. 앵커가 전체적으로 풀루크 하면 방향으로 전진하기 때문에 풀루크의 저항력은 연직말뚝의 축방향 지지력 및 마찰력과 유사하게 결정할 수 있다. 그러나 풀루크와 각을 이루는 생크의 거동은 연직파일 보다는 경사파일의 경우에 더 가깝다. 경사진 생크가 풀루크 방향으로 이동할 때 임의 소구간 ∆l에 작용하는 저항력 f는 Fig. 6에서 보이는 바와 같이 일단 직각방향의 저항력 fn을 구한 다음 이의 풀루크 진행방향의 성분으로 구하였다. 스톡이 부착되어 있는 경우, 스톡은 일반적으로 풀루크 진행방향과 직각을 이루므로 풀루크의 경우와 동일한 방식으로 저항력을 산정해주면 된다.
앵커 각 부위의 소구간에 작용하는 지지력 f는 지지력 fb와 마찰력 fs로 구성되며 앵커 전체에 작용하는 총 저항력 FT를 다음과 같이 구한다.
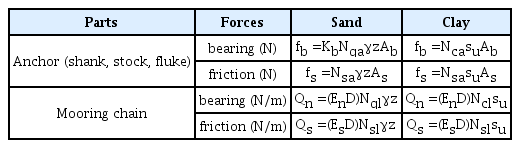
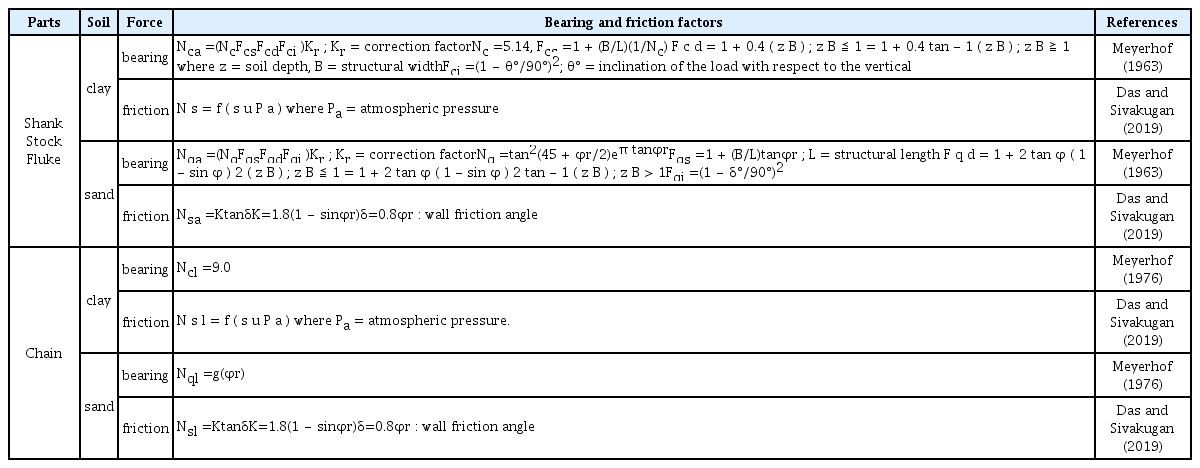
반복계산을 수행하면서 계류체인도 위치가 바뀌게 되며 체인에 작용하는 단위 길이 당 지지력 Qn과 마찰력 Qs도 각 스텝마다 갱신해주어야 한다. 이와 같이, 앵커와 체인의 각 미소 구간에 작용하는 저항력 및 단위 길이당 체인에 작용하는 힘들을 Table 1의 식들을 이용하여 산정하였다. 사질토 지지력에서 Kb는 횡수동토압계수이며 일반적으로 0.5의 값을 갖는다 (Miedema et al., 2007). 표에서 Nqa, Nγa, Nca는 각각 상재하중, 모래단위중량, 점성에 대한 지지력계수이며, Nsa는 마찰력 계수를 의미한다. 그리고 Nql과 Nsl은 각각 계류체인의 지지력 계수와 마찰계수이다. 여기서, γ는 모래의 수중단위중량을, su는 점토의 비배수전단강도를 의미한다. En과 Es는 유효체인직경을 구하기 위하여 체인직경 D에 곱해지는 승수이다 (Degenkamp and Dutta, 1989). 본 연구에서는 DnV-RP-E301 (2012)의 En=2.5, ES=11.3를 사용하였다.
2.2.3 최대침투깊이의 직접 결정
앵커 침투가 진행되면서 풀루크 하면 각 β가 영에 근접하며 풀루크가 수평으로 이동하게 된다. 이 경우 계류체인도 일정한 형상을 유지하며 새클에서의 장력 Ta와 체인각 θa도 일정한 값에 도달하게 된다. 이때 dip-down 점에서의 장력을 극한파주력 (ultimate holding capacity)이라 칭한다. 최대침투깊이 및 극한파주력은 식 (13) - (18)에 β=0을 대입하여 정리한 다음과 같은 연립방정식들을 풀어 결정할 수 있다.
여기에서도 식 (28) - (29) 대신에 계류체인의 수중 무게와 체인 각도가 공히 작다는 가정하에 Neubecker and Randolph (1995)가 제시한 근사식인 식 (23)을 이용할 수도 있다. 본 연구에서는 상기 연립방정식을 풀기 위하여 이분법 (bisectional method)을 적용하였으며, 주어진 θo를 만족시키는 새클의 침투깊이를 먼저 구한 후, 이로부터 앵커의 기하학적 형상을 고려하여 풀루크 선단에서의 최대침투깊이를 결정하였다.
3. 수치해석의 보정 및 검증
3.1 수치해석의 보정
앵커에 대한 수치해석 문헌들을 보면, 앵커와 계류체인의 저항력을 산정하기 위한 식들은 거의 동일하나 산정식에 포함된 저항력 계수 (지지력 및 마찰계수)들에서 차이가 남을 알 수 있다. DnV-RP-E301 (2012)은 과거 실해역 관측결과에 근거하여 점성토에 대한 앵커와 계류체인의 계수 값들을 제시하였다. 또한, Liu et al. (2010)은 점성토와 사질토 각각에 대하여 이들 계수 값들에 대한 포괄적인 평가의견을 제시한 바 있다. 그러나, DnV-RP-E301 (2012, p. 23)도 지적하였듯이 현재로서는 이들 수치해석이 대부분 점성토에 치중되어 있으며 사질토를 대상으로 한 문헌은 매우 희소한 편이다. 따라서, 본 연구에서는 전 Fig. 7. StevinⓇ MK3 (adapted from Vryhof, 2015) 절에서 수립한 수치해석기법을 이용하여 먼저 사질토의 적정 저항력 계수 값의 범위를 정하기 위한 수치실험을 수행하기로 한다. 그리고, 본 사질토에서의 방법론을 참조하여 점성토에 대한 수치해석의 성능을 검토하기로 한다. 본 수치실험에서 Fig. 7과 같은 Vryhof (2015)의 StevinⓇ MK3 앵커의 자료를 이용하기로 한다. 본 앵커는 매뉴얼에 1 톤에서 50 톤에 이르기까지 앵커 중량별 그리고 토질별 최대 침투깊이 및 침투거리 그리고 극한파주력의 관계를 독취할 수 있는 도표들이 잘 제시되어 있다.
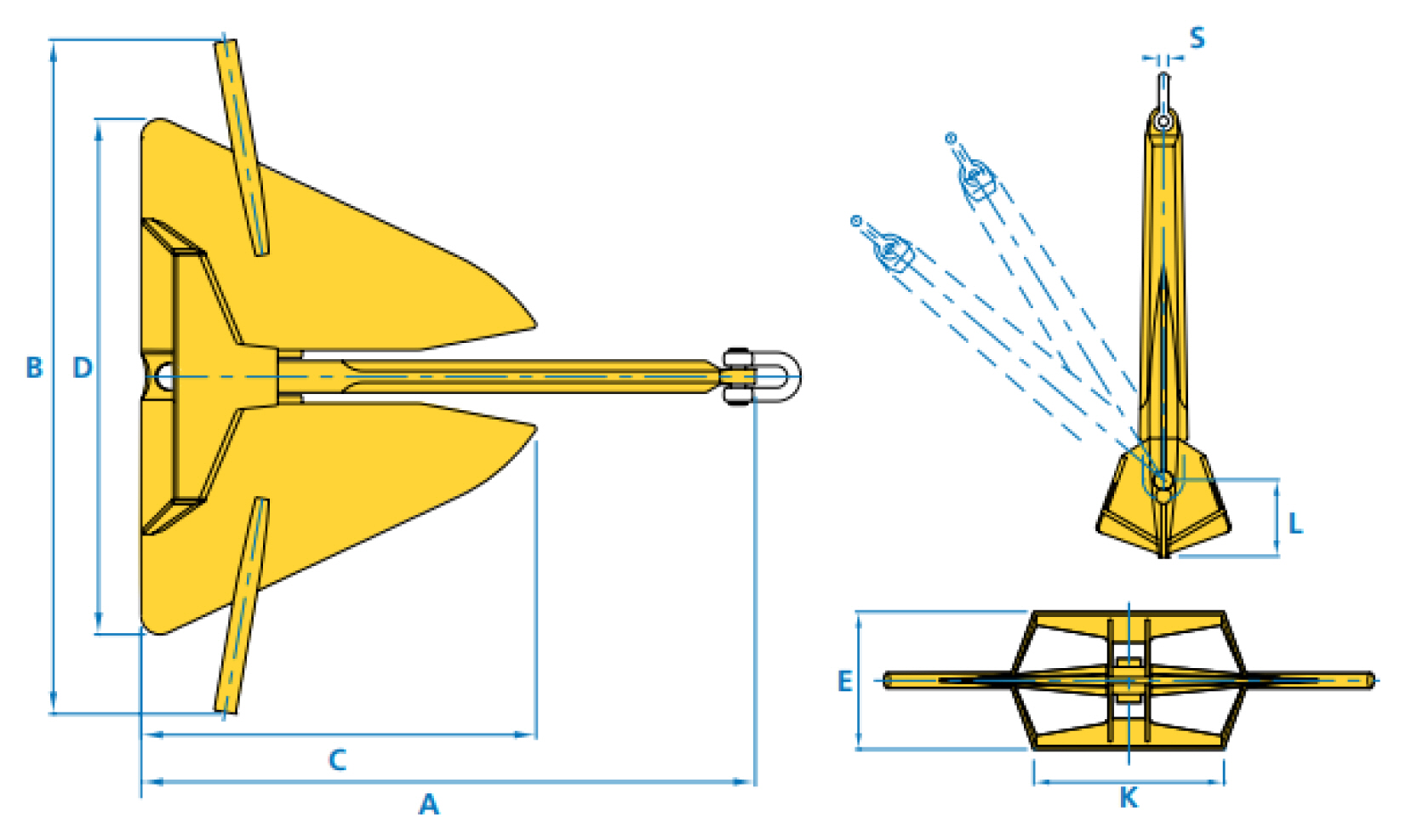
Stevin® MK3 (adapted from Vryhof, 2015)
풀루크에 부착되어 있는 스톡을 포함하여 Fig. 7에 제시되어 있지 않은 부위들의 기하학적 제원은 Fig .7의 제원과 그리고 타 자료들에서의 실물사진을 비교하여 근사적으로 정하였다. 풀루크 앵글 (풀루크 상면과 생크사이의 각도)은 매뉴얼에 명시된 대로 점성토와 사질토 공히 θfs=32º로 정하였다. 계류체인의 직경과 중량은 앵커의 질량에 따라 정해지며 Korean Register (2021)의 자료를 참조하여 정하였다. 수치해석의 전처리 작업으로서 생크와 풀루크 및 계류체인을 각각 100개씩의 소구간으로 분할하여 각 소구간의 bearing 면적과 마찰면적을 미리 산정하였다.
본 수치해석의 예비실험 결과, 앵커의 침투깊이 및 파주력은 앵커각 ( θw)가 증가할수록, 그리고 dip-down점의 체인각 (θo)이 영에 근접할수록, 그리고 앵커의 지지력계수 Nqa가 증가할수록 증가하는 것으로 나타났다. 반면, 앵커체인의 경우는 반대성향을 보이며, 체인의 지지력계수 Nql가 감소할수록 침투깊이와 파주력은 증가하였다. 이와 같은 성향을 염두에 두고 실험조건을 Table 1의 앵커 지지력계수 Nqa를 5와 25의 두 가지로, 그리고 체인 지지력 계수 Nql은 50, 100, 150, 200과 250의 다섯 가지로 변화시켜 가며 수치실험을 수행하였다. 일반적으로 사질토에서의 마찰력은 지지력보다 작다고 판단되어 마찰력 계수에 대해서는 별도의 변화를 시도하지 않았으며 Das and Sivakugan (2019)의 식으로 산정한 마찰력 계수를 일관되게 사용하였다. 수치실험은 마찰각이 37.5º이며 포화단위중량이 18.5 kN/m3 인 중간조밀한 모래 (medium sand)를 대상으로 하였다. 앵커각 θw는 1.0θfs로, 그리고 체인각은 θo=0으로 설정하고 식 (25) - (29)를 이용하여 최대침투깊이 및 극한파주력을 직접 계산하였다. 여기서 극한파주력은 지중부 계류체인의 dip-down점에서의 장력 To을 의미한다.
상기 조건 하에서 수치해석을 수행하고 계산된 최대침투깊이를 Fig. 8에, 그리고 극한파주력을 Fig. 9에 각각 도시하였다. 각 그림들에서는 Nqa=5와 여러 Nql의 조합에 의한 결과는 파란색으로, 그리고 Nqa=25와 여러 Nql의 조합에 따른 결과는 붉은색으로 표시하였다. Fig. 8을 보면 Nqa가 증가할수록, 그리고 Nql이 감소할수록 최대 침투깊이가 증가함을 알 수 있다. Nqa=5에서는 Nql=50-100에서, 그리고 Nqa=25 에서는 Nql=100-150에서 계산결과가 Vryhof의 값과 유사하게 나타나 있으나 전반적으로 Nqa=25에서 합치정도가 나음을 볼 수 있다. 극한파주력을 도시한 Fig. 9를 보면 이 역시 상기 침투깊이와 마찬가지로 Nqa가 증가할수록, 그리고 Nql이 감소할수록 극한파주력이 증가한다. 그러나 여기에서도 Nqa=5보다는 Nqa=25의 경우가 도표 값에 더 유사함을 볼 수 있다.

Comparison of maximum penetration depth calculation results and Vryhof (2015) chart values according to changes in bearing capacity coefficient of anchor (Stevin® MK3) and chain (medium sand)
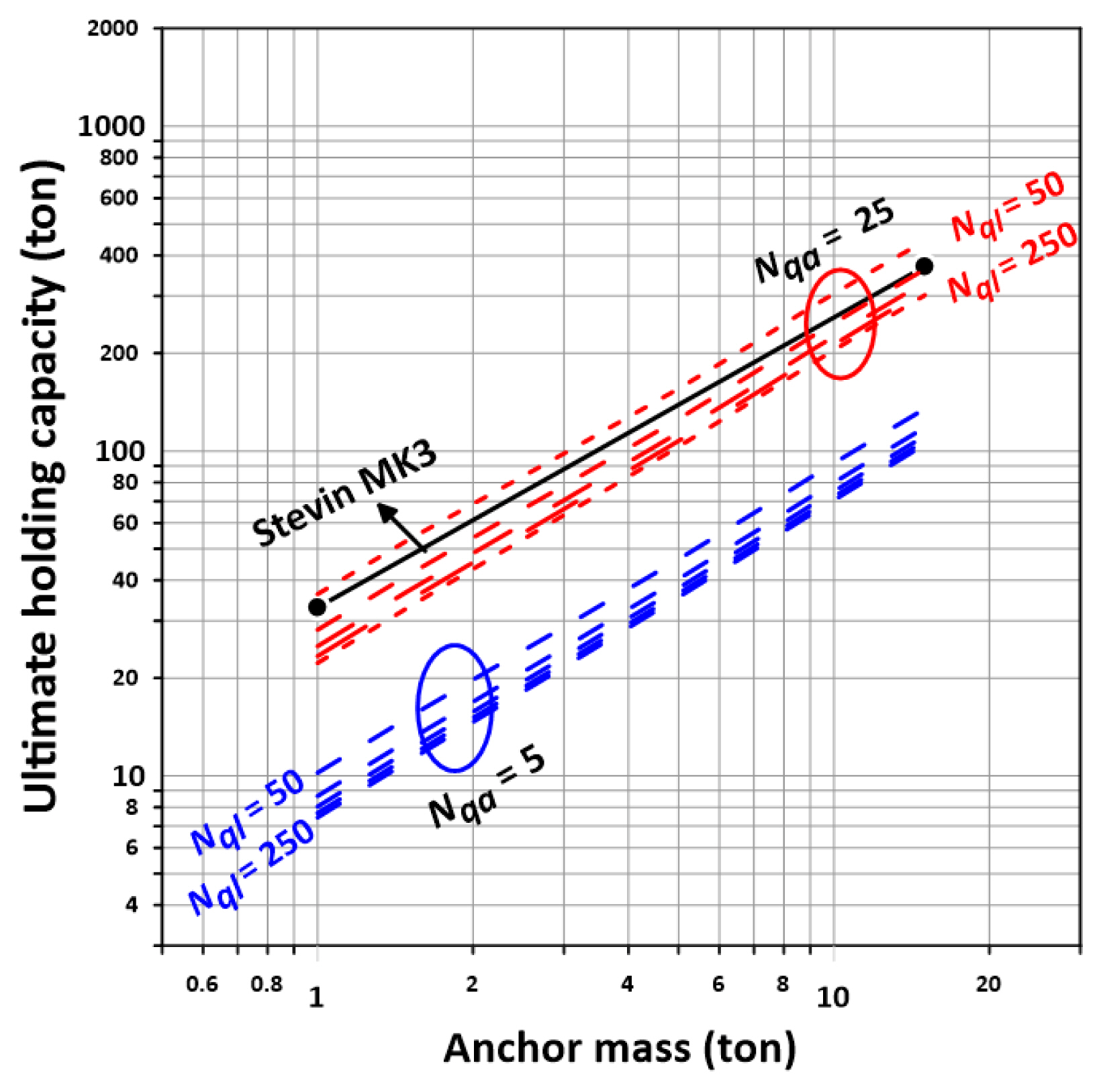
Comparison of ultimate holding capacity calculation results and Vryhof (2015) chart values according to changes in bearing capacity of anchor (Stevin® MK3) and chain (medium sand)
상기 수치실험은 토층 내 지지력 계수가 일정하다는 가정하에 수행된 것으로서 실제 심도에 따라 토압이 변하는 사질토층의 양상을 정확히 재현한다고 보기는 어렵다. 그러나, 본 수치실험을 통하여 전반적으로 앵커의 지지력계수는 약 25 이하에서 그리고 체인의 지지력 계수는 약 100 이상에서 형성되는 것으로 추측해 볼 수 있다. 최소한 앵커와 체인이 동일한 지지력 계수를 공유하는 것은 불합리할 것으로 판단되었다. 본 실험에서 앵커 지지력계수가 체인보다 낮게 나타난 것은 다소 예상 밖이나 Rowe and Davis (1928)와 ASCE (1984) 역시 매설 파이프의 수평운동의 극한지지력에서 약 20 이하의 지지력계수가 발생할 수 있음을 보인 바 있다.
상기와 같은 대략적인 이해를 전제로 기존의 여러 지지력과 마찰력 산정식들을 적용하여 수치해석을 수행하였다. 그 결과, 앵커 (풀루크, 생크, 스톡)에 대해서는 Meyerhof (1963)가 제안한 연속보 기초의 지지력 식을, 그리고 체인에 대해서는 Meyerhof (1976)의 연직파일의 지지력 식을 사용하는 것이 상기 판단을 비교적 잘 충족시키는 것으로 나타났다. 체인이 단일말뚝의 성향을 보이며 지지력계수가 크게 나타나는 것은 체인의 유연성으로 인하여 강체 연속보에 비하여 각 소구간이 독립적으로 작용하는 성향이 더 두드러지게 나타나기 때문인 것으로 판단된다. 이 두 식의 주요 저항력 계수를 후술할 점성토 지지력 계수와 함께 Table 2에 제시하였다. 표에서 Nqa와 Nca의 산정식에는 일종의 보정계수 (correction factor) Kr이 포함되어 있으며 이는 지지력 계수의 세부조정을 위한 것이다. 보정계수는 이와 같이 앵커의 지지력계수에만 적용하였으며 마찰력과 그리고 체인에 대해서는 별도의 보정없이 본래의 산정식을 그대로 사용하였다.
3.2 수치해석의 검증
3.2.1 사질토
상기 strip 기초와 연직파일의 지지력 계수를 이용하여 식 (13) - (20)을 풀어 앵커의 침투궤적 및 극한파주력을 구하기 위한 수치해석을 수행하였다. 적용 토체는 상기 보정절차에 사용하였던 중간조밀한 모래 (medium sand)를 대상으로 하였으며, 계산조건은 앵커각을 θw=1.0θfs으로, 그리고 dip-down점의 체인각을 일반적인 접지장을 갖는 경우의 θo=0o로 설정하였다.
극한파주력 그리고 최대침투거리를 계산하여 그 결과를 Vryhof (2015)의 도표값들과 함께 Fig. 10에 도시하였다. 단, 여기서 최대침투깊이는 앵커의 궤적에서 β=0.01o에서의 침투깊이로 설정하였으며, 비교치는 Vryhof 도표값 대신 NCEL (1984)의 지침을 참조하여 1 플루크 길이를 도시하였다. 계산치와 도표 값들을 비교해보면 전반적으로 변화양상은 유사하나 계산치들이 다소 작음을 알 수 있다. 앞서 기술하였듯이 지지력 계수가 감소하면 침투깊이와 UHC는 감소한다. 지지력 계수에 보정계수 Kr=0.5을 적용한 Fig. 11을 보면 세 가지 항목 모두의 일치 정도가 많이 개선되었음을 알 수 있다. 추후 사질토 해석에서는 을 사용하기로 한다.
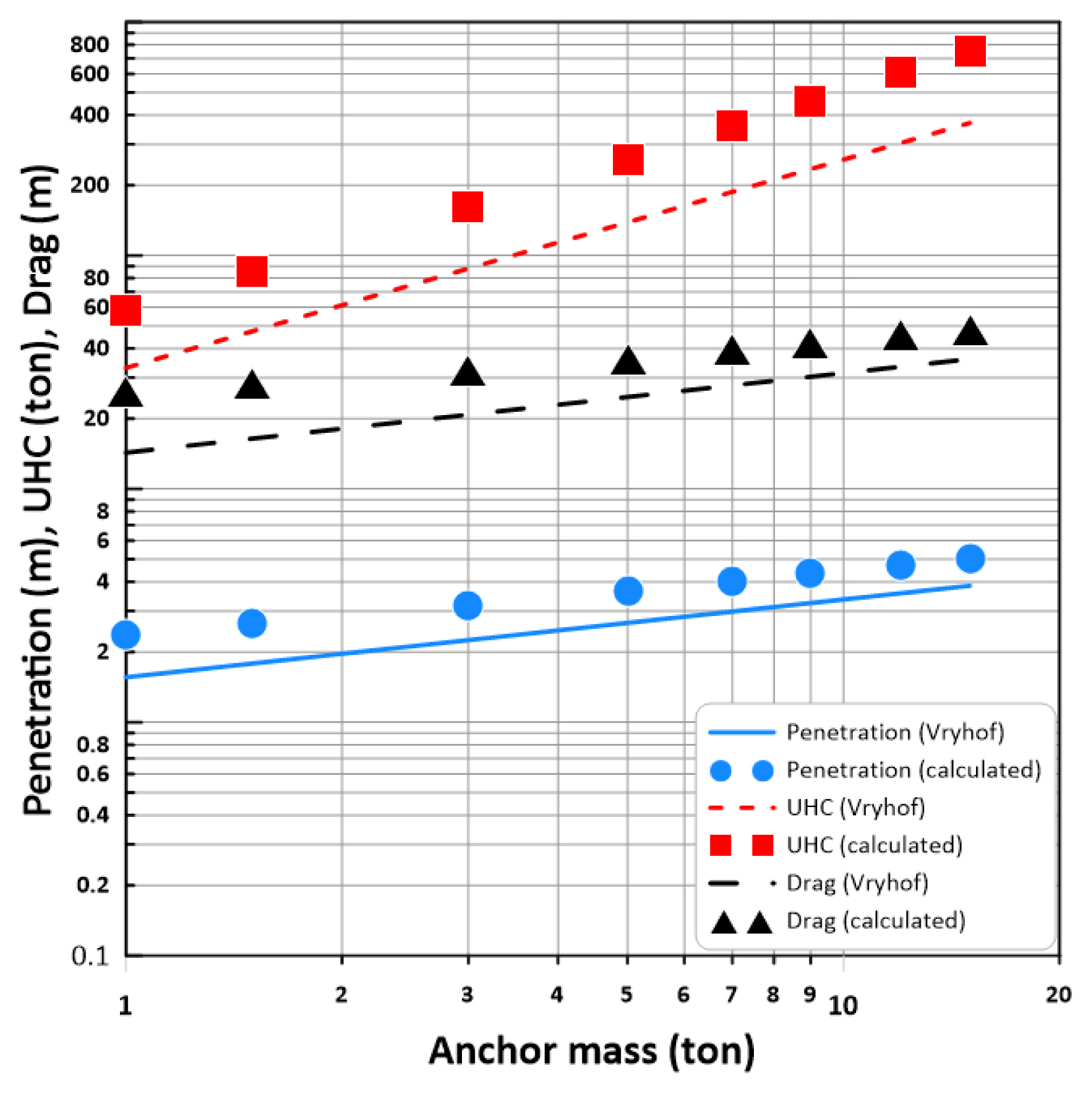
Comparison of calculation results using the force coefficients derived through numerical experiments and chart values of Vryhof (2019) (medium sand) : correction factor Kr =1.0
3.2.2 점성토
점성토에 대한 수치실험은 사질토 조건과 마찬가지로 앵커는 연속보 기초의 식을 그리고 계류체인은 연직파일의 식을 이용하여 수행하였다 (Table 2). 토질조건은 비배수전단강도가 37.5 kPa, 포화단위중량이 18.45 kN/m3 인 중간단단한 점토 (medium clay)를 사용하였다. 점성토 조건에 대한 앵커의 저항력 계수는 많은 연구자들에 의하여 제시되어 왔다 (Liu et al., 2010). 또한, DnV-RP-E301 (2012)는 자체 개발한 수치해석의 저항력 계수들을 현장관측 데이터를 이용한 후추산 (back-analysis)을 통하여 도출하였으며 그 결과를 Table 3과 같이 제시하였다. 본 점성토 수치실험에서는 Table 2의 점성토 저항력 계수와 그리고 본 DnV의 저항력 계수를 각각 사용한 수치해석 결과들을 비교하기로 한다.

Resistance force coefficients of anchor and mooring chain (DnV-RP-E301, 2012)
Table 3에서 αf는 부착력 계수 (adhesion factor)로서 점성토의 예민비 (sensitivity ratio) St의 역수로 나타내진다. 콘관입시험 (CPT)을 이용하여 St를 간접적으로 구할 수 있으며 (Abuhajar et al., 2010; Begemann, 1965), 이로부터 구한 점토의 αf의 값은 약 0.3-0.9의 값을 갖는다. 여기에서는 Murff et al. (2005)이 제안한 αf=0.4를 사용하였다.
저항력 계수에 대하여 Table 2의 식들을 사용한 경우 (Kr=1.0)와 상기 DnV의 값을 사용한 경우에 대한 수치해석결과를 각각 Fig. 12와 Fig. 13에 도시하였다. 사실상, 사용된 DnV 계수값들은 또 다른 수치해석의 후추산 (back-analysis) 과정을 통해 나온 값들이나 본 수치해석의 계수값들과 거의 유사한 결과를 주는 것으로 나타났다. 그러나, 두 방법 공히 최대침투깊이는 도표값과 양호한 일치를 보이나 극한파주력에서 다소 큰 차이를 보이고 있다. 이에 대해서는 추후 실증실험 결과를 이용한 수치해석의 검증에서 재검토할 계획이다.

Comparison of calculation results using the force coefficient derived through numerical experiments and chart values of Vryhof (2015) (medium clay)
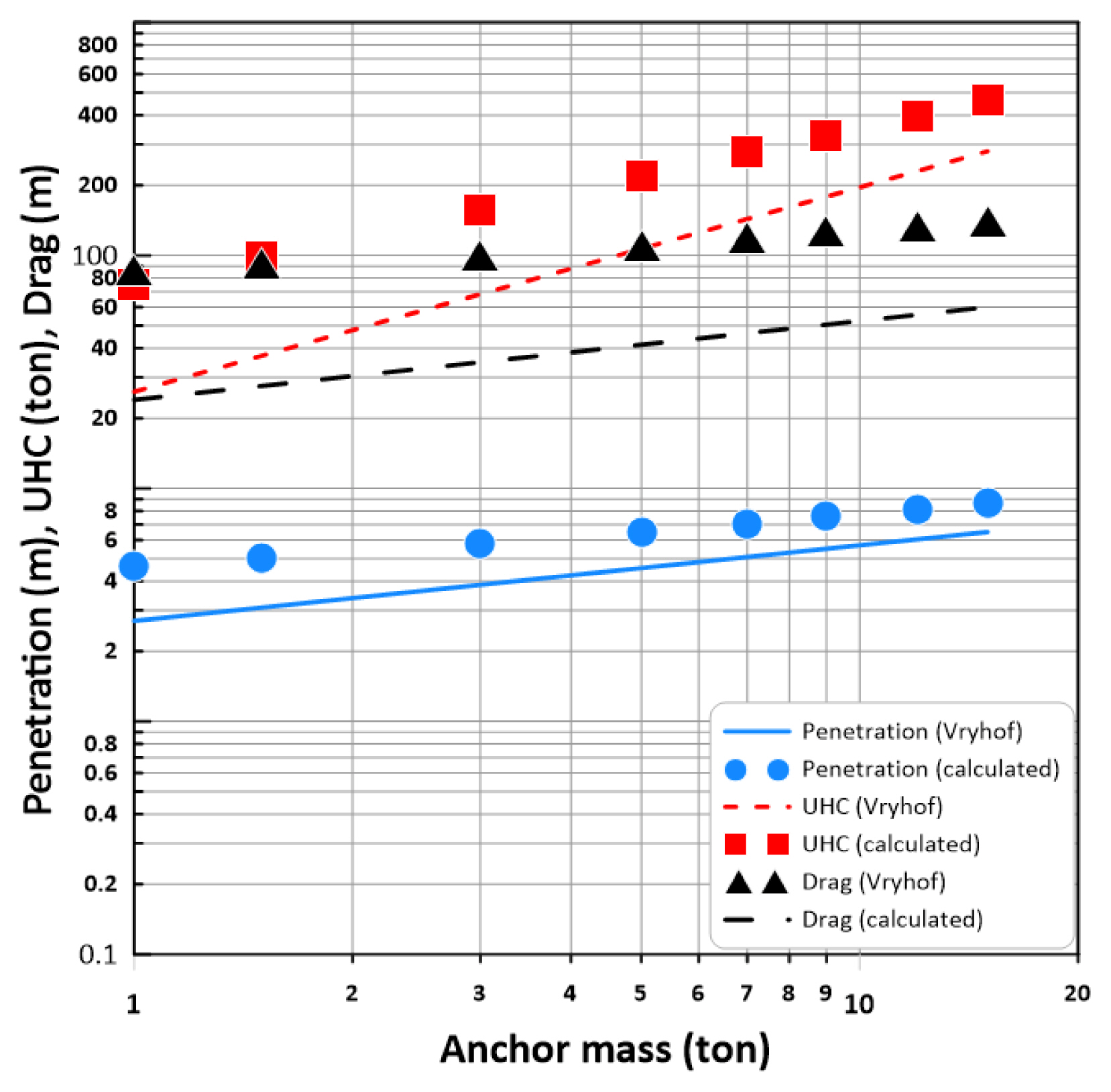
Comparison of calculation results using the force coefficient of DnV-RP-E301 (2012) and chart values of Vryhof (2015) (medium clay)
전술한 모래의 경우와 마찬가지로 보정계수 Kr=0.2를 사용하여 지지력 계수를 감소시켜 계산한 결과를 Fig. 14에 도시하였다. 극한파주력을 포함하여 전반적으로 계산결과가 도표결과에 많이 근접했음을 볼 수 있다. 추후 점토해석에서 보정계수 Kr=0.2를 사용하기로 한다.
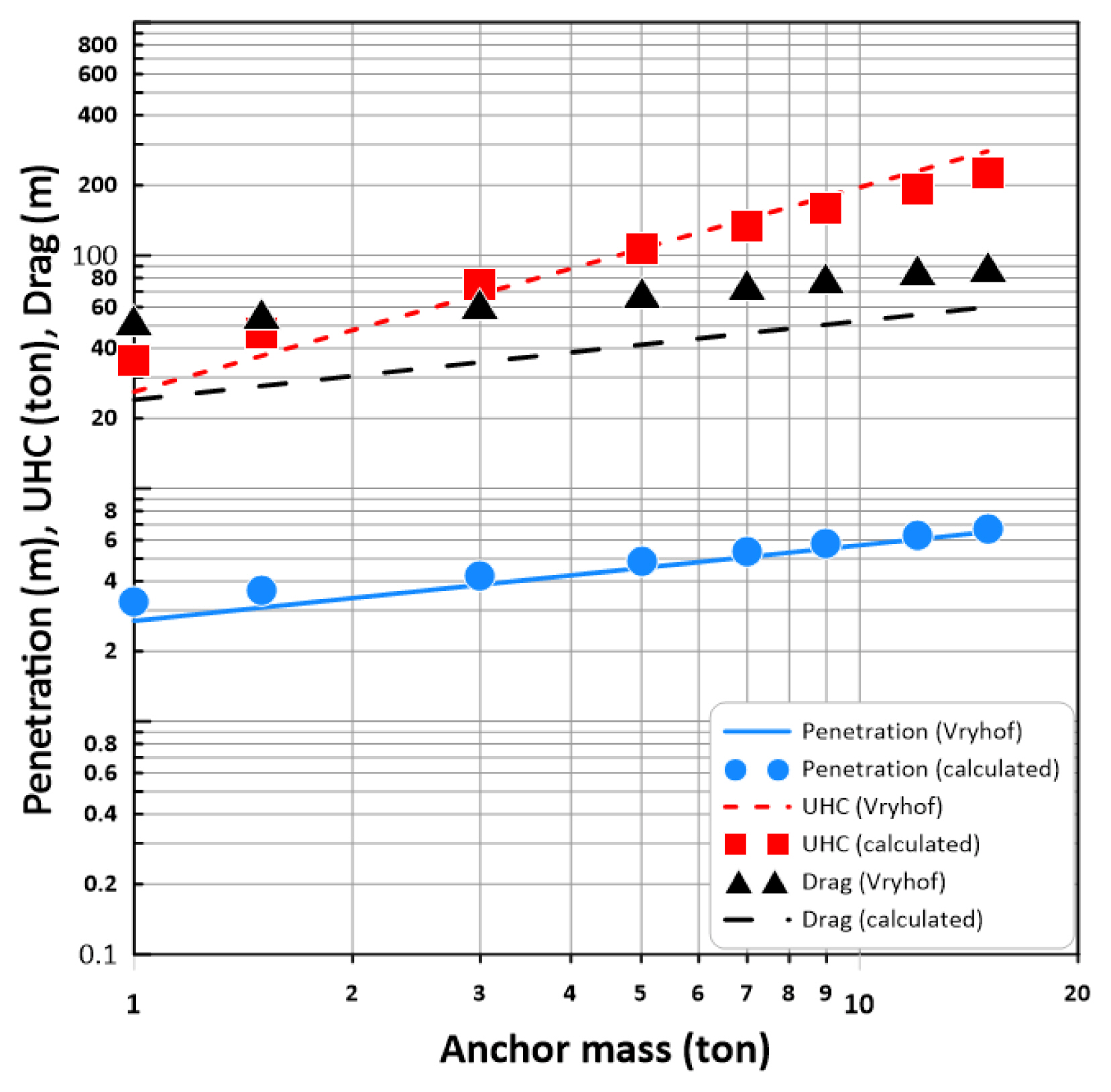
Comparison of calculation results using the force coefficient derived through numerical experiments and chart values of Vryhof (2015) (medium clay) : correction factor Kr = 0.2
Fig. 15와 Fig. 16은 각각 위에서 사용한 중간조밀한 모래 (medium sand)와 중간단단한 점토 medium clay)에 대하여 Table 2의 저항력 계수들을 이용하여 앵커 및 체인의 궤적을 계산한 결과이다. 사용된 앵커질량은 2.1 톤으로 하였다. 두 그림에서 앵커와 계류체인의 궤적과 그리고 계류체인의 역 캐티너리 형상이 잘 재현되어 있음을 볼 수 있다. 모래는 점토에 비하여 최대침투깊이가 형성됨을 볼 수 있다. 그림들에는 식 (25) - (29)로 직접 계산한 최대침투깊이도 같이 도시되어 있다. 이 역시 수치해석의 종국적인 궤적과 잘 일치하는 것으로 나타났다.

Calculation results of anchor trajectory and maximum penetration depth (UED) for medium sand: Stevin MK3 anchor 2.1 tons

Calculation results of anchor trajectory and maximum penetration depth (UED) for medium clay: Stevin MK3 Anchor 2.1 tons
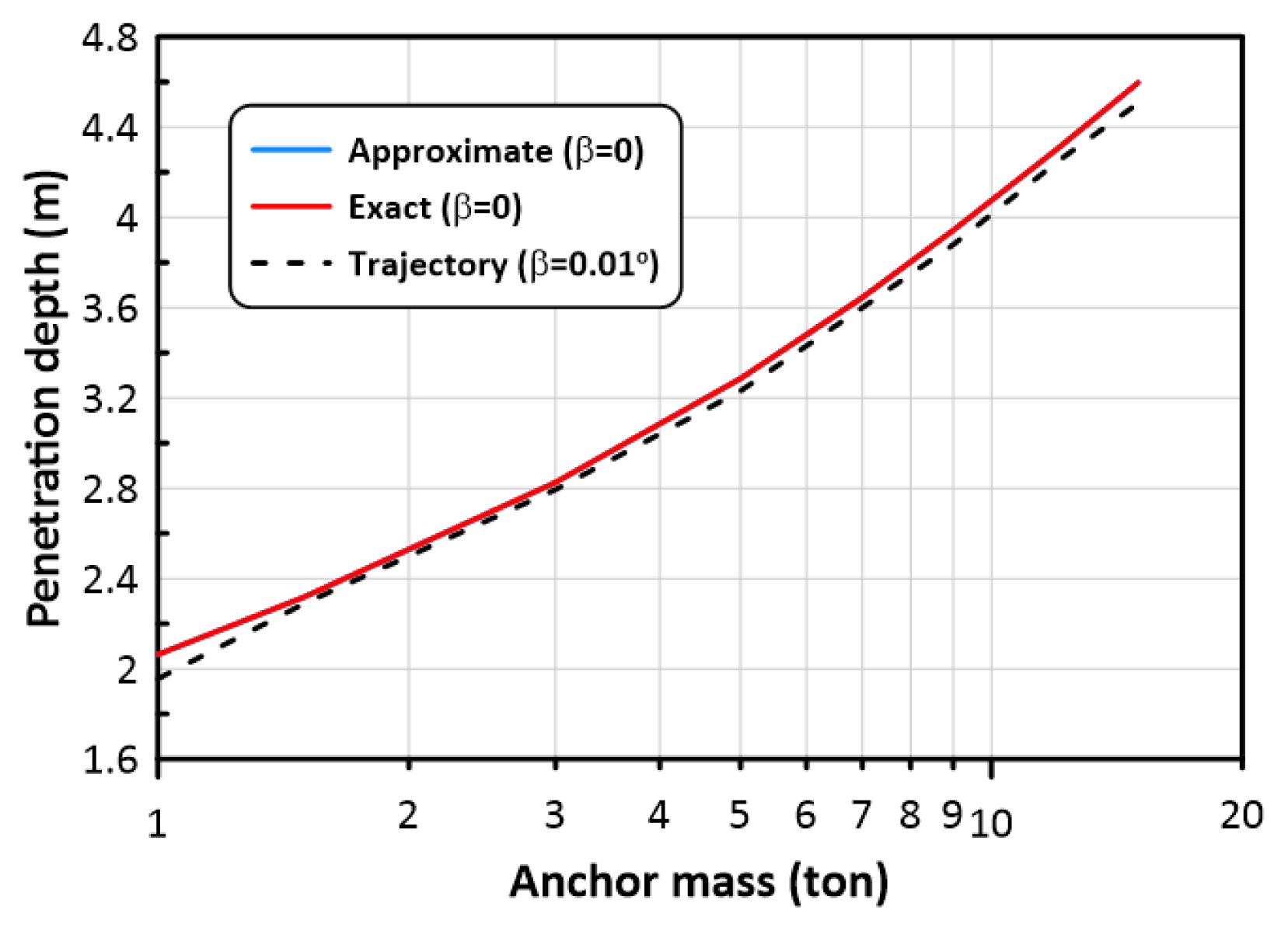
마지막으로 최대침투깊이 (풀루크 선단 기준) zued에 대한 다음의 세가지 산정방법의 결과에 대하여 검토하였다.
- 방법 1: 근사식 (23)을 이용하여 β=0에 대한 zued를 바로 구하는 근사해(Approximate)
- 방법 2: 식 (25) - (29)를 해석하여 β=0에 대한 zued를 바로 구하는 정확해(Exact)
- 방법 3: 식 (13) - (20)을 해석하여 앵커의 침투궤적을 계산하고 β=0.01o에 해당하는 침투깊이를 산정하는 방법 (Trajectory)
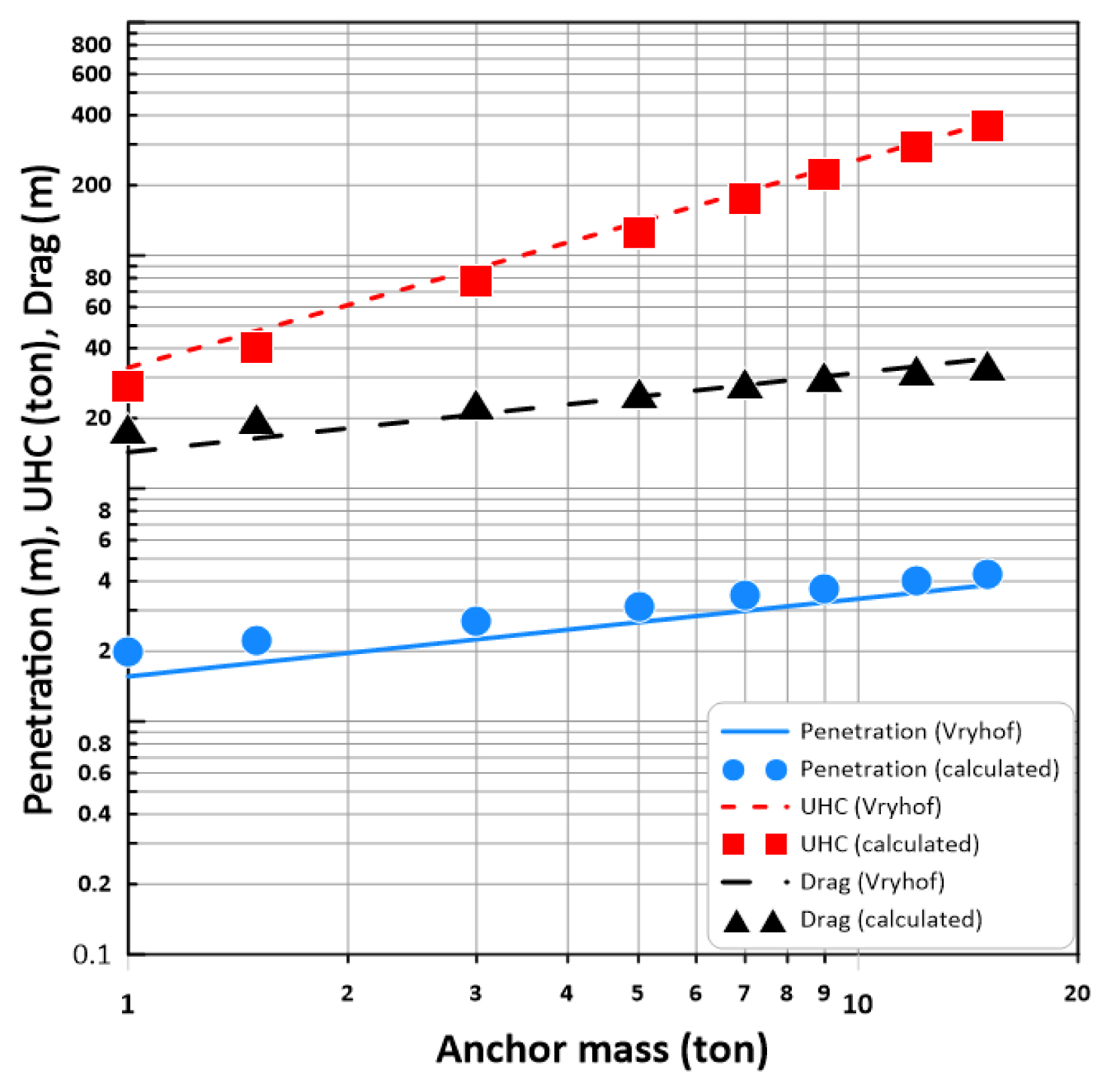
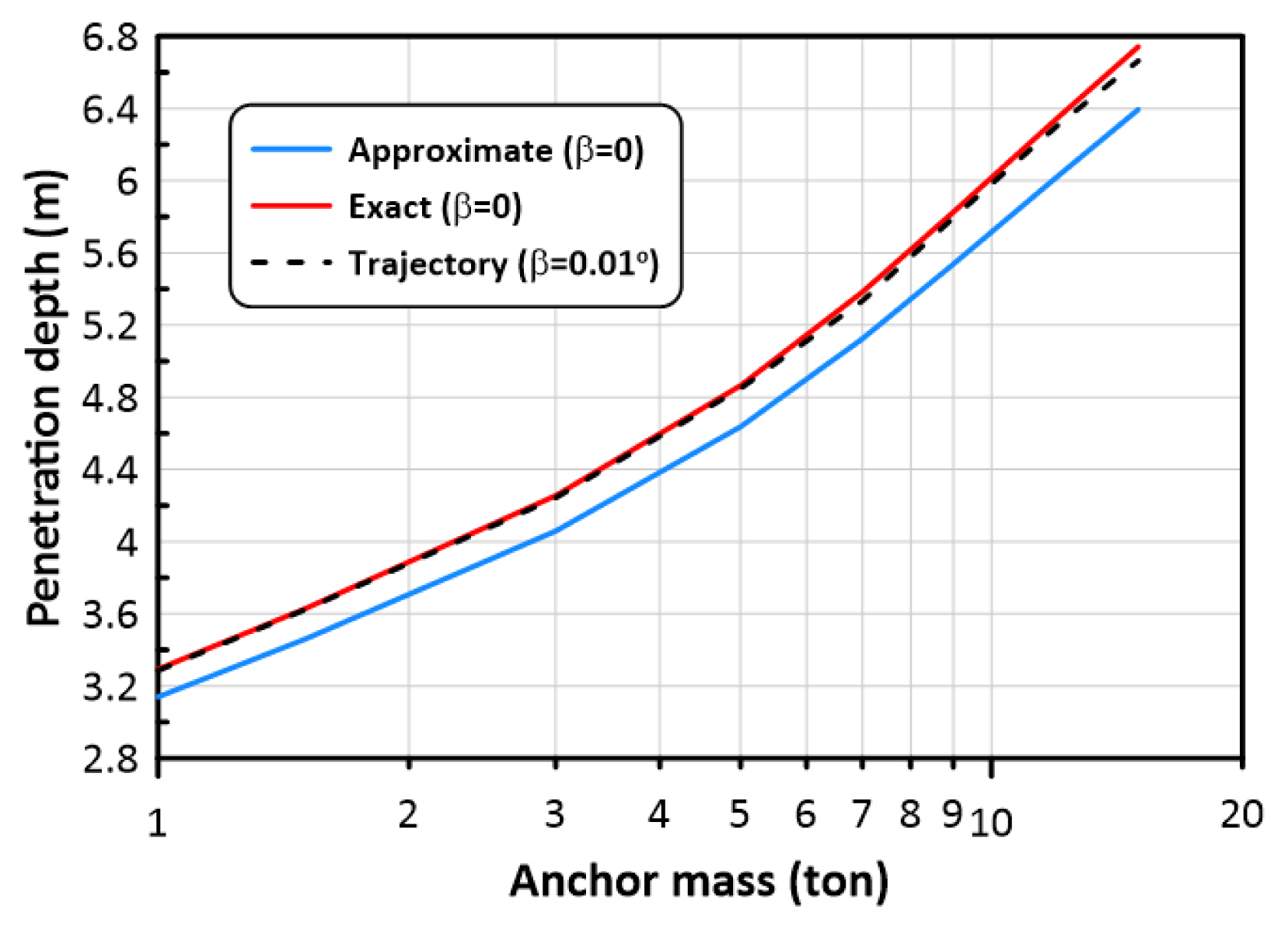
Fig. 17과 Fig. 18은 각각 앞서 사용한 중간조밀한 모래 (medium sand)와 중간단단한 점토 (medium clay)에 대하여 상기 세가지 방법을 적용한 결과이다. 예상했던 대로, 방법 3이 방법 2보다 작은 결과를 주었으나 이들의 차이는 매우 작은 것으로 나타났다. 한편, 방법 1은 모래에서는 거의 방법 2의 결과와 거의 일치하나 점토에서는 전 앵커질량에 걸쳐서 0.2 - 0.4 m 정도 작은 결과를 주는 것으로 나타났다. 위에서 제시된 Fig. 10-Fig. 14의 최대침투깊이는 방법 3에 의하여 계산된 것이다.
4. 결 론
주묘과정 중 발생하는 앵커의 지중침투는 말뚝 설치에서와 유사한 토체의 저항력을 받는다. 본 연구에서는 말뚝 침투의 역학적 특성을 참조하여 풀루크 앵커의 침투 예측을 위한 수치해석기법을 수립하였다. 토체의 저항력은 지지력 (bearing force)과 마찰력 (friction force)으로 구분되며 풀루크와 생크 그리고 계류체인의 각각에 대해서 산정하였다. 세부 결론은 다음과 같다.
- Stevin MK3 앵커에 대한 Vryhof (2015) 도표의 값 (침투깊이, 극한파주력, 견인거리)들을 이용하여 저항력 계수들을 보정한 결과, 풀루크와 생크는 연속보에 작용하는 지지력과 마찰력 계수를 적용하는 것이 도표 값들과 비교적 유사한 결과를 주는 것으로 나타났다. 그러나, 일종의 강체인 풀루크 및 생크와는 달리 유연한 계류체인에 작용하는 단위길이당 저항력은 단일말뚝의 성향을 보이며 연직말뚝의 지지력 및 마찰력 계수를 적용하는 것이 바람직한 것으로 나타났다.
- 2.1톤 앵커에 대한 수치해석을 중간느슨한 모래 (medium sand)와 중간단단한 점토 (medium clay)에 각각 적용한 결과, 침투가 진행되면서 역 캐티너리 형상의 계류체인과 그리고 플루크 하면의 경사각이 영으로 수렴하는 괘적을 잘 보여주었다. 괘적에서 도출한 극한 침투깊이는 (풀루크 하면 경사각 = 0)의 조건으로부터 직접적으로 구한 값들과 잘 일치하였다.
- 앵커 침투는 앵커 및 체인의 기학학적 형상, 앵커 중량, 토질 특성 등에 따라 달라진다. 따라서, 케이블의 적정 매설심도 산정은 임의 관심해역에서의 대표적 앵커와 해당 토질조건에 대하여 본 수치해석을 적용하여 계산한 앵커의 극한 침투깊이를 고려하여 설정할 수 있다.
본 수치해석과 더불어 실 스케일 앵커의 주묘실험이 수행되었으며 추후 실험결과를 이용한 수치해석의 추가적인 보정이 이루어질 계획이다. 보정 후 스톡앵커와 스톡리스 앵커의 질량, 그리고 토질조건의 변화에 따른 침투깊이의 변화를 독취할 수 있는 설계도표를 생성할 계획이다. 그 결과는 추후 후속 논문에서 소개할 계획이다.
감사의 글
본 논문은 2022년도 한국전력 전력연구원의 ‘해저케이블 보호설비의 설계기준 및 수치해석기술 개발’과제의 지원으로 수행된 연구임.