지반스프링 모델을 활용한 점성토 지반에서 석션앵커의 파주력 고찰
Holding Capacity of Suction Anchor in Cohesive Soils based on Soil-Spring Model
Article information
Trans Abstract
In this paper, a soil-spring model was applied to evaluate the holding capacity according to the loading position of the suction anchor. The API(2010) method, which is mainly applied to small-diameter piles, the PISA(2015) method, which recently introduced research results in offshore wind power design, and the Jeanjean(2009) method, which was presented as a model suitable for large-diameter piles in cohesive soil, were analyzed. A comparative review of the finite element analysis(ALE) was applied was performed for the conditions. A procedure for calculating the holding capacities for each loading position of the suction anchor was established using the soil-spring model, and it was confirmed that it was a method that could be used practically. When the soil-spring model of Jeanjean(2009) was applied, the results (5~10%) most similar to the FEM(ALE) analysis results in tendency and holding capacity could be obtained.
1. 서 론
석션앵커는 앵커 내부의 물을 배출(석션)하여 앵커체를 지중에 관입하여 설치하는 앵커를 의미하며, 보통 원통형의 말뚝의 형태를 가진다. 앵커 내부의 물을 외부로 배출하면서 발생하는 지반의 저항력 감소 효과와 내부와 외부의 압력 차이로 인해 발생하는 관입력으로 쉽게 설치할 수 있어, 수압의 차를 크게 이용할 수 있는 깊은 수심에서 매우 효과적이기 때문에 석유 및 가스 채광을 위한 대형 부유식 플랜트의 계류앵커로 많이 사용되어 왔다. 석션앵커는 대구경의 말뚝과 외형은 같지만, 말뚝과 다르게 하중이 작용하는 위치는 앵커의 상단뿐만 아니라, 중간 또는 하단과 같이 계류체인을 연결하는 위치를 다양하게 적용하고 있는데, 동일한 석션앵커에서 재하위치에 따라 발휘하는 파주력이 달라지기 때문이다. 가장 큰 파주력을 발휘할 수 있는 위치를 찾는 것이 매우 중요하며, 이를 위해서는 앵커와 체인의 연결부인 패드아이의 위치에 따른 앵커의 파주력 변화를 평가할 수 있어야 한다.
이 논문에서는 석션앵커의 파주력을 평가하는 방법 가운데 지반스프링 모델을 적용하였는데, 최근 해상 풍력 하부구조의 설계에서 통합하중해석을 위해 지반스프링 모델을 적용하고 있어, 고정식뿐만 아니라 계류앵커가 적용되는 부유식 풍력구조물의 설계에서도 동일하게 사용할 수 있는 지반스프링 모델을 비교 검토하였다. 그러나 지반스프링 모델은 말뚝의 상단에 하중이 작용할 때, 횡방향 변위와 하중의 거동을 분석하기 위해 사용되어 왔지만, 말뚝의 중간 위치 또는 하단에 하중이 작용할 때의 변위 거동을 평가하기 위해 사용된 사례는 전무하다. 여기에서는 다양한 지반스프링 모델을 적용하여 앵커에 재하위치에 따른 파주력을 산정하고 유한요소해석결과와 비교하여, 석션앵커에서 재하위치에 따라 파주력을 가장 유사하게 도출하는 지반스프링 모델을 제안하고자 한다.
2. 지반스프링 모델
2.1 개요
횡방향 하중을 받는 말뚝기초의 거동을 평가하는 방법은 한계상태를 가정하여 힘과 모멘트의 평형조건에 따라 평가하는 극한평형법(limit equilibrium method)과 지반을 탄성체로 가정하여 반력을 평가하는 지반반력법, 지반을 여러 개의 비선형 스프링으로 가정하여 말뚝의 거동을 평가하는 지반스프링 방법 그리고 유한요소해석 등이 있다. 현장에서 횡방향 재하시험을 수행하여 엄밀하게 평가하는 방법이 가장 정확하지만, 많은 비용이 소요될 뿐만 아니라 현장여건이 허락하지 않는 경우도 있어 사례가 많지 않으며, 일반적으로 유한요소해석이 정확도가 높은 방법으로 평가되고 있다. 다만 해석의 간편성을 이유로 극한평형법과 지반스프링 방법이 많이 사용되고 있다. A.G.(2001), Bang et al. (2001), DNV(2005), Murff et al.(1993)은 점성토 지반에서 석션앵커의 파주력을 극한평형법으로 평가하는 방법을 제시하고 있다. 한편, 최근 해상 풍력 설계에서 지반스프링 모델이 통합하중해석에 적용되면서, 횡방향 저항력을 평가할 수 있는 지반스프링 모델에 대한 연구가 활발히 이루어지고 있다(Burd et al., 2020; Byrne et al., 2015; Byrne et al., 2017; Byrne et al., 2020). 이를 통해 해상 풍력 하부구조물인 모노파일(monopile)이나 대구경 말뚝 등 설계기법에 적용된 바 있다. 그러나 기존에는 직경대비 높이가 긴 말뚝을 대상으로 하였는데, 석션앵커의 경우 지름이 크고 길이가 짧으므로 이에 대한 지반스프링 모델이 필요하다.
2.2 소구경 말뚝에서 지반스프링 모델
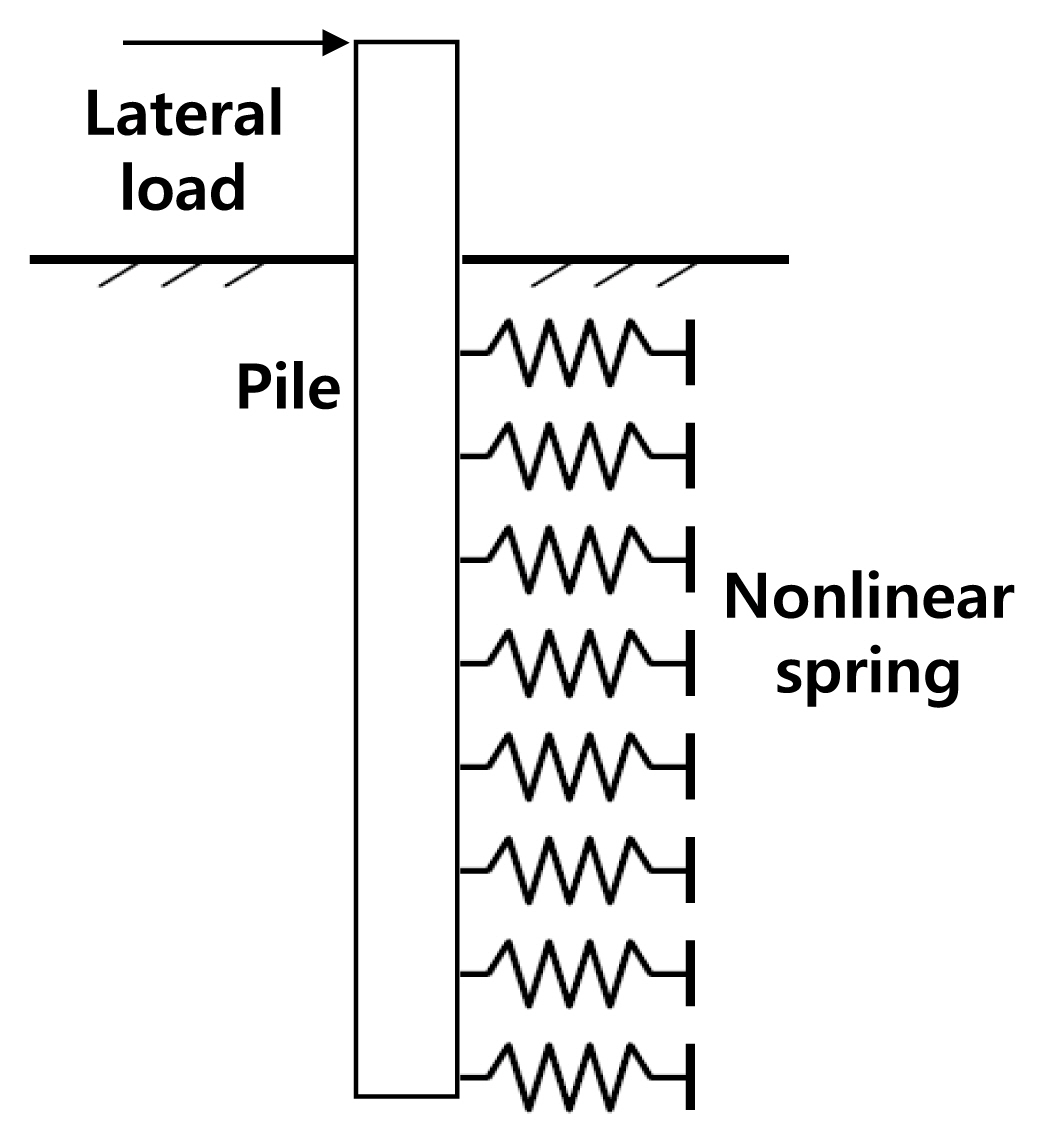
지반스프링 모델은 Fig. 1과 같이 지반을 횡방향 비선형 스프링으로 모사하여 횡방향 하중을 받는 말뚝의 거동을 평가하는 방법이다. 이 방법은 해석적 방법을 기반으로 하고 실험을 통해 많은 연구자들에 의해 연구가 진행되었다. API(2010)에는 연약한 점성토 지반에서는 Matlock(1970)의 횡방향 지반스프링 p-y 모델과 단단한 점성토 지반에서는 Reese et al.(1975) 제안식 그리고 사질토 지반에서는 O’Neill et al.(1983) 제안식이 사용되고 있다. Fig. 2는 대표적인 Matlock (1970)의 p-y스프링을 보여주고 있다.
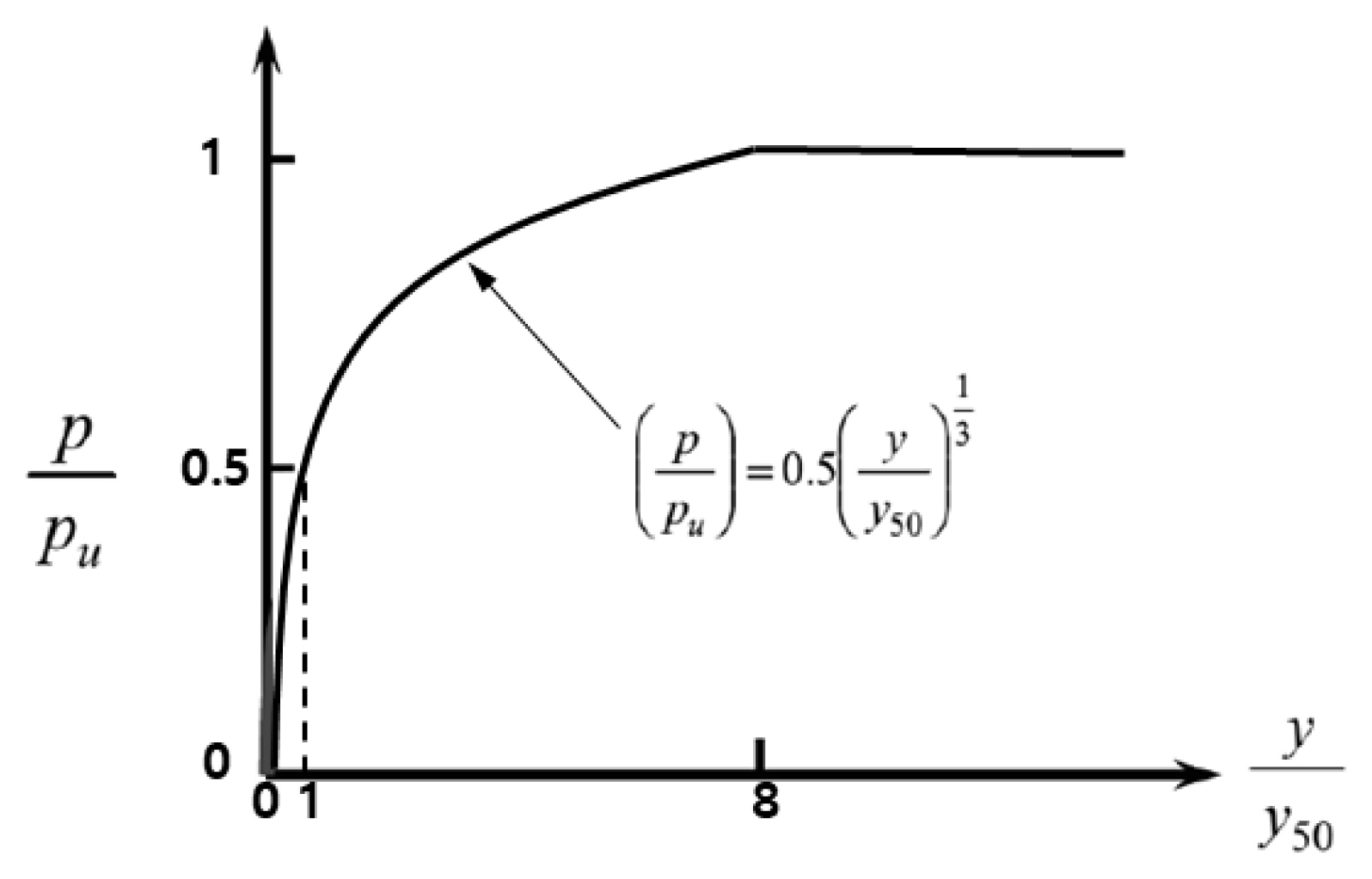
p-y spring model of clay(Matlock, 1970)
2.3 대구경 말뚝에서 지반스프링 모델
2.3.1 PISA(Pile Soil Analysis) 모델
일반적으로 석션앵커는 지름이 크고 길이가 말뚝기초에 비해 상대적으로 짧은데, API(2010)에서 제시하고 있는 p-y 스프링모델은 소구경의 긴 말뚝을 대상으로 얻어진 결과를 반영하고 있기 때문에 대구경 조건인 석션앵커에서는 그대로 적용할 수 없다. 대구경 말뚝에 대한 p-y 모델을 도출하기 위해 많은 연구자들이 다양한 방법을 제시하고 있는데, Lam et al.(1986)은 기존의 지반스프링 모델에 적용하고 있는 마찰저항 스프링인 t-z와 선단저항 스프링인 Q-z, 횡방향 스프링인 p-y에 추가적으로 말뚝의 지름이 커지면서 발생하는 말뚝저면에서 전단력과 모멘트 스프링을 추가할 것을 제시하였다.
해상 풍력의 구조물설계는 동적인 거동을 평가하여야 하며, 이를 위해 다양한 설계하중조건에 대해 통합하중해석을 수행하고 있는데, 이 때 말뚝이 설치되는 지반은 p-y 지반스프링으로 적용하고 있다. 그런데 해상 풍력발전 구조물의 기초로 사용되는 말뚝은 대부분 3m 이상의 대구경 조건이기 때문에, 앞 절에서 제시하고 있는 기존의 p-y 모델을 그대로 적용하는 것은 한계가 있다. 대구경 말뚝에 적합한 p-y 스프링의 모델을 도출하기 위해 Lam et al.(1986)은 기존의 p-y 스프링만으로는 정확한 평가가 불가능하기 때문에 말뚝 주면에서 모멘트 스프링과 저면에서 전단저항을 추가로 고려하여야 한다고 제안한 바 있고, 최근 해상풍력 기초 설계를 위해 수치해석과 원심모형시험, 현장재하시험의 결과를 바탕으로 Lam et al(1986) 모델을 개량하는 연구(PISA project)가 수행된 바 있다(Burd et al.(2020, Byrne et al.(2015), Byrne et al.(2017), Byrne et al.(2020)). Fig. 3은 Lam et al. (1986)과 PISA에서 사용하고 있는 지반스프링 모델의 개념을 나타낸 것으로, t-z 스프링과 Q-z 스프링, p-y 스프링에 모멘트 스프링인 m(z,θ), 말뚝 선단 저면에서 전단력(HB(vB))과 모멘트(MB(θB))를 추가하여 적용하고 있다.
2.3.2 Jeanjean(2006, 2009) 모델
점성토 지반에서 대구경 말뚝의 p-y 스프링 모델에 대해서도 많은 연구결과가 발표되고 있는데, Jeanjean(2006, 2009)은 원심모형시험의 결과를 활용하여 대구경 말뚝의 횡방향 저항력을 평가하는 방법을 제시하였다. 원심모형시험에서 얻어진 계수 Np를 활용하며, 지반의 전단탄성계수와 비배수 전단강도의 비를 활용한 p-y 관계식을 다음 식과 같이 제시하고 있다. 최근 점성토 지반에서 말뚝의 p-y 곡선으로 자주 활용되고 있다.
여기서,
Pmax = Np×su
Gmax: 전단탄성계수
su: 비배수 전단강도
y: 횡방향 변위
D: 말뚝의 지름
ξ = 0.25 + 0.05 × λ (λ<6)
ξ = 0.55(λ≥6)
su0: 지표면 비배수 전단강도
su1: 해당 깊이에서 비배수 전단강도z
z: 해당 깊이
2.4 재하위치에 따른 앵커의 파주력
많은 연구자들이 석션앵커의 재하위치에 따른 파주력을 평가한 결과가 있는데, Bang et al.(2001)에서는 극한평형법을 활용하고 있으며, Han et al.(2018)에서는 유한요소해석법을 활용한 방법을 활용하고 있다. 석션앵커뿐만 아니라 Na et al.(2013)는 지중에 설치되는 매입식 석션앵커(Embedded suction anchor)에 대해서 유한요소해석을 수행하여 재하위치, 재하각도별로 파주력을 평가하고 있다. 지반조건에 따라 다소 차이는 있지만, 점성토 지반에서는 앵커의 중앙에 하중이 가해질 때 가장 큰 파주력을 발휘하는 것으로 나타났다.
지반스프링은 주로 말뚝의 횡방향 지지력과 변위 특성을 평가하기 위해 사용되고 있으며, 지반스프링 모델을 이용하여 지중 임의의 위치에 하중을 가하여 석션앵커의 파주력을 평가한 사례는 보고된 바 없다. 이 논문에서는 다양한 지반스프링 모델을 적용하여 석션앵커에서의 하중재하위치를 변경하면서 해석을 수행하여, 지반스프링 모델에 따른 위치별 파주력을 산정하고 유한요소해석결과와 비교를 통해 석션앵커의 파주력 산정에 적합한 지반스프링 모델을 도출하고자 하였다.
2.5 PISA 방법에서 M-θ 스프링 모델의 제안
앞에서 설명한 PISA 방법에서는 말뚝 선단 저면에서 추가적인 반력들과 함께 말뚝 요소별 모멘트 스프링을 적용하는 것으로 제안되어 있으나, Burd et al.(2020), Byrne et al.(2015), Byrne et al.(2017), Byrne et al.(2020)의 논문에서는 Fig. 4와 같이 M-θ 스프링은 주면마찰력을 나타내는 t-z 곡선을 활용하는 것으로만 제시되어 있고 구체적인 적용방법에 대해서는 언급이 없다. 따라서 이 논문에서는 t-z 곡선을 활용하여 M-θ 스프링 모델을 도출하는 과정을 다음과 같이 유도하였다. 말뚝의 회전으로 인해 발생하는 모멘트를 평가하기 위해, 말뚝 주면에 작용하는 마찰저항(t)과 해당 위치에서 모멘트 길이를 활용한다.
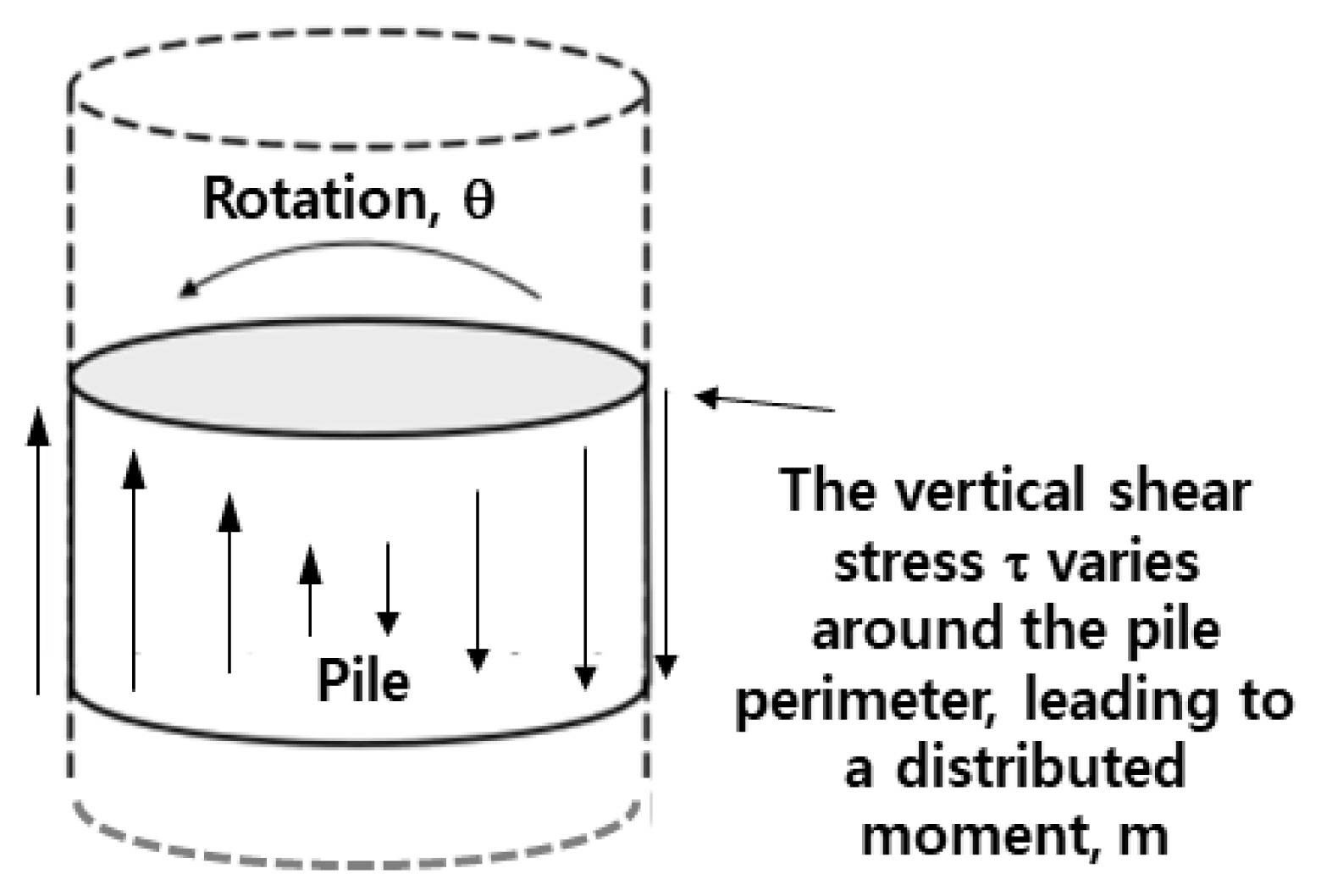
Moment spring concept(Byrne et al., 2015)
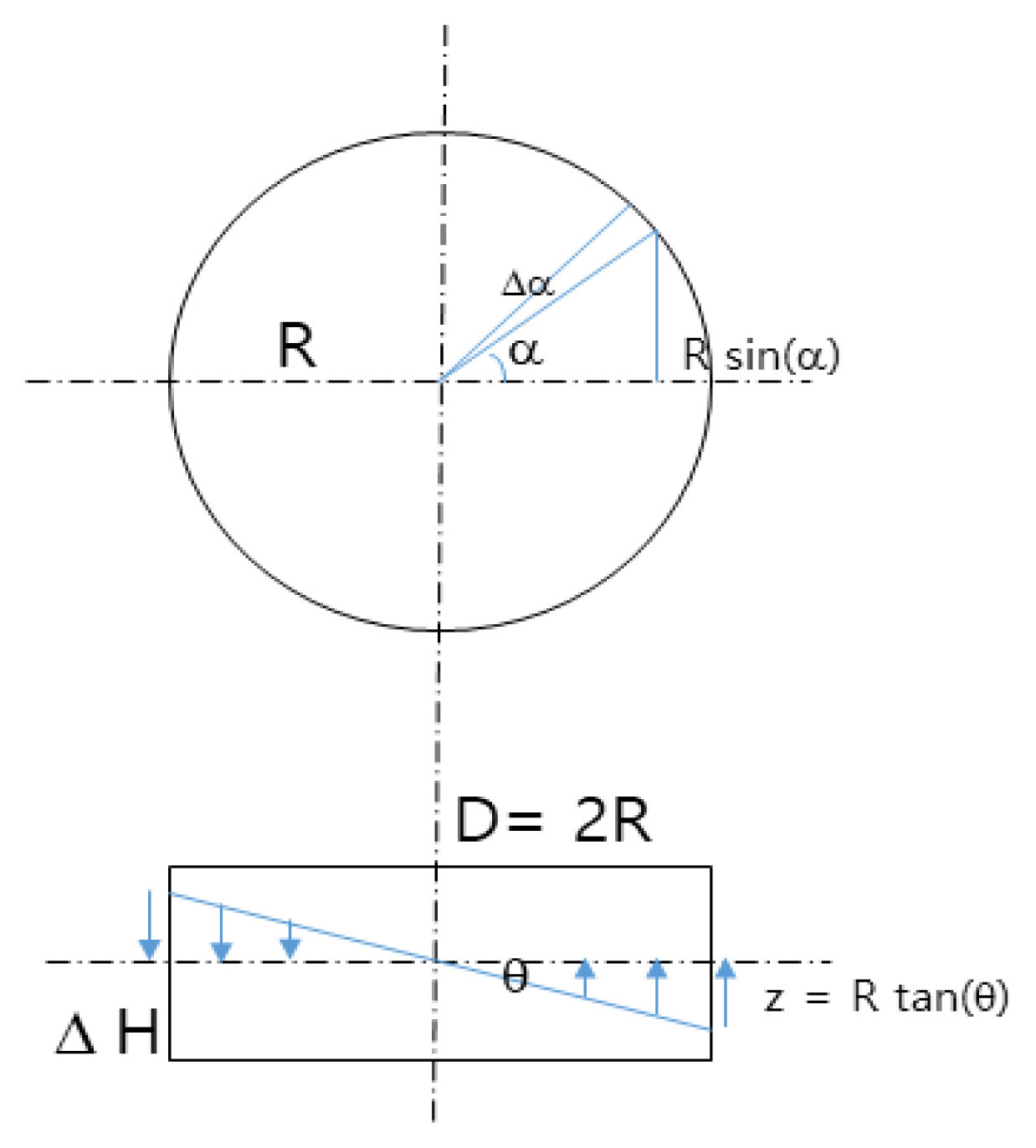
임의의 회전각을 θ로 두면, 연직변위 z는 Fig. 5와 같이 다음 식으로 정의할 수 있다.
여기서, R : 말뚝의 반지름
∆H: 말뚝요소의 두께
τ: 전단응력, τmax: 최대전단응력
t-z곡선에서 말뚝주면 평면의 임의 각도(α)에서 전단응력 tα 도출하고, 전체 각도에 대해 적분하며 다음과 같이 임의의 회전각 θ에서 모멘트를 얻을 수 있다.
3. 지반스프링 모델을 이용한 해석결과
3.1 개발 프로그램의 검증
지반스프링 모델의 해석을 위해 비선형 스프링 모델을 부착한 2차원 유한요소해석 프로그램을 제작하였다. Fig. 3과 같이 t-z, Q-z, p-y, m-θ 스프링과 선단 저면 전단력전단력(HB(vB))과 모멘트(MB(θB))를 노드별로 적용하고 탄성보(Timoshenko beam) 해석을 수행하는 프로그램으로 제작되었으며, Fig. 6과 Fig. 7과 같이 입력과 해석결과를 도출할 수 있다.
개발한 프로그램에는 API(2010)에서 제시하고 있는 점성토 지반에서 적용하는 Matlock(1970) 모델과 사질토 지반에서 적용하는 O’Neill et al.(1983) 모델과 Jeanjean(2009) 모델, PISA 모델을 활용할 수 있도록 제작되었다. 제작된 프로그램의 검증을 위하여 p-y 모델에 대한 상용 소프트웨어인 LPILE (Reese, 1987)을 활용하여 동일한 예제에 대해 비교검토를 수행하였다. LPILE에서는 지반스프링을 적용하여 말뚝의 횡방향 거동을 평가할 수 있으며, 기존의 많은 연구사례를 통해 검증이 이루어져 있고, 이 연구에서 개발한 지반스프링 적용 알고리즘이 정확하게 코딩이 되었는지를 검증하기 위해 같은 조건으로 해석을 수행하여 비교하였다.
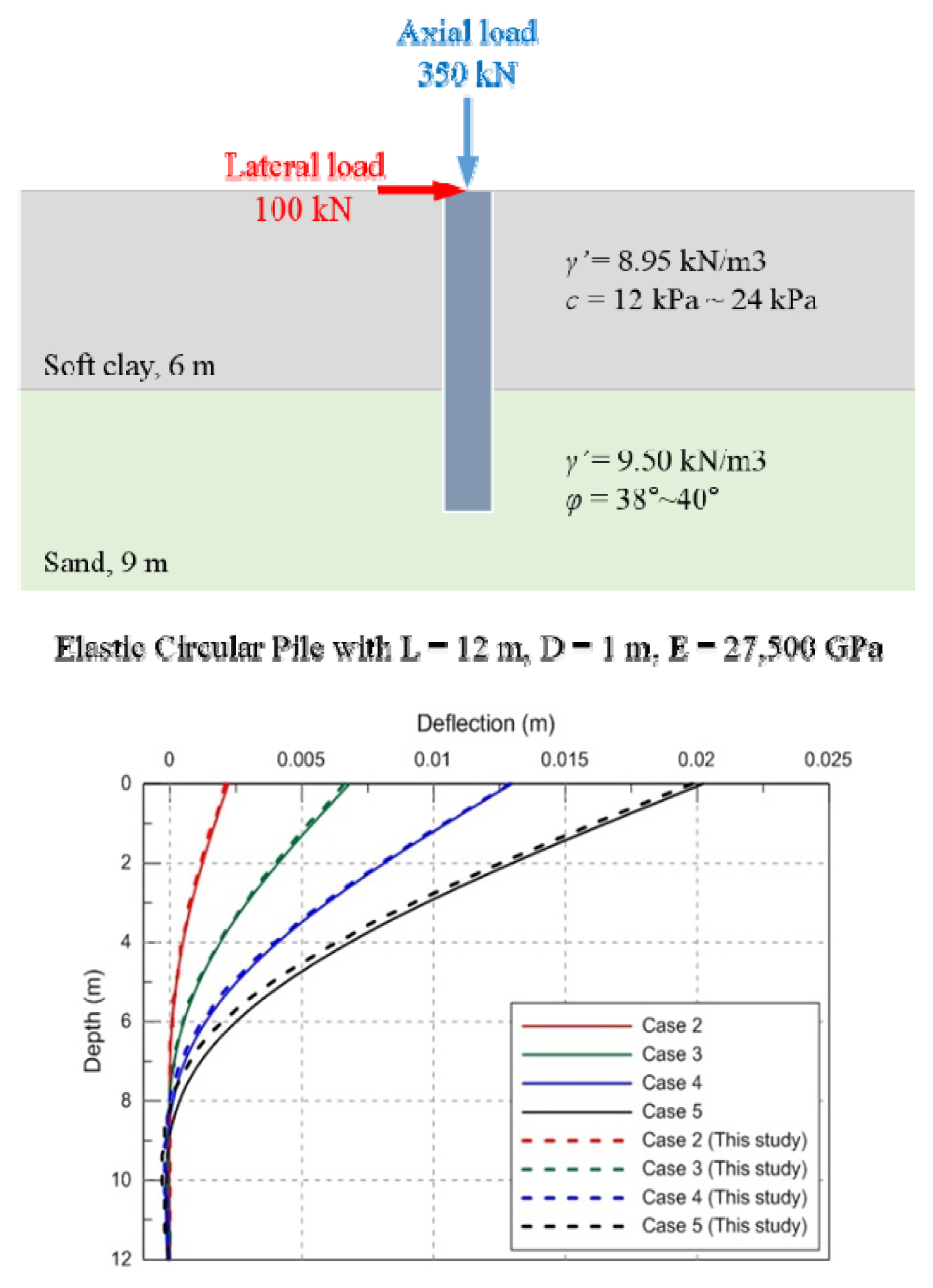
적용 예제는 Fig. 8과 같으며, 하부 사질토층과 상부 점성토층 조건이며, API(2010) 지반스프링 모델을 적용하였다. 그림에서 하중의 크기에 따라 Case 2~Case 5로 구분하고, LPILE의 해석결과와 연구에서 개발된 프로그램의 계산결과를 비교한 결과 유사한 값과 경향을 보임을 확인할 수 있다.
3.2 해석 조건
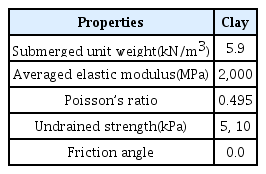
개발된 프로그램을 활용하여 다음 Table 1에서 제시된 석션앵커를 비배수 전단강도가 5kPa과 10kPa인 점성토 지반에 설치하여, 하중재하위치를 앵커 상단(Top), 상단에서 1/3위치, 1/2위치, 2/3위치, 하단(Bottom)으로 구분하여 적용하였다.
이 논문에서는 지반스프링 모델을 API(2010) 기준에 수록된 Matlock(1970) 모델과 여기에 말뚝 선단 저면의 반력과 모멘트 그리고 회전각-모멘트 스프링이 추가된 API+PISA 모델, 점성토 지반에서 대구경말뚝에서 많이 사용되는 Jeanjean (2009) 모델과 여기에 PISA방법과 같은 지반스프링을 추가한 경우를 비교 대상으로 하였다.
3.3 비교를 위한 유한요소해석
지반스프링 모델을 적용하여 석션앵커의 파주력을 평가한 결과와 비교를 위하여 유한요소해석을 수행하였다. 수치해석은 범용 유한요소해석 프로그램인 ABAQUS(Dassault, 2010)를 활용하였으며, ABAQUS는 구조, 지반, 수리 등 다양한 해석모델을 탑재하고 있고, 특히 지반해석에서 발생할 수 있는 대변형 조건에 대한 해석기법을 탑재하고 있는데, 여기에서는 표준(Standard) 해석방법과 ALE(Arbitrary Lagrangian Eulerian)의 Adaptive Meshing 기법을 적용하였다. ALE 기법은 유한요소해석에 발생할 수 있는 대변형으로 인한 요소망의 왜곡문제를 해결하기 위해 요소망을 변형과정에서 재배열(re-meshing)하는 방법이다(Dassault System, 2010). 석션앵커의 경우에는 앵커 중간 또는 하단에서 하중을 가할 때 회전이 발생하면서 요소망의 변형이 커지므로 ALE 방법을 적용하지 않으면 지반의 반력이 상대적으로 크게 평가되는 문제가 발생할 수 있다(Na et al., 2013). 지반조건은 앞절과 동일하며, 유한요소해석을 위해 Table 2에서 추가적인 입력변수를 제시하였다.
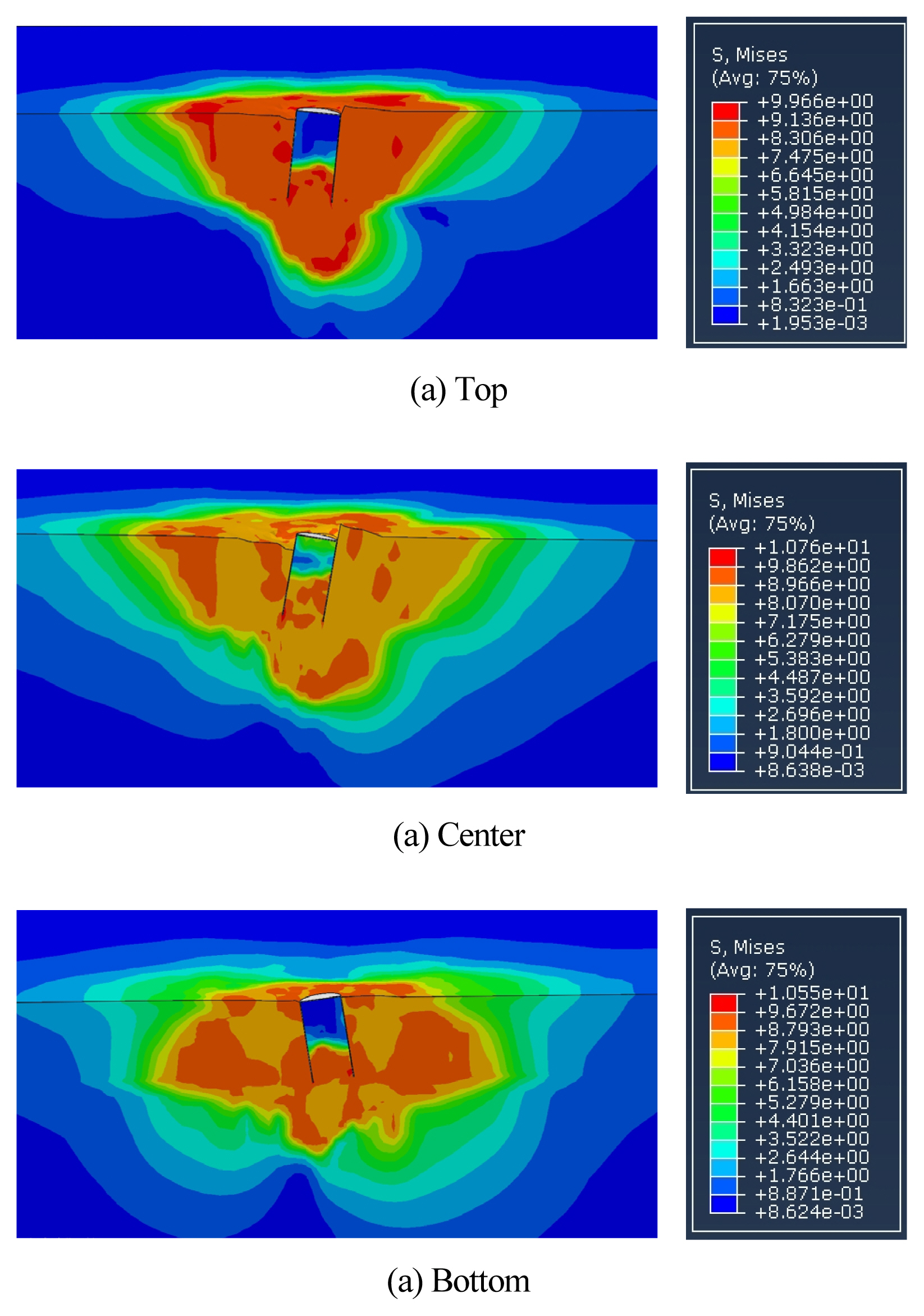
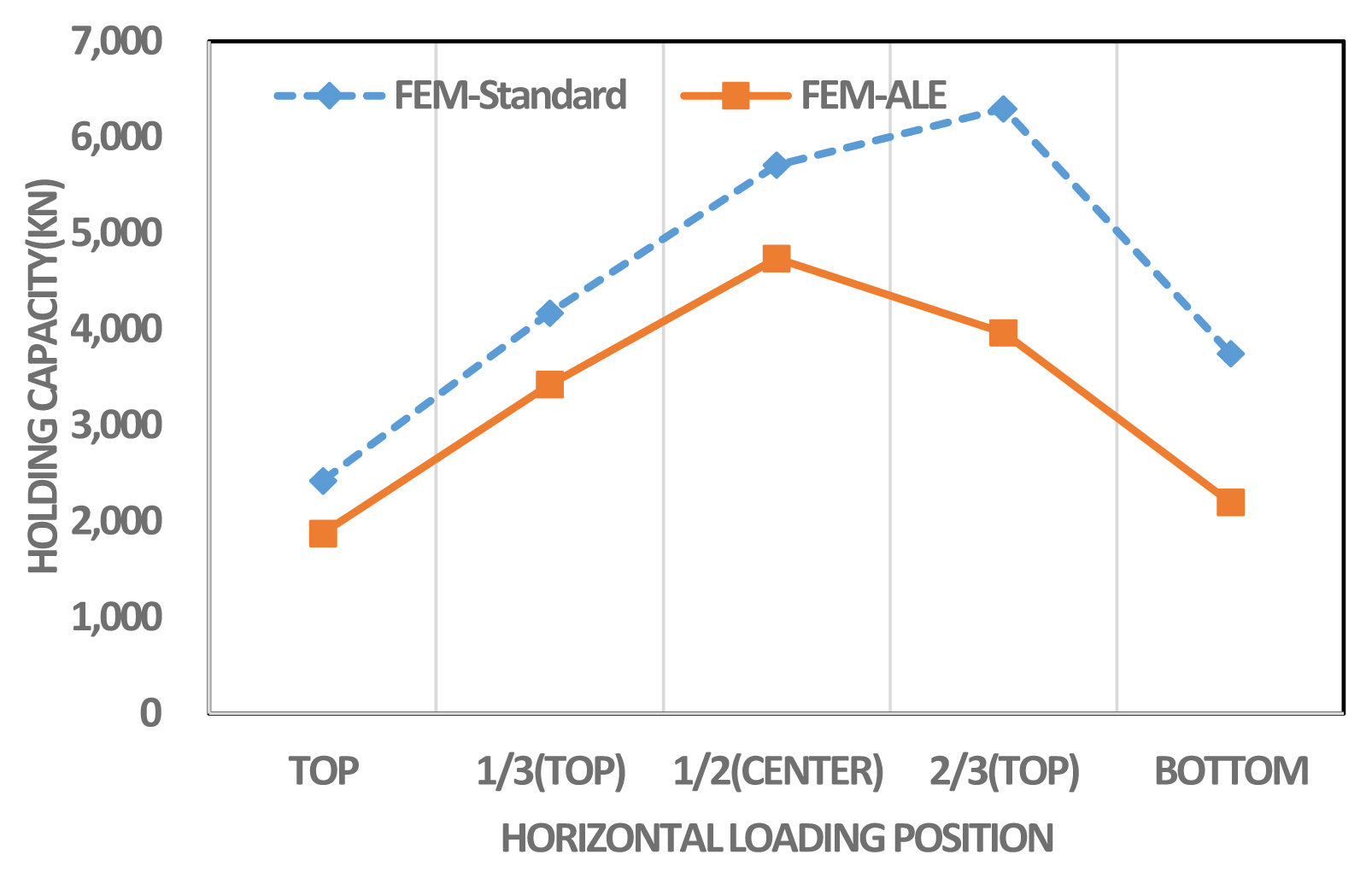
다음 Fig. 9는 유한요소 해석결과 가운데, 비배수 전단강도 5kPa 조건에서 앵커 상단과 1/2, 하단 위치에서 하중을 가하였을 때의 응력분포를 나타낸 것이다. Fig. 10은 유한요소해석의 Standard 해석결과와 ALE 해석결과를 비교한 것으로, 재하위치와 해석방법에 따른 파주력의 크기를 보여준다. 석션앵커의 상단에서 가장 작은 파주력이 나타나며, 중간위치에서 증가했다가 하단위치에서 다시 작아지는 경향은 동일하지만, Standard 해석이 앵커하단에 하중이 가해졌을 때 요소망의 왜곡의 영향이 커지기 때문에 ALE해석보다 큰 값을 보이고 있다. 이것은 ALE 기법을 적용한 Na et al.(2013), Han et al(2018)의 연구와 유사한 경향이다.
3.4 해석결과 비교
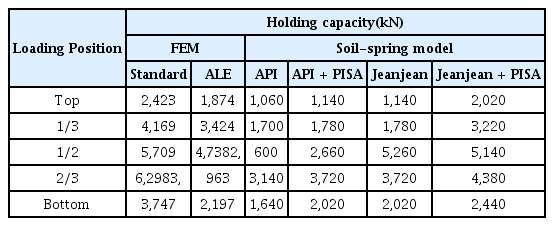
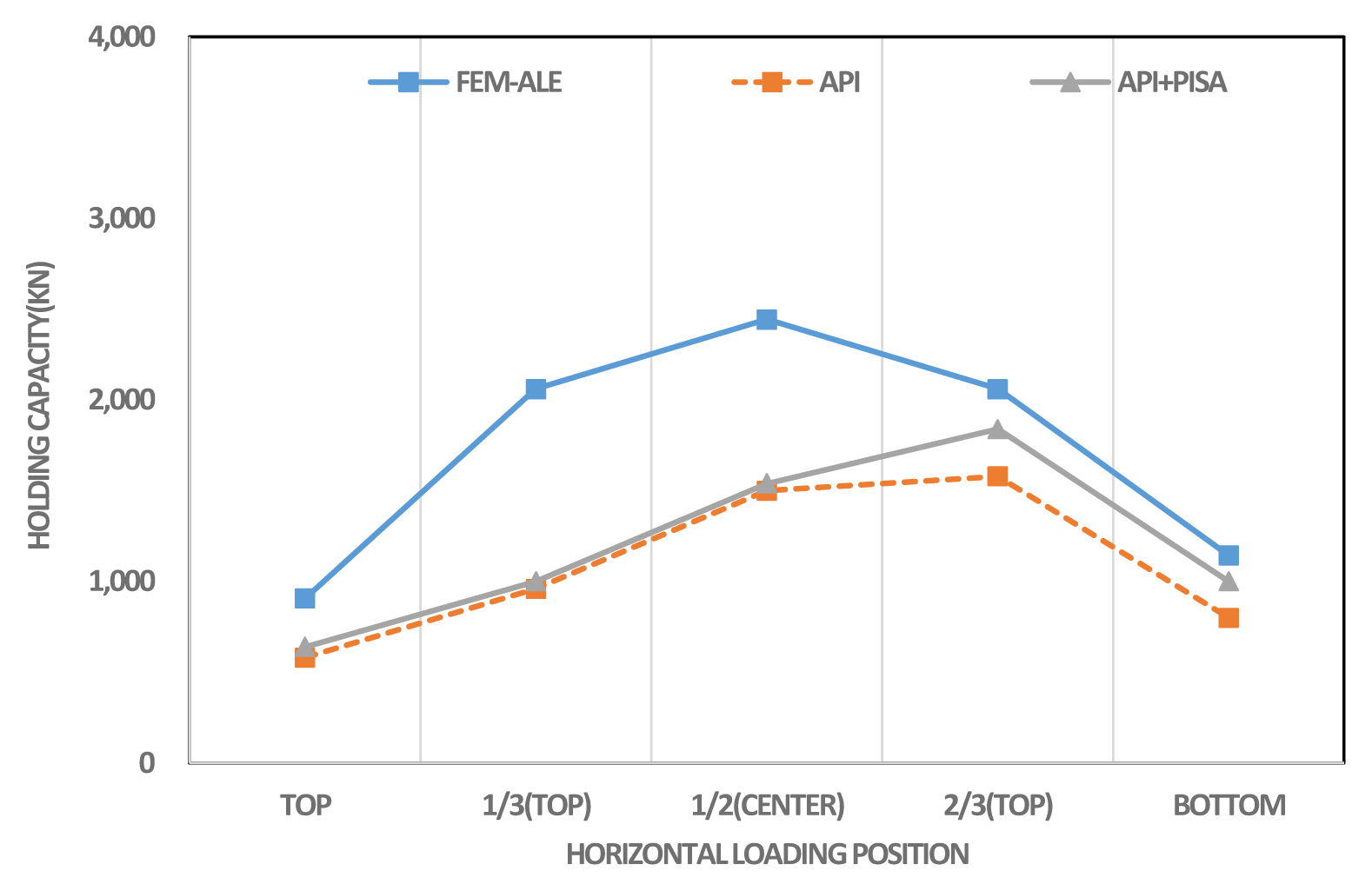
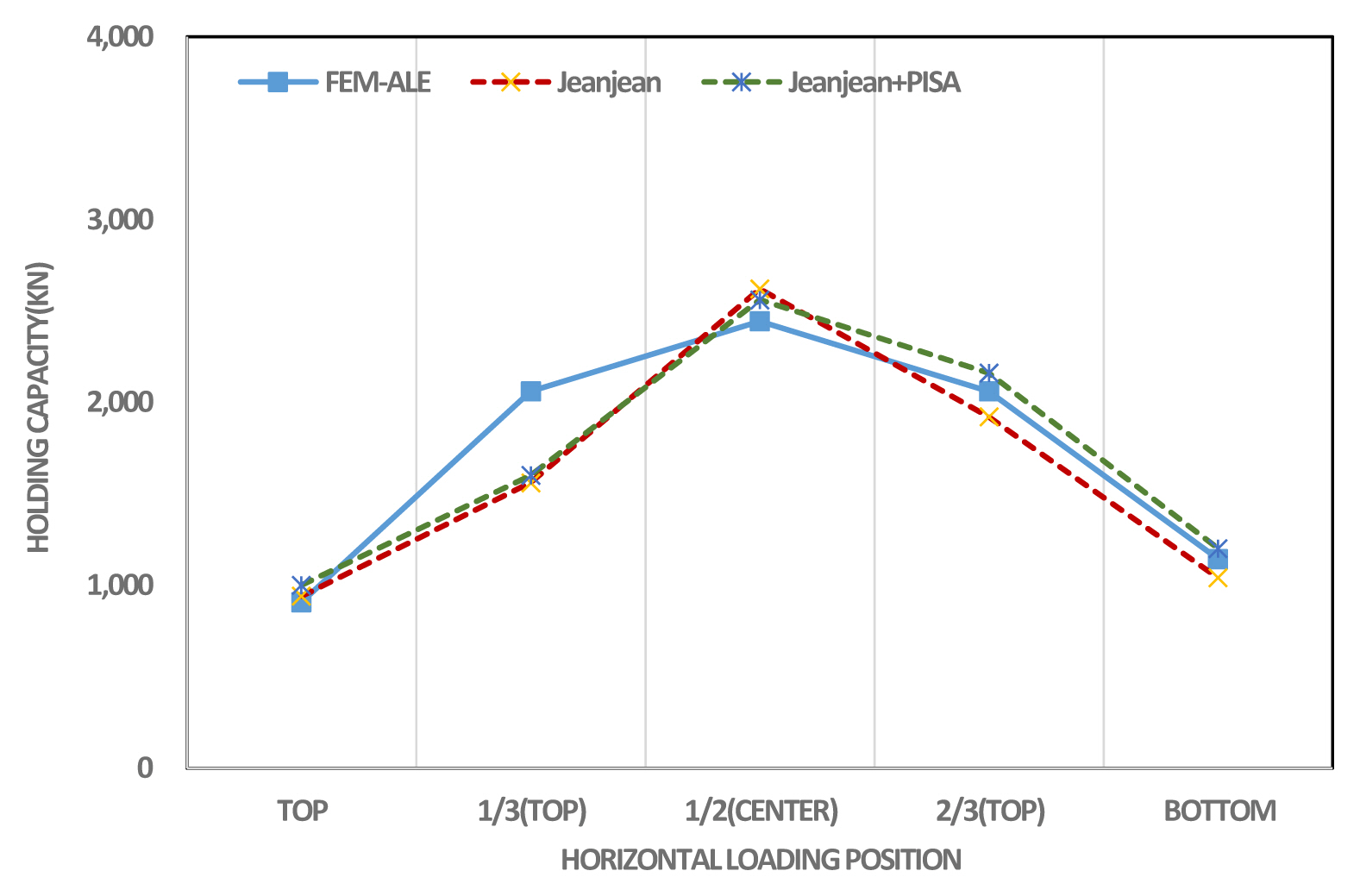
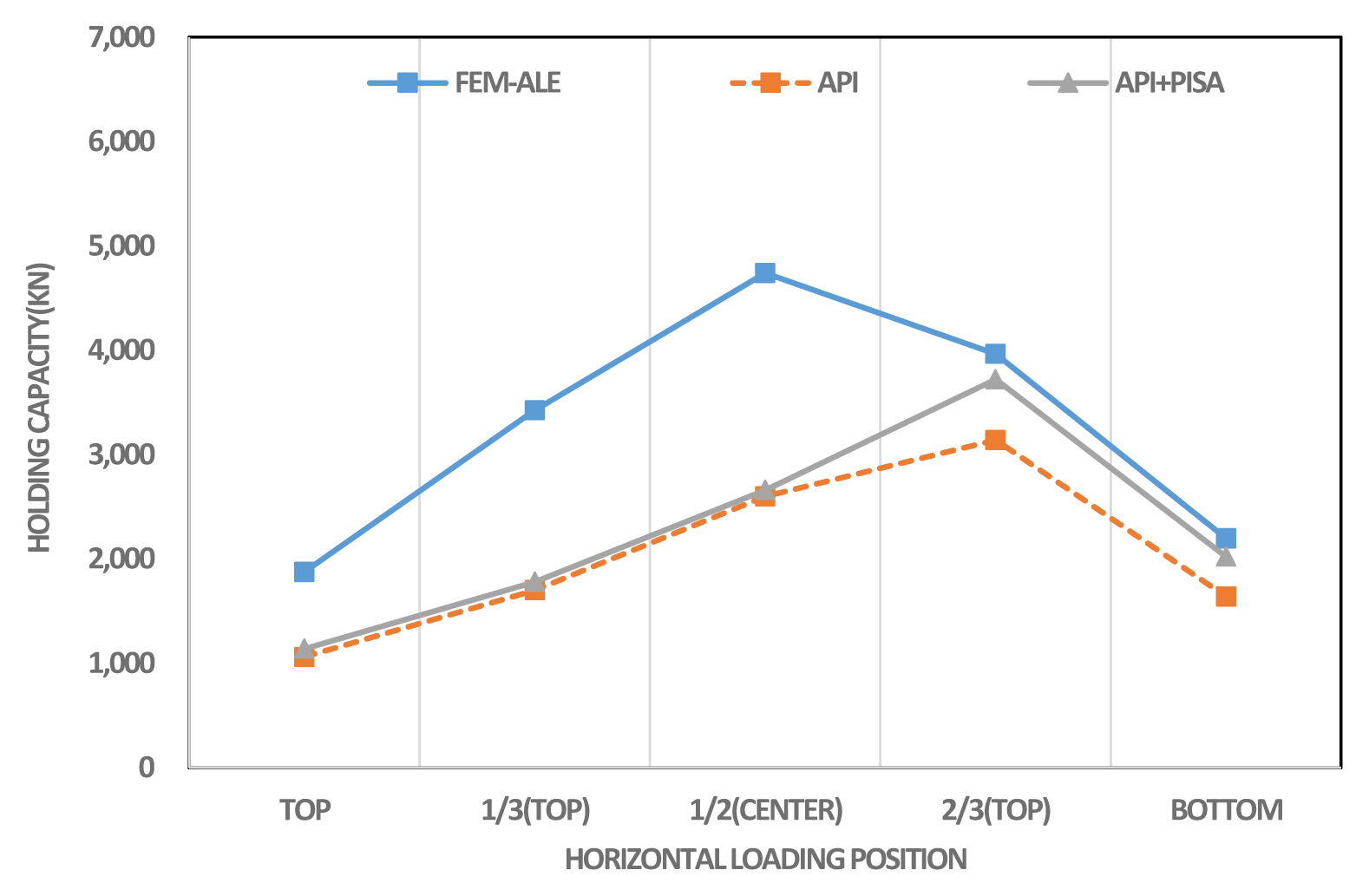
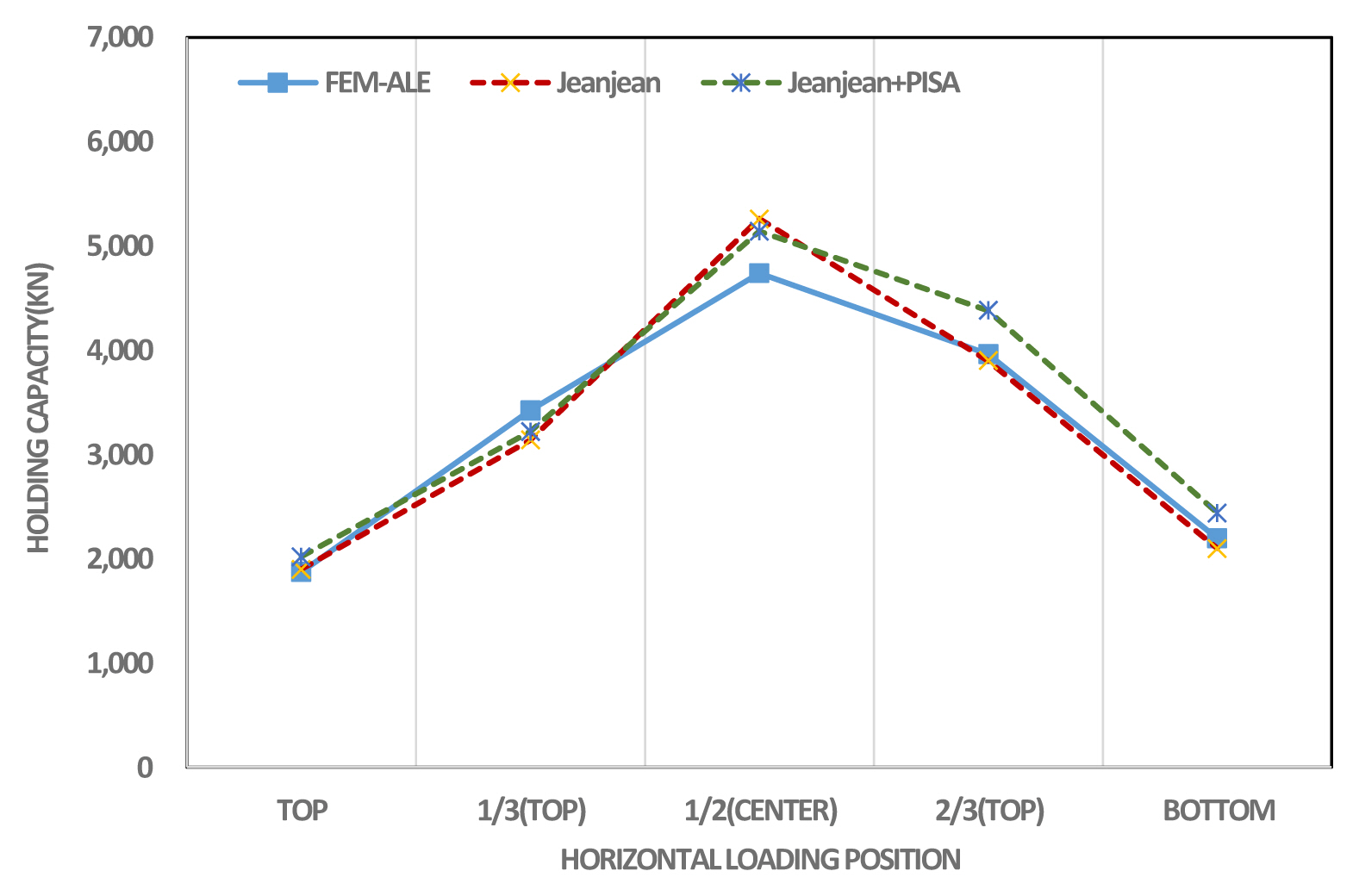
지반스프링 모델을 적용하여 해석한 결과와 유한요소해석을 비배수 전단강도 5kPa, 10kPa인 경우에 대해 Table 3과 Table 4에 각각 제시하였다. 또한 Fig. 11과 Fig. 12에서는 비배수 전단강도 5kPa 조건에서 지반스프링 모델의 결과와 FEM-ALE 해석결과와 비교하여 도시하였는데, Fig. 11은 API 방법과 API+PISA방법을 비교한 것이고, Fig. 12는 Jeanjean 방법과 Jeanjean+PISA 방법을 비교한 것이다. Fig. 13과 Fig. 14는 비배수 전단강도 10kPa인 조건에 대한 동일한 방법으로 비교한 결과이다. 비배수 전단강도의 크기에 따른 파주력은 표와 그림에서 알 수 있듯이 거의 유사한 경향을 보이고 있다.
앞 절에서 설명한 바와 같이 유한요소해석인 ALE 결과에서는 석션앵커의 상단에서 가장 작은 파주력이 산출되고, 1/2위치에서 가장 큰 파주력이 산출되었는데, API 방법과 API+PISA 방법에서는 앵커의 2/3 위치에서 가장 큰 파주력을 보이고 있다. 또한 석션앵커의 상단과 하단에 하중이 가해질 경우에는 어느 정도 유사한 파주력이 나타지만, 1/3, 1/2 위치에서는 상당한 차이를 보이고 있다. 이것은 기존의 p-y 스프링 모델은 말뚝 상단에서 작용하는 횡방향 하중에 대해 검증이 이루어진 반면 재하위치가 중간인 경우에는 아직 충분한 검증이 이루어지지 않았고, 여기에서는 잘 맞지 않는 모델인 것으로 판단된다.
반면, Jeanjean 모델은 Fig. 12와 Fig. 14와 같이 석션앵커의 재하위치에 따른 파주력의 경향성과 유사하며, 크기도 위치별 파주력의 오차의 평균이 5kPa에서 10%, 10kPa에서 5%의 오차를 보이고 있다. Jeanjean의 지반스프링 모델은 석션앵커의 위치별 파주력 산정에 유한요소 해석결과와 유사한 결과를 보임을 확인할 수 있다. PISA 스프링이 적용된 경우를 보면, API 방법이나 Jeanjean 방법 모두에서 파주력의 크기가 크게 증가하지는 않는 것으로 평가되었다.
4. 결 론
이 논문에서는 석션앵커의 재하위치에 따른 파주력을 평가하기 위해 지반스프링 모델을 적용하였다. 기존 지반스프링 모델은 말뚝 상단에 횡방향 하중이 작용했을 때의 말뚝의 거동을 평가하기 위해 사용되었으나, 앵커에서는 하중 작용위치가 중간과 하단에 작용할 수 있기 때문에 작용위치에 따라 지반스프링 모델의 적용성에 대해 검토를 수행하였다. 지반스프링 모델은 소구경 말뚝에 주로 사용하고 있는 API(2010) 모델과 최근 해상풍력 설계를 위해 도입된 PISA(2015) 모델 그리고 점성토에서 대구경 말뚝에 적합한 방법인 Jeanjean(2009) 모델을 적용하여 해석을 수행하였으며, 비교를 위하여 동일한 조건에서 ALE 기법을 적용한 유한요소해석을 수행하여 다음과 같은 결론을 도출하였다.
(1) 지반스프링 모델을 이용하여 석션앵커의 재하위치별 파주력을 산정한 절차를 수립하였으며, 유한요소해석결과와 비교를 통해 실용적으로 활용할 수 있는 방법임을 확인하였다.
(2) API(2010)의 Matlock(1970) 방법에 의한 파주력 산정 결과, 재하위치가 상단에서 가장 작게 산출되었으며, 2/3 위치에서 가장 큰 파주력이 산출되었다. Jeanjean (2009) 방법과 FEM-ALE 해석결과에서는 1/2 지점에서 가장 큰 파주력이 산출되었다.
(3) Jeanjean(2009) 지반스프링 모델을 적용하였을 때, FEM-ALE 해석결과와 경향성과 파주력이 가장 유사한 결과(5~10%)를 얻을 수 있어, 석션앵커의 재하위치별 파주력 평가에 적용할 지반스프링 모델로 적합함을 확인하였다.
(4) 말뚝 선단 저면의 반력과 모멘트, 말뚝의 회전각과 모멘트 스프링을 추가로 적용하는 PISA(2015) 방법에서는 기존 방법에 비해 파주력을 크게 평가하지만 큰 영향을 받지는 않는 것으로 나타났다.
감사의 글
이 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20213030020200).